§ 5. Параметры взаимодействия

В реальных металлургических процессах химические превращения, как правило, происходят в многокомпонентных растворах. Например, стальная ванна является раствором многих неметаллов (С, S, Р, О, Н, N), а также легирующих элементов (Si, Mn, Cr и т.д.) в жидком железе.

Химический потенциал каждого компонента и, следовательно, его активность в таких растворах определяются не только его концентрацией, но и концентрациями и свойствами всех других растворенных веществ. Это необходимо учитывать при расчетах равновесий. Например, активность серы, растворенной в жидком железе, зависит от содержания в нем углерода, кремния и т.д. Присутствие С и Si увеличивает коэффициент активности серы и, следовательно, способствует десульфурации стали, присутствие марганца уменьшает активность серы. Протекание процесса выделения (или растворения) карбидных или нитридных фаз при термической обработке стали определяется при данной температуре активностями металлов образующих эти фазы, которые, в свою очередь, зависят от концентрации остальных компонентов твердого раствора. Для упрощения описания равновесий в подобных системах К. Вагнером и Д. Чипманом были введены, так называемые, параметры взаимодействия

Разложение логарифма коэффициента активности растворенного вещества, например, второго, в ряд Тейлора по степеням молярных долей компонентов для разбавленных растворов, где молярная доля растворителя х₁ близка к единице, дает:

150

(VI.21)

Из этого уравнения следует, что при x₃ = 0, x₄ = 0... и x₂ → 0 ln f₂, т.е. f

0

2

  является предельным значением коэффициента активности вещества 2 в чистом растворителе (постоянная величина) и этот бинарный раствор (1-2) подчиняется закону Генри.

При обычных практических расчетах можно ограничиться в уравнении (VI.21) лишь членами первого порядка. Производные, входящие в эти члены, называются параметрами взаимодействия (первого порядка). Они обозначаются следующим образом:

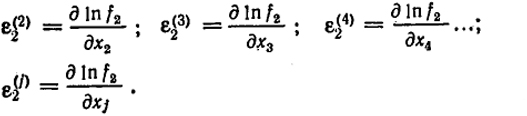
При этом уравнение (VI.21) упрощается, т.е.

lnf₂ (x₂, x₃, х₄...) = lnf

0

2

  + ε

(2)

2

  х₂ + ε

(3)

2

  х₃ + ε

(4)

2

  x₄ + ... + ε

(i)

2

  x_j. (VI.22)

В этом приближении логарифм коэффициента активности растворенного вещества 2 является линейной функцией концентраций остальных компонентов. Параметр ε

(2)

2

  характеризует зависимость коэффициента активности компонента 2 от его собственной концентрации, а параметры ε

(3)

2

  , ε

(4)

2

  ... - соответственно от концентраций других растворенных веществ.

Из уравнения (VI.22) следует, что при x₃ = x₄ = ... = 0 , подобным же образом x₂ = x₄... = 0

Отсюда следует, что

151

Сумма двух первых членов правой части этого уравнения равна lnf₂(x₂, x₃ = 0, x₄ = 0...). Обозначив отношения ^f(2)i остальных членах уравнения через f

(3)

2

  f

(4)

2

  , ..., найдем, что

f₂(x₂, x₃, x₄...) = f₂(x₂, x₃ = 0, x₄ = 0...)f

(3)

2

  f

(4)

2

  . (VI.23)

Первый сомножитель правой части уравнения (VI.23) есть коэффициент активности компонента 2 в бинарном растворе 1-2 при концентрации х₂, а остальные в растворах 1-2-3, 1-2-4, в которых x₂ → 0 и т.д.

Очень важно, что между параметрами взаимодействия различных компонентов раствора существует вполне определенная связь. Она может быть найдена из определения парциальной энергии Гиббса G_i = (∂G/∂n_i)_{j(j ≠ i)}. Последовательное дифференцирование парциальных молярных энергий Гиббса каких-либо двух компонентов раствора, например G₂ и G₃ по числам молей этих компонентов n₂ и n₃ приводит к двум соотношениям:

∂G2

∂n3

  =

∂2G

∂n2∂n3

  и

∂G3

∂n2

  =

∂2G

∂n2∂n3

  ,

откуда

∂G2

∂n3

  =

∂G3

∂n2

  . Учитывая, что G_i = G

0

i

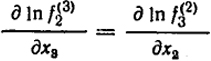
  + RT ln x_if_i, получим , откуда ε

(3)

2

  = ε

(2)

3

  или в общем виде ε

(j)

i

  = ε

(4)

2

  ... .

Уравнения (VI.22) и (VI.23) упрощаются при выборе в качестве состояния сравнения разбавленного раствора, для которого предельный коэффициент активности f

0

2

  (для компонента 2) равен единице. В этом случае:

(VI.24) (VI.25)

Вклад каждого из компонентов раствора, например j, в величину коэффициента активности компонента 2 согласно уравнению (VI.24) составляет

ln f

(j)

2

  = ε

(j)

2

  x_j. (VI.26)

Как отмечалось, для разбавленных растворов величины концентраций, выраженных в любых единицах, пропорциональны между собой. Поэтому уравнения (VI.24) и (VI.25)

152

справедливы, если концентрации выражены, например, в массовых содержаниях, %.

Поэтому численные значения величин ε_i будут другими.

153