Первый закон термодинамики является частным случаем общего закона сохранения энергии в применении к тепловым (термическим) явлениям. При рассмотрении балансов термических процессов необходимо учитывать работу, возникающую вследствие изменения объема системы.
Пусть какое-либо тело занимает объем V при давлении р, которое действует на поверхность тела S. При его расширении совершается механическая работа W. При бесконечно малом расширении тела поверхность, на которую действует давление, переместится на расстояние dl; бесконечно малое количество (порция) работы δW, совершаемой телом, определится уравнением
δW = pSdl.
(I.1)
Так как Sdl есть приращение объема тела dV, то
δW = pdV
(I.2)
Работа в неэлементарном (конечном) процессе равна сумме порций работ, и ее величина выражается определенным интегралом:
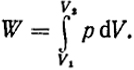 (I.3)
(I.3)
Следовательно, величина работы определяется площадью под кривой зависимости давления от объема при протекании того или иного процесса. Вид этой зависимости обусловлен характером процесса, поэтому работа при расширении тела от данного начального до данного конечного объема зависит от пути процесса.
На рис. 1.1 представлен случай, когда тело расширяется от объема V1 до объема V2 двумя различными путями. При этом величина работы в процессе I (горизонтальная штриховка) значительно отличается от соответствующей величины в процессе II (вертикальная штриховка).
Возникает вопрос, за счет какого источника происходит работа при расширении тел?
Пусть тело, например газ, помещено в теплонепроницаемый цилиндр с поршнем. Давление, оказываемое газом на поршень, уравновешено несколькими гирями. Если снять часть этих гирь, то газ расширится, и оставшиеся гири поднимутся на некоторую высоту, т.е. будет произведена работа. Из закона сохранения энергии вытекает, что единственным источником этой работы является сам
14
газ. Мы видим, что даже этот простой пример требует введения понятия о внутренней энергии U. Можно сказать, что газ произвел работу за счет уменьшения своей внутренней энергии (в рассматриваемом опыте газ после совершения работы мог охладиться). Очевидно, все тела
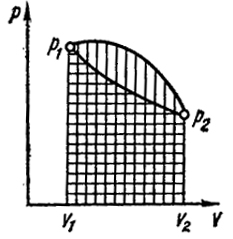
Рис. I.1. Зависимость работы от пути процесса
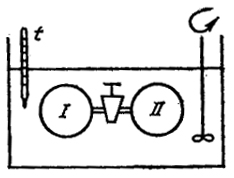
Рис. I.2. Схема опыта Джоуля
обладают определенным запасом внутренней энергии при заданных значениях параметров.
Уже отмечалось, что основные понятия термодинамики сложились до создания современной молекулярной теории вещества. Поэтому классическая термодинамика не занималась вопросом о природе внутренней энергии. В действительности эта энергия имеет молекулярную природу. Она складывается из кинетической энергии движущихся молекул и их потенциальной энергии, определяемой взаимным притяжением и отталкиванием. Наряду с этими составляющими внутренней энергии являются энергия электронов в атомах и атомных ядер, а также лучистая энергия. Естественно, что внутренняя энергия при определенных параметрах состояния зависит от химической природы тел и их состава.
Внутренняя энергия U данного тела должна зависеть от температуры Т (кинетическая энергия молекул) и объема V (так как потенциальная энергия зависит от расстояния между молекулами). Это может быть выражено уравнением U = f(T, V), где f - функция переменных Т и V.
Возможен, однако, случай, когда при протекании процессов изменяется только кинетическая энергия, а потенциальная остается постоянной, как, например, в идеальном
15
газе. При достаточно высокой температуре и большом объеме любой газ будет вести себя как идеальный. Это означает, что потенциальная энергия взаимодействия между молекулами исчезающее мала по сравнению с их кинетической энергией и можно пренебречь собственным объемом молекул по сравнению со всем объемом, занимаемым газом. Из кинетической теории газов известно, что поведение идеального газа подчиняется уравнению Клапейрона-Менделеева:
pV = nRT,
(I.4)
где п - число молей газа в объеме V; R - универсальная газовая постоянная, равная 0,08205 л·атм/(К·моль) или 8,314 Дж/(К-моль); Т - абсолютная температура, К.
Разделив обе части уравнения (I.4) на п, получим pV = RT, где V -объем одного моля газа. Уравнение (I.4) в общем случае имеет вид f(p, V, T) = 0. Оно связывает переменные, определяющие состояние системы, и называется уравнением состояния. В термодинамике оно рассматривается как основная опытная характеристика системы. Внутренняя энергия реального газа при постоянной температуре зависит от объема, т.е. (∂U/∂V)т ≠ 0. Это обусловлено тем, что при изменении объема газа изменяются расстояния между молекулами и, следовательно, меняется потенциальная энергия. В идеальном газе внутренняя энергия не зависит от объема, так как отсутствует взаимодействие между частицами, и в этом случае (∂U/∂V)т = 0. В справедливости этого можно убедиться, рассмотрев опыт, проведенный Джоулем.
Два сосуда, соединенные краном и погруженные в воду, составляют термически изолированную систему. В сосуде I находится идеальный (разреженный) газ, а из сосуда II газ практически полностью откачан (рис. I.2). При открывании крана газ будет переходить в пустой сосуд до тех пор, пока не установится равновесное давление. При этом, как показал опыт, температура всей системы не изменяется. Если же сосуд I содержит реальный газ, то при его расширении в пустоту наблюдается изменение температуры (обычно охлаждение), так как часть запаса внутренней энергии затрачивается на преодоление сил притяжения между молекулами (опыт Джоуля-Томпсона).
Когда система участвует в тех или иных процессах, то изменяется ее внутренняя энергия. Эта энергия однозначно определяется состоянием системы, и ее изменение ΔU при любом процессе зависит только от энергии начального
16
(U1) и конечного (U2) состояний, а не от пути, по которому протекает процесс, т.е.
ΔU = U2 - U1.
(1.5)
Это является следствием закона сохранения энергии. Действительно, если при переходе системы из состояния 1 в состояние 2 изменение внутренней энергии отличалось бы по величине от соответствующего изменения при обратном переходе, то в результате такого цикла или кругового процесса возникало бы или уничтожалось некоторое количество энергии. Таким образом, внутренняя энергия имеет вполне определенное значение, для каждого равновесного состояния независимо от любых предыдущих состояний системы, т.е. она является функцией состояния. Иными словами, если охарактеризовать состояние системы, задав все ее переменные, то определится и величина U.
Это важнейшее свойство внутренней энергии, как и других функций состояния, которые будут описаны позднее, позволяет сформулировать основные соотношения термодинамики в виде связанных между собой дифференциальных уравнений.
Поскольку U является функцией состояния, то имеет смысл говорить о полном дифференциале внутренней энергии dU. Например, учитывая, что U = f(V, Т), можно написать уравнение:
dU = (∂U/∂V)тdV + (∂U/dT)VdT.
(1.6)
Для работы можно говорить лишь о ее бесконечно малом элементе, а не о полном дифференциале, так как она зависит от пути процесса и не является функцией состояния.
В изолированной системе энергетические изменения ограничиваются работой и внутренней энергией. Если система не изолирована, то она обменивается энергией с окружающей средой.
Пусть, например, цилиндр из хорошо проводящего тепло материала, наполненный идеальным газом, помещен в термостат для поддержания постоянной температуры. Если дать газу возможность расшириться, то он может произвести определенную работу. Источником этой работы является только энергия термостата, так как внутренняя энергия газа осталась неизменной: (∂U/∂V)т = 0.
Если в сосуде заключен реальный газ, то энергия термостата расходуется не только на совершение работы, но и на изменение внутренней энергии газа, так как (∂U/∂V)т ≠ 0. Таким образом, изменение внутренней энергии системы не определяется только тем, что она производит механическую работу или над ней производится такая работа. Оно может происходить и путем перехода внутренней энергии от другой
17
системы (в нашем случае от термостата). Энергия, которую система получает (или отдает) от окружающих тел, называется теплом.
Количество тепла Q, приданное системе, расходуется на увеличение ее внутренней энергии U и работу W, т.е.
Q = ΔU + W.
(I.7)
Это уравнение представляет собой аналитическую формулировку первого закона термодинамики. Для изолированной системы Q = 0 и W = 0, следовательно, ΔU = 0. Отсюда следует и другая формулировка первого закона термодинамики: внутренняя энергия изолированной системы постоянна.
При бесконечно малом процессе
δQ = dU + δW.
(1.8)
Обозначения порций тепла и работы δQ и δW подчеркивают отличие свойств этих величин от свойств внутренней энергии, так как они бесконечно малы и не являются полными дифференциалами. Внутренняя энергия характеризует состояние системы, и ее изменение не зависит от характера процессов, переводящих систему из одного состояния в другое.
В отличие от внутренней энергии понятия теплоты и работы относятся не к системе, а к процессам. Это видно хотя бы из того, что могут быть процессы, на которые не затрачивается ни работы, ни тепла, например расширение идеального газа в пустоту или процессы в изолированных системах, происходящие без теплообмена с окружающей средой. Тепло и работа проявляются только при протекании процессов, т.е. при изменениях состояния; они являются лишь формами передачи энергии, а не самой энергией. Именно поэтому не имеет смысла говорить о "запасе тепла" или о "запасе работы". Вместе с тем правильным будет, например, утверждение, что тело при данном процессе совершило определенную работу или получило определенное количество тепла.
Для термодинамического анализа явлений природы или технических процессов нет необходимости знать абсолютную величину запаса внутренней энергии тел, так как при этом имеет значение лишь изменение этой функции, которое может определяться по величинам работы и теплового эффекта, поддающимся непосредственному измерению.
18
