Эти методы заключаются, главным образом, в изучении равновесий между реальными растворами и другими фазами, в которых активность компонента известна. Такими фазами могут быть смеси идеальных газов, разбавленные или совершенные растворы, а также и другие фазы, в которых активность определена независимым путем или описывается простыми законами. Наконец, могут быть использованы и чистые вещества, активность которых равна единице. В предыдущем разделе были описаны некоторые из таких методов. Ниже приводятся примеры, характеризующие два распространенных экспериментальных метода определения активности.
Измерение давления пара. Этот способ удобен для летучих компонентов. Основанные на его использовании расчеты
144
непосредственно вытекают из уравнения (VI.2) для определения активности и достаточно просты. Однако измерение давления пара, особенно в системах, представляющих интерес для металлургии, в ряде случаев связаны со значительными трудностями (малые значения рi взаимодействие расплавов с материалами тиглей при высоких температурах).
В последние годы применение радиоактивных изотопов и масс-спектрометрии существенно облегчило получение данных о давлениях пара, в различных металлических и шлаковых растворах.
Целесообразно рассматривать отдельно определение активности в растворах, близких к совершенным и близких к разбавленным. В первом случае активность компонента i определяется из измерений давления его пара над раствором и в чистом состоянии: ai = pi/p
.
В случае металлических сплавов, где один из компонентов отличается значительной летучестью, используют метод "точки росы". Исследуемый сплав помещают в кварцевую ампулу, имеющую длинный отросток. После откачки ампулы и создания в ней высокого вакуума, отросток запаивают. Опыт состоит в том, что температуру сплава в широкой части ампулы поддерживают постоянной (Т1) и достаточно высокой, а температуру конца отростка постепенно изменяют (Т2). При некотором значении Т2 < Т1 в отростке появляются капли летучего компонента. Это и есть "точка росы", т.е. температура, при которой давление пара компонента становится насыщенным и он начинает конденсироваться на стенках кварцевого отростка. Это давление для данного вещества в чистом состоянии известно, например, из справочников. Вместе с тем оно равно парциальному давлению компонента над исследуемым сплавом в широкой части ампулы при Т.
Подобным методом было найдено, что парциальное давление пара свинца pPb при 1200° C над сплавом Cu-Pb, где xPb = 0,04, составляет 0,702·103 Па. Давление пара чистого жидкого свинца рPb в зависимости от температуры описывается уравнением:
lg p
= -(9873/
Т) - 0,66
T lg
Т + 12,066.
Отсюда следует, что при 1200° C (1473 К) р
= 2,0·10
3 Па и, следовательно,
aPb =
рPb/
р
= 0,702×10
3/2,0·10
3 = 0,356 и γ
Pb = 0,356/0,04 = 8,9.
Так как величина γPb намного больше единицы, можно
145
Таблица VI.1. Зависимость между давлением, концентрацией и активностью СО2 в воде при 0° C, гCO2 = 0,556

полагать, что в расплаве Cu-Pb имеется тенденция к расслаиванию.
В случае растворов, близких к разбавленным, активность растворенного вещества определяют с помощью уравнения p2 = r2a2. Для этого сначала находят r2. С этой целью устанавливают зависимость парциального давления р2 от концентрации вплоть до высоких разбавлений, где а2 = с2 и p2 = г2с2. Практически для разбавленных растворов экспериментально определяют отношение p2/c2 для нескольких растворов и экстраполируют его на нулевую концентрацию, где это отношение становится постоянным и равным г2.
В качестве примера в табл. VI.1 приведены результаты измерений парциальных давлений и концентраций СО2 в Н2O при 0° C, из которых найдены величины гCO2, aCO2
Из таблицы видно, что при концентрациях СО2 ниже 8,65 см3/см3 отношение pCO2/cCO2, практически постоянно, и, следовательно, равно гCO2. Видно также, что при таком разбавлении активность равна концентрации, а коэффициент активности - единице. Активность растворителя (Н2О) из приведенных данных может быть найдена с помощью уравнения Гиббса - Дюгема.
Изучение химического равновесия. Активности малолетучих веществ, например углерода, практически невозможно определять из измерений давления пара. В таких случаях целесообразно изучать химическую реакцию, в которой участвует этот компонент и образуются газообразные продукты.
Так, для раствора углерода в γ-Fe (аустенит) можно
146
воспользоваться реакцией:
[С] + 2Н2г = СН2г
(VI. 17)
константа равновесия которой
К = pCH1/p
ac
(VI.18)
Сначала выберем в качестве стандартного состояния чистый углерод в виде β-графита при аC = 1 и, следовательно, К = р
/ (
p
)
2, где индекс "ст" указывает на равновесие с графитом. В любом другом состоянии
аC < 1 и определяется из уравнения (VI.18):

Отсюда видно, что состав газовой смеси Н2-СН4 при данной температуре однозначно определяет активность углерода в растворе. Зная концентрацию углерода хC, можно найти коэффициент активности γC =
. В рассматриваемом случае наблюдаются положительные отклонения от законов совершенных растворов и γ
C > l. Действительно, из аустенита, содержащего, например, 4,63 % С (
хC = 0,184), графит выделяется при 1300° C. Поскольку при этом
аC = 1, то γ
C = 1/0,184 = 5,43.
В металлургических расчетах концентрацию часто выражают в массовых содержаниях, %, а в качестве стандартного состояния выбирают разбавленный раствор. В таком растворе активность обозначают а∞ и она равна концентрации. Например, для углерода a
= [С] при [С] → 0. При таком выборе стандартного состояния константа равновесия
Kразб для реакции (VI.17) не равна величине, определяемой уравнением (VI.18). Для определения
Кразб необходимо изучить равновесие реакции (VI.17) с участием нескольких растворов с малыми концентрациями углерода, а затем экстраполировать отношение
pCH1/
p
[С] на нулевое значение [С]. Как отмечалось ранее,
Kразб сохраняет свое значение и для более концентрированных растворов
Kразб = pCH1/p
a
=
pCH1/(
p
[C]
fC).
Зная Кразб, по составу газовой фазы можно найти аС, затем при известном значении [С] определяют fC или наоборот.
Соотношение между величинами активностей углерода,
147
найденными с использованием двух разных стандартных состояний, получается почленным делением
K/Kразб = a
/
aC = ([C]
fC)/(
xСγ
С).
Подобным же образом активность FeO в жидком шлаке любого состава может быть найдена путем изучения равновесия реакции: FeO + COг = Fe + CO2г, где К, находится по составу газовой смеси, равновесной с чистой жидкой FeO (aFeO = 1).
Я.И. Герасимовым было проведено вычисление в расплавах системы FeO-SiO2 при 1600° C, результаты которого в графическом виде представлены на рис. VI.3.
В расплавах, богатых FeO, имеются отрицательные отклонения от закона Рауля вследствие тенденции к образованию силиката Fe2SiO4.
При больших xSiO2, наблюдаются положительные отклонения, и кривая аFeO проходит через максимум.
Наличие максимума показывает, что aFeO может быть одинаковой при разных составах, т.е. возможно равновесие двух жидких фаз - расслаивание. Расслаивание вызвано тем, что жидкий кремнезем является ассоциированной жидкостью, в которой плохо растворяется FeO, не проявляющая в жидком состоянии никакой склонности к ассоциации.
Для определения активности часто используется метод измерения электродвижущих сил гальванических элементов. Его описание будет дано в гл. IX.
Результаты определений активности используются для анализа различных процессов и расчетов равновесий. Приведем некоторые примеры.
Для выяснения условий протекания реакции обезуглероживания стали при ее взаимодействии с окислительным шлаком [С]+ (FeO) = [Fe] + COг важно знать давление СО, которое определяется из уравнения: K = рCO/aCaFeO.
Величину К находят путем изучения равновесия при малых концентрациях С в металле и FeO в шлаке, когда справедливо выражение K = pCO/[С] (FeO). Затем рCO вычисляется из значений aC и aFeO, которые должны быть-
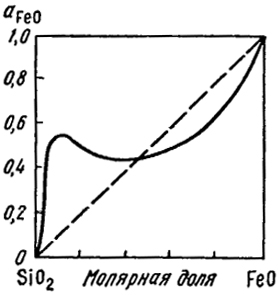
Рис. VI.3. Активность FeO в расплавах FeO-SiO
2 при 1600 "С
148
найдены из независимых опытов (например, аC из данных о химическом равновесии с газовой смесью СН4-Н2 или СО-СО2, а aFeO по растворимости кислорода в железе). Летучесть. На практике, например, при азотировании стали или синтезе ряда тугоплавких соединений, используют газы при высоких давлениях. В этих условиях вследствие взаимодействия между молекулами поведение газов отклоняется от идеального. Поэтому химический потенциал газа i отличается от величины, определяемой его фактическим давлением pi в соответствии с уравнением (V.4). В связи с этим для решения задач химического равновесия давление заменяют летучестью или фугитивностью fi, при его высоких значениях подобно тому как в реальных растворах вместо концентрации используют активность. Величина fi определяется уравнением
μi = μ
+ RT ln fi
(VI.19)
Очевидно, что при рi → 0 fi = pi. Как μi, так и fi зависят от общего давления и природы газа. Экспериментальное определение летучести основывается на уравнении (11.33). Тогда

где Vi - молярный объем чистого газа i.
При постоянной температуре dμi = Vidpi. С другой стороны, из уравнения (VI.19) dμi = RTd ln fi. Отсюда Vidpi = RTd ln fi. Вычитая из обеих частей этого уравнения RT ln pi, найдем
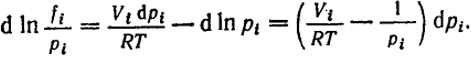
Интегрирование этого уравнения при T-const и р от 0 до pi, при котором ищут fi, приводит к выражению:
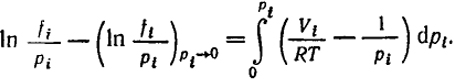 (VI.20)
(VI.20)
Второй член левой части этого уравнения равен нулю при условии fi → pi; pi → 0. Для определения величины интеграла необходимо измерить молярный объем газа Vi при различных давлениях. Величину интеграла в уравнении
149
(VI.20) можно найти графическим путем1. При малых давлениях величина [(Vi/RT) - (1/pi)] → 0, так как при этом соблюдается уравнение для идеальных газов.
Ниже приведены летучести диоксида углерода в зависимости от давления при 60° C. Видно, что летучесть меньше давления и с увеличением давления разница между fCO2, и pCO3, возрастает.

150
1
Подробное описание методов определения летучести см. в кн. Физическая химия/Под ред.
К.С. Краснова. М.: Высшая школа 1982. 687 с.
