Закон действующих масс. Пусть в реальном растворе имеет место реакция: A = 2D.
При равновесии μA = 2μD. Согласно уравнению (VI.1):
μA = μ
+ RT ln
аА = 2μ
+ 2
RT ln
aD.
Отсюда
ln(а
/
aA) = -(2μ
- μ
)/
RT =
f(
T).
Следовательно, при постоянной температуре
a
/aA = Ka.
(VI.6)
Это означает, что закон действующих масс применим для реальных растворов, если вместо концентраций используются активности.
Будет ли числовое значение константы равновесия в разбавленных и концентрированных растворах одним и тем же? Обозначим концентрации компонентов в разбавленном растворе с
и
c
. Тогда, согласно уравнению (V.16), (
c
)
2/
c. Вместе с тем при разбавлении
aA =
c
и
aD =
c
, откуда следует, что
Ka =
Kразб, т.е. константы равновесия, выраженные через активности имеют то же значение как для разбавленных, так и для концентрированных растворов.
Естественно, что если бы для последних растворов в выражении закона действующих масс использовались концентрации, то отношение c
/
cA не было бы постоянным и зависело бы от концентрации. Это вызвано тем, что вследствие межчастичного взаимодействия в различных реальных растворах концентрация отличается от активности.
Растворимость. Рассмотрим, например, связь между растворимостью кислорода в жидком железе [О] и активностью FeO в шлаке. Соответствующая
138
реакция может быть представлена уравнением [Fe] + [O] = (FeO).
Если шлак является совершенным раствором, а металл разбавленным, то
К = xFeO/[O], поскольку xFe −∼ 1.
В действительности шлак не является совершенным раствором; металл же ввиду малости концентрации в нем кислорода может рассматриваться как разбавленный раствор. Поэтому молярную долю FeO в шлаке следует заменить активностью, т.е.
K = aFeO/[O].
(VI.7)
Для того, чтобы найти К при какой-либо температуре, следует определить величины aFeO и [О]. Это можно осуществить опытным путем. Примем в качестве стандартного состояния для FeO шлак, состоящий из чистой расплавленной FeO, где aFeO = 1. Определяя концентрацию кислорода [О] в жидком железе под таким шлаком, находим величину К из уравнения (VI.7). При 1600° C указанная величина [О] = 0,23 %. Отсюда К = > 1/0,23, а при этой температуре в шлаке любого состава
аFeO = K[O] = [O]/0,23.
Таким образом, чтобы найти aFeO, следует определить концентрацию кислорода в металле, находящемся в равновесии со шлаком. Если же aFeO известна как функция состава шлака, то можно вычислить концентрацию кислорода в железе под шлаком любого состава.
В качестве другого примера рассмотрим в общем виде связь между активностью и температурой, при которой из раствора выделяются кристаллы растворителя (растворимость растворителя). Из уравнения (V.23) следует, что понижение температуры замерзания нелетучим растворенным веществом составляет ΔTз = [RT
/Δ
Hпл]
x2.
Каким путем из отклонений от этого закона можно найти активность растворителя в реальном растворе? При равновесии между кристаллами растворителя и раствором
Стандартным состоянием для растворителя является чистая жидкость, поэтому его активность в твердом состоянии определяется уравнением:
a1 = p1кр/p
.
(VI.7)
Выделение кристаллов из раствора происходит при температуре, более низкой, чем точка плавления растворителя, и, следовательно, чистая жидкость при этой температуре находится в переохлажденном состоянии и неустойчива. Давление ее пара больше давления пара над кристаллами, т.е. p
>
p1кр и
а1 < 1. Непосредственные измерения давления паров затруднительны, особенно в случае переохлажденной
139
жидкости. Для решения поставленной задачи воспользуемся уравнением Клапейрона-Клаузиуса (III.2). Логарифмируя уравнение (VI.18), -lna1 = lnp1кp - lnp
и дифференцируя результат по температуре, найдем
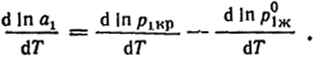
Согласно уравнению (III.2), первый член правой части равен ΔHсуб/RT2, а второй - ΔHисп/RT2, откуда
d ln a1/dT = ΔHисп/RT2.
(VI.9)
Интегрируя это уравнение, можно найти связи между активностью и температурой и активностью и концентрацией. Полагая приближенно, что ΔHпл ≠ f(T) и учитывая, что при температуре плавления чистого компонента (Тпл) соблюдаются равенства p1кр = p1ж и a1 = 1, найдем

и
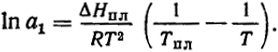 (VI. 10)
(VI. 10)
Таким образом, чтобы определить a1 нужно знать ΔHпл. Однако при этом определяемые величины активности будут относиться не только к разным концентрациям, но и к разным температурам. Поэтому, чтобы найти a1 как функцию концентрации, следует привести активности при разных концентрациях к какой-либо одной температуре, т.е. определить зависимость активности от температуры при постоянном составе раствора. Найдем такую зависимость для растворов, близких к совершенным, или для растворителя в растворах, близких к разбавленным, для которых ai = pi/p
. Логарифмируя это соотношение: ln
ai = ln
pi - ln
p
, и дифференцируя его по температуре при постоянном составе, найдем

Первый член правой части уравнения, согласно уравнению (III.2), равен парциальной теплоте испарения компонента из раствора. ΔHисп, деленной на RT2. Очевидно, ΔHиспi = ΔHi = Hпар - Hi. Теплота испарения чистой жидкости
140
ΔH
=
Hпар -
H
и соответственно второй член в правой части равен (
Hпар -
H
)/
RT2. Отсюда

H0 - Hi есть разница энтальпий компонента в чистом растворителе и в растворе данной концентрации. Эта разность с обратным знаком называется дифференциальной теплотой разбавления ΔHразб = Hi - H
и соответствует теплоте перехода моля компонента
i из состояния чистой жидкости в раствор данной концентрации. Таким образом
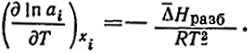
Измерения температуры кристаллизации позволяют определить активность растворителя или из данных об активности можно находить температуру кристаллизации.
Распределение компонентов между фазами. Так как закон распределения по существу является частным случаем закона действующих масс, то его формулировку можно распространить и на реальные растворы, если заменить ci на ai
Ka = aiI/aiII
(VI.12)
Для примера рассмотрим распределение фосфора между железом и серебром, которые не смешиваются в жидком состоянии:
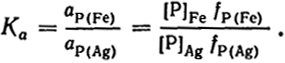
Существенным условием надежности определения активности растворенного вещества из данных о его распределении между двумя фазами является малая величина его концентрации в одной из фаз, вследствие чего ее можно рассматривать как разбавленный раствор (ci = ai). Если это не так, то необходимо определение активности компонента в этой фазе каким-либо другим способом.
Так как концентрация фосфора в серебре мала, то
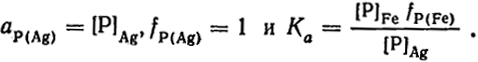
При сильном разбавлении Ka = [P]
/ [P]
. Поэтому значение константы распределения определяют из измерений
141
отношения [Р]Fe/[Р]Ag для нескольких разбавленных растворов фосфора в железе с последующей экстраполяцией на нулевую концентрацию.
Сведения о величинах fP(Fe) полезны для совершенствования технологии дефосфорации стали.
Связь между активностями компонентов. Часто удается экспериментально определить активность лишь одного из компонентов раствора. Как отмечалось выше, введение активности позволяет на основании определений одного из свойств раствора вычислить другие его свойства.
Рассмотрим способ, при помощи которого по известной активности компонента бинарного раствора находится активность другого. Согласно уравнению (V.10)
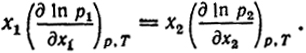
Кроме того, по определению p1 = a1p
и
p2 =
a2/
p
. Логарифмирование этих выражений ln
p1 = ln
a1 + ln
p
дифференцирование соответственно по
х1 и по
x2 при постоянных
р и
Т приводят к уравнениям
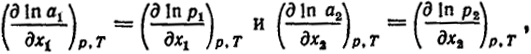
поскольку p
и
р
- постоянны.
После подстановки этих равенств в уравнение (V.10) получаем
 (VI.13)
(VI.13)
Это уравнение может быть обобщено на раствор, содержащий несколько компонентов Ϊxi(∂ ln ai/∂xi)р,T = 0. Если бинарный раствор близок к разбавленному, то для растворителя a1 = p1/p
и для растворенного вещества
a2 =
p2/г
2. Так как в бинарном растворе d
x1 = d
x2, то уравнение (VI.13) может быть представлено в более простом виде (при постоянных
р и
Т):
x1d ln a1 = -x2d ln a2.
(VI.14)
Из сказанного следует, что для определения активности одного компонента необходимо знать зависимость активности второго компонента от состава и активность первого компонента при какой-либо одной концентрации х1. Пусть, например, известна зависимость активности летучего компонента а2 от его концентрации x2. Тогда для вычисления
142
a1 следует проинтегрировать уравнение (VI.14) в пределах от концентрации х1, где известна а1, до искомой концентрации х
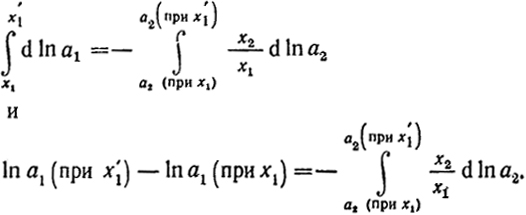
Первый компонент является растворителем и при х1 = 1 a1 = l.
Следовательно, второй член в левой части уравнения равен нулю. Таким образом,

Этот интеграл обычно определяют графически, откладывая по оси ординат отношение x2/x1, а по оси абсцисс ln a2 как это показано на рис. VI.1. Величина интеграла равна заштрихованной площади под кривой АС, лежащей правее вертикали DB, до точки, где ln a2. соответствует x1 = 1. Однако в этой области из-за малости а2 ln а2 →
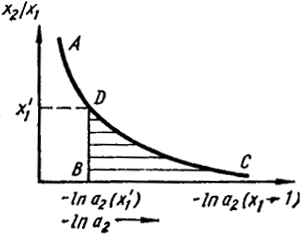
Рис. VI.1. Графическое определение активности
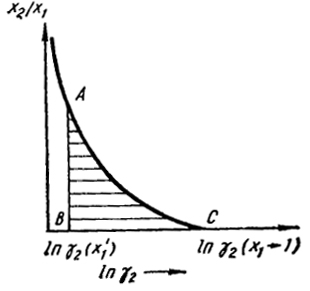
Рис. VI.2. Графическое определение коэффициента активности
143
→ ∞ и поэтому графическое интегрирование неточно. Избежать этого можно следующим простым приемом, основанным на справедливом для бинарного раствора равенстве dx1 = -dx2. Умножив и разделив обе части равенства на x1 и х2 соответственно, получим x1d ln x1 = -x2 d ln x2. После почленного вычитания этого выражения из уравнения (VI.14)
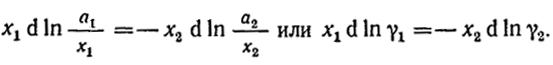
Отсюда
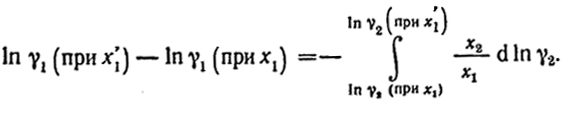 (VI.16)
(VI.16)
При x1 → 1 γ → 1. В разбавленных растворах, где х2 → 0, как уже отмечалось, химический потенциал растворенного вещества и логарифм его активности стремятся к -∞. В противоположность этому γ2 при больших разбавлениях становится постоянной величиной, не зависящей от концентрации, поскольку здесь справедлив закон Генри. Благодаря этому устраняется неопределенность графического интегрирования. В представленном на рис. VI.2 случае значение ln γ2 положительно и γ > 1. Поэтому правая сторона уравнения (VI.16) отрицательна, a ln γ1 < 0 и γ1 < l. Из этого следует, что отклонения от закона Рауля для растворителя отрицательны.
144
