§ 5. Совершенные растворы

В практике, особенно в металлургии, часто применяют концентрированные растворы, например, штейны, шлаки,

124

сплавы. Поэтому необходимо знание термодинамических свойств таких растворов. В первую очередь зависимости химического потенциала компонента от состава раствора. Для этого сначала рассмотрим идеализированный раствор, в котором компоненты очень близки по своим физико-химическим свойствам. Таковы, например, растворы изотопов или оптических изомеров. Более или менее подобны таким растворам смеси жирных углеводородов или расплавы близких по своей природе веществ (Fe-Ni, FeO-MnO). Идеализированные растворы, которые называются совершенными, характеризуются благодаря близости свойств компонентов тем, что они образуются без теплового эффекта и без изменения объема (ΔH = 0 и ΔV = 0). Вследствие этого, например в случае бинарного раствора, содержащего п\ молей первого компонента и п2 - второго, энтальпия Н и объем V выражаются уравнениями:

H = n₁H

0

1

  + n₂H

0

2

  ;
V = n₁V

0

1

  + n₂V

0

2

  . (V.26)

Из уравнения (V.26) следует, что

(∂H/≜n₁)_n2 = H

0

1

  и (∂H/≜n₂)_n1 = H

0

2

соответственно равны их энтальпиям в виде чистых веществ, например в виде чистых жидкостей.

Так как для совершенного раствора ΔH = 0, то из уравнения ΔG = ΔH - TΔS следует, что ΔG = -TΔS, т.е. тенденция к образованию такого раствора определяется только увеличением энтропии. Отсюда также следует, что в отличие от величин H и V энергия Гиббса и энтропия при образовании совершенного раствора неаддитйвны. Очевидно, энтропия раствора определится уравнением:

S = n₁s

0

1

  + n₂s

0

2

  + ΔS, (V.27)

где ΔS - энтропия смешения.

Изменение энтропии при образовании раствора может быть вычислено по уравнению: ΔS = k ln(ω/ω₀). Величины ω и ω₀ представляют собой термодинамические вероятности раствора и компонентов до смешения. Пусть бинарный раствор содержит М₁ молекул первого компонента и М₂ второго. При смешении объем системы не изменится но вероятность состояния возрастет вследствие того, что молекулы разных компонентов могут обмениваться местами. Это возрастание определяется числом перестановок

125

молекул между собой (П), которые делаются возможными вследствие образования раствора: ω = ω₀П.

Если бы все молекулы были разными, то число перестановок составило бы (M₁ + M₂)!. Но так как имеется М₁, и М₂ одинаковых молекул, перестановки которых друг на место друга не дают нового состояния, то следует величину (M₁/M₂)! поделить на M₁! и М₂! так, что ω = ω₀ = [(M₁ + M₂)]/(M₁M₂) или

ΔS = k ln [(M₁ + M₂)!]/(M₁!M₂!). (V.28)

Для нахождения ΔS используем приближенную формулу Стерлинга: ln В! = В 1п В-В, которая становится точной при очень больших В.

Таким образом:

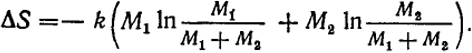
Учитывая, что M₁ = n₁N_A и M₂ = n₂N_A, где N_A - число Авогадро, и что R = kN_A, найдем:

(V.29)

Разделив обе части уравнения на (п₁ + п₂), получим изменение энтропии при образовании одного моля совершенного раствора:

ΔS = -R(х₁ ln x₁ + x₂ ln х₂),

где х₁ и х₂ - молярные доли компонентов.

Так как в бинарном растворе x₁ = l - x₂, то опуская индексы это уравнение можно представить в виде:

ΔS = -R[x₁ ln x + (1 - х) ln (1 - х)]. (V.30)

Отсюда, учитывая, что для совершенного раствора ΔG = -TΔS:

ΔG = RT[x ln x + (1 - x) ln (1 - x)].

Так как величины х всегда меньше единицы, то ΔG всегда отрицательно, т.е. совершенный раствор образуется самопроизвольно при любых концентрациях. Из приведенного вывода следует, что уравнение (V.30) справедливо и для случая смешения двух идеальных газов. Иногда полагают, что образование растворов возможно лишь благодаря химическому взаимодействию между компонентами. Этому утверждению противоречат факты смешения идеальных газов во всех отношениях, а также образования растворов, близких к совершенным без изменения внутренней энергии

126

(энтальпии). Химическое взаимодействие в конденсированных фазах может ослабить или усилить тенденцию к образованию растворов, обусловленную увеличением вероятности и изменением ΔH_см.

Подставляя уравнение (V.29) в (V.27) и дифференцируя по п₁ при постоянном п₂, найдем парциальную молярную энтропию первого компонента, т.е.

S₁ = S

0

1

  - R ln x₁,

а дифференцируя по n₂ при постоянном п₁, найдем

S₂ = S

0

2

  - R ln x₂.

Так как G_i = H_i - TS_i, то, используя найденные выражения для H₁, H₂, S₁ и S₂, получим выражение для G₁ = μ₁, т.е.

μ₁ = H

0

1

  - TS

0

1

  + RT ln x₁,

Величина H

0

1

  - TS

0

1

  = μ

0

1

  представляет собой молярную энергию Гиббса чистого первого компонента, например чистой жидкости, и, следовательно,

μ₁ = μ

0

1

  + RT ln x₁. (V.31)

На основании таких же соображений

μ₂ = μ

0

2

  + RT ln x₂. (V.32)

Эти соотношения, совпадающие с уравнением (V.19) для химического потенциала растворителя в разбавленном растворе, показывают что в совершенном растворе для любого компонента i химический потенциал выражается уравнением:

μ_i = μ

0

i

  + RT ln x_i (V.33)

Рассмотрим равновесие между бинарным совершенным раствором и его паром, подчиняющимся законам идеальных газов. Из уравнения (II.8) следует, что G₁ = G

0

1

  + RT ln p₁ и G₂ = G

0

2

  + RT ln p₂.

Так как G₁ = μ, то с учетом уравнения (V.31)

G

0

1

  + RT ln p₁ = μ

0

1

  + RT ln x₁, или ln (x₁/p₁ = (G

0

1

  - μ

0

1

  )/RT.

Следовательно, при постоянной температуре отношение x₁/p₁ = K₁ тоже постоянная величина. Приравнивая G₂ и μ₂, точно так же найдем, что х₂/р₂ = К₂. В отличие от разбавленных растворов уравнения (V.31) и (V.32) справедливы при любых значениях x₁ и х₂ от 0 до 1. Таким образом,

127

принимая x₁ = l, находим, что K₁ = l/p

0

1

  , и, принимая x₂ = 1, -К₂ = 1/р

0

2

  , где р

0

1

  и р

0

2

  - давления пара чистых жидкостей.

Отсюда следует, что для обоих компонентов бинарного совершенного раствора при любых концентрациях справедлив закон Рауля: р₁ = р

0

1

  /x₁ и р₂ = p₂ = p

0

2

  /x₂ю

Таким образом, в отличие от разбавленных растворов, где растворитель и растворенное вещество подчиняются различным законам, в совершенных растворах все компоненты при любых концентрациях подчиняются одному и тому же закону, а именно закону Рауля. Это позволяет определить совершенный раствор как раствор, все компоненты которого подчиняются закону Рауля в широком интервале температур и давлений.

Законы разбавленных растворов верны для любых веществ, однако лишь при большом разбавлении. Законы совершенных растворов справедливы лишь для некоторых веществ, но при любых концентрациях. Заметим, что разбавленные растворы можно рассматривать как совершенные в отношении растворителя. Действительно, смешение растворителя с таким раствором происходит без теплового эффекта; выражения для химического потенциала и давления пара растворителя совпадают с соответствующими выражениями для компонентов совершенных растворов.

Полученные выше соотношения позволяют рассмотреть некоторые конкретные равновесия для совершенных растворов подобно тому, как это было сделано для разбавленных растворов.

Давление пара. Закон Рауля позволяет выразить связь между давлением пара совершенного бинарного раствора и его составом в виде простого уравнения. Поскольку общее давление пара над раствором р₀ равно сумме давлений паров компонентов р₁ и р₂, то p₀ = p

0

1

  x₁ + p

0

2

  x₂ или, учитывая, что x₁ = 1 - x₂, p₀ = p

0

1

  + (p

0

2

  - p

0

1

  )x₂.

Следовательно, при постоянной температуре давление пара над таким раствором является линейной функцией его состава. Из закона Рауля следует, что парциальные давления компонентов также линейно зависят от состава. Это иллюстрируется рис. V.7, на котором представлена диаграмма давление пара - состав для бинарного совершенного раствора.

Закон действующих масс. Пусть в гомогенном совершенном растворе протекает реакция: A_{раствор} = 2B_{раствор}.

При равновесии μ_A = 2μ_B или μ

0

A

  + RT ln x_A = 2μ

0

B

  +

128

+ 2RT ln x_B. После преобразования найдем, что ln x

2

B

  /x_A = f(T) или x

2

B

  /x_A = К.

Таким образом, для реакций между компонентами совершенных растворов справедлив закон действующих масс. При этом концентрации реагирующих веществ должны быть выражены в молярных долях. Напомним, что в случае разбавленных растворов закон действующих масс справедлив при любом способе выражения концентрации.

Так как μ

0

i

  = G⁰, то для рассмотренной выше реакции ΔG⁰ = 2G

0

B

  - G

0

A

  = -RT ln K.

Отсюда следует, что константа равновесия для реакции, протекающей в совершенном растворе, может быть вычислена из данных о энергиях Гиббса чистых компонентов.

Ряд важных металлургических реакций протекает при взаимодействии двух растворов - металлического и шлакового. Если эти растворы близки по свойствам к совершенным, то целесообразно выражать концентрации в обеих фазах в молярных долях. Это относится, например, к реакции распределения марганца между железом и расплавом FeO-МnО:

[Mn] + (FeO) = (MnO) + [Fe],

где равновесие определяется условием:

μ

0

[Mn]

  + RT ln x_Mn + μ

0

(FeO)

  + RT ln x_(FeO) = μ

0

(MnO)

  + RT ln x_(MnO) + μ

0

[Fe]

  + RT ln x_[Fe].

Отсюда следует, что K = x_(MnO)/x_[Mn]x_(FeO), так как x_[Fe] −∼ 1.

В ряде случаев в реакции принимает участие компонент шлака, находящийся в нем в большой концентрации, в то время как его содержание в металле очень мало. Примером может служить раскисление железа марганцем с образованием расплава FeO-MnO: [0] + [Mn] = (MnO).

Здесь металлический раствор можно считать разбавленным относительно кислорода, а шлаковый - совершенным относительно MnO и, следовательно, при равновесии

129

Очевидно, для вычисления K в подобных случаях, кроме табличных данных о термодинамических функциях чистых компонентов, необходимы данные и для компонентов в растворенном состоянии при одной (стандартной) концентрации.

Для того, чтобы рассчитать выход реакции между совершенными растворами, например, потерю марганца при взаимодействии железа с окислительным шлаком, следует из таблиц стандартных величин найти величину ΔG

0

298

  для реакции между чистыми веществами и определить К для температуры 298 К из соотношения ΔG

0

298

  = -19,14×298 ln К.

Затем следует вычислить величину K для интересующей нас высокой температуры, пользуясь известным уравнением d ln K/dT = ΔH/RT², учитывая, что в величину Δ должны войти теплоты фазовых и агрегатных превращений.

Растворимость. Процесс растворения твердого тела в жидкости можно представить уравнением: A_т = A_p.

Если образующийся раствор совершенный, то, согласно закону действующих масс, в этом случае x_A = К, следовательно, каждой температуре соответствует определенная растворимость, т.е.

d ln x_A/dT = ΔH/RT²,

где ΔH - изменение энтальпии при растворении.

Величина ΔH представляет собой сумму теплот плавления ΔH_пл = ρ и смешения образовавшейся жидкости с раствором ΔH_см. В случае совершенного раствора теплота смешения равна нулю, и, таким, образом, теплота растворения равна теплоте плавления и d ln x_A/dT = ρ/RT².

Это уравнение справедливо для выделения А(T) при всех концентрациях и температурах вплоть до x_A = 1. Интегрирование приведенного уравнения в пределах от некоторой температуры Т до Т_пл (Т < Т_пл) приводит к выражению для так называемой идеальной растворимости:

где x

’

A

  относится к Т, а x_A - к T_пл.

Таким образом, чем выше Т_пл и ρ данного вещества, тем

130

меньше его растворимость. Зная энтальпию плавления вещества и температуру его плавления, можно оценить идеальную растворимость. Например, энтальпия плавления меди составляет 12970 Дж/моль, а температура плавления 1083° C (1356 К). Отсюда, например, при 880° C (1253 К)

lg x_Cu =

12970

19,14

  (

1

1356

  -

1

1253

) = -0,0418

и x_Cu = 0,91.

Экспериментальная величина х_Cu при этой температуре в сплаве Cu-Pb равна 0,92. Подобный расчет для сплава Cu-La при 1000° C дает x_Cu = 0,93 вместо экспериментального значения 0,96. Следует, однако, иметь в виду, что вообще применение законов разбавленных и совершенных растворов к реальным металлургическим системам сопряжено с трудностями.

131