Цель термодинамической теории растворов состоит в том, чтобы связать различные свойства растворов и найти способы предсказания свойств растворов, исходя из свойств чистых, компонентов. Ввиду очень сложного характера взаимодействия компонентов в растворах решение этой задачи в общем виде невозможно. Поэтому целесообразно сначала рассмотреть идеализированные случаи, в которых можно
105
отделить главные черты явления от второстепенных. В связи с этим в теории растворов рассматриваются два основных типа идеальных растворов: бесконечно разбавленные (или просто - разбавленные) растворы и совершенные растворы.
Если обозначить индексом 1 растворитель, а индексом i (i = 2, 3, 4 ...) растворенное вещество, то разбавленный раствор можно определить как такой, в котором х1 → 1, а xi → 0. Особенностью такого раствора является то, что молекулы растворённого вещества отделены друг от друга большим числом молекул растворителя. Поэтому имеет место только взаимодействие между растворенным веществом и растворителем, но не между молекулами растворенного вещества. Вследствие этого, если к разбавленному раствору при постоянной температуре добавлять растворитель, то при разбавлении раствора с увеличением его объема не будет изменяться ни энергия U, ни энтальпия Н системы раствор - растворитель:
(∂U/∂V)T = ∂(H/∂V)T = 0,
подобно тому, как это имеет место в смесях идеальных газов.
Вообще между веществами в состоянии бесконечно разбавленного раствора и в состоянии идеального газа существует аналогия, на которую впервые указал Вант-Гофф. Растворенное вещество имеет тенденцию самопроизвольно распространяться в объеме растворителя подобно тому, как газ расширяется в пустоту. Поэтому возможно сопоставление термодинамических свойств идеального газа и разбавленных растворов.
Свойства всякого вещества, в том числе и его уравнение состояния, с точки зрения термодинамики определяются внутренней энергией и энтропией этого вещества. Рассмотрим в качестве примера идеальный газ и покажем, что его уравнение состояния может быть найдено из выражений для его энергии и энтальпии. Как ранее указывалось, отсутствие потенциальной энергии у идеального газа приводит к выражению:
(∂U/∂V)T = 0.
(V.14)
Если в соответствии с изложенным в гл. II материалом принять, что вероятность пребывания одной молекулы в данном объеме пропорциональна величине этого объема, то для одного моля ω = k'VNA, где k' - коэффициент пропорциональности
106
и NA - число Авогадро. Отсюда
S = k’’ ln ω = k’’ NA ln V + k’’ ln k1.
(V.15)
В качестве коэффициента пропорциональности в выражении (V.15) не используется постоянная Больцмана k, так как эта величина была введена при использовании уравнения Клапейрона, которое мы собираемся сейчас вывести.
Построим выражение для энергии Гельмгольца одного моля идеального газа. Поскольку A = U - TS и U не зависит от V, то A = f(T) - Tk’’ NA ln V, где f (Т) = V - Tk’’ ln k’.
Поскольку (∂А/∂V)T = -р, то p = k’’NAT/V. Последнее выражение представляет собой уравнение Клапейрона, если k равно постоянной Больцмана, т.е. pV = RT.
Тенденция идеального газа к расширению, мерой которого является давление, описываемое уравнением Клапейрона, поэтому определяется только увеличением энтропии при расширении, так как внутренняя энергия газа при этом остается постоянной. Подобно этому тенденция растворенного вещества распространяться в объеме раствора также обуславливается лишь увеличением энтропии, поскольку в разбавленном растворе молекулы растворенного вещества не взаимодействуют друг с другом и их внутренняя энергия при разбавлении не изменяется.
Процесс разбавления разбавленного раствора аналогичен процессу расширения идеального газа. Эта аналогия заключается в том, что в обоих случаях внутренняя энергия остается постоянной, а вероятность пребывания молекулы в данном объеме пропорциональна объему, поэтому для энтропии справедливо уравнение (V.15). Такая аналогия между идеальным газом и разбавленным раствором позволяет найти выражение для химического потенциала растворенного вещества. При добавлении молекул растворенного вещества в разбавленный раствор, как уже отмечалось выше, происходит взаимодействие только между молекулами растворенного вещества и растворителя. Отсюда следует, что добавление каждой новой молекулы растворенного вещества в раствор сопровождается таким же приращением внутренней энергии (или энтальпии), как при введении ее в чистый растворитель. Иными словами, парциальная молярная энтальпия растворенного вещества (∂Н/∂n2)р.T.nj(i ≠ = H2 в разбавленном растворе является постоянной величиной, которую обозначают H2.
Для расчетов различных равновесий в разбавленных
107
растворах необходимо знать парциальную энергию Гиббса (химический потенциал) растворенного вещества G2 = H2 - TS2.
Мы доказали, что парциальная энтальпия не зависит от состава, т.е. H2 = H2. Таким образом, задача сводится к определению S2.
На какую величину изменяется энтропия разбавленного раствора при добавлении одной молекулы растворенного вещества? Это изменение обусловлено двумя факторами. Во-первых, это "энтропия положения". Определенной величиной энтропии такого вида обладают, например, молекулы в чистых конденсированных веществах. Энтропия положения обусловлена характеристиками движения (частота колебания и т.п.) и в разбавленном растворе не зависит от концентрации из-за отсутствия взаимодействия между молекулами растворенного вещества. Во-вторых, кроме энтропии положения, молекула растворенного вещества будет иметь энтропию, связанную с возможностью ее перемещения в объеме раствора.
В соответствии с описанной выше аналогией между разбавленным раствором и идеальным газом рассматриваемый вклад в энтропию для одного моля газа описывается выражением R ln V [см. уравнение (II.25)]. Если вместо V1 ввести c2 = 1/V, получим для этого вклада величину - R ln c2. Таким образом, парциальная энтропия S2 = S2 - R ln c2. Здесь в член S2 входят величины, не зависящие от с2. Отсюда следует, что
μ2 = G2 = H2 - TS2 = H2 - TS2 + RT ln c2 = ψ
+ RT ln c2,
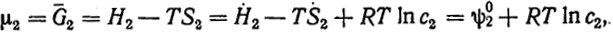 \
\
где ψ
=
H2 -
TS2 - величина, зависящая от температуры,
имеющая смысл химического потенциала растворенного вещества при концентрации, равной единице, при условии, что раствор сохраняет свойства разбавленного.
Давление пара растворенного вещества. Наиболее важным фактором, определяющим растворимость газов в жидкостях, является их парциальное давление. Согласно закону, найденному Генри опытным путем, при постоянной температуре количество растворенного газа в данном объеме растворителя пропорционально парциальному давлению газа.
108
Пусть идеальный газ при постоянной температуре находится в соприкосновении с жидкостью, в которой он может растворяться. Условие равновесия распределения растворенного вещества между газом и жидкостью заключается в равенстве его химических потенциалов в этих фазах, т.е. μ2газ = μ2раствор или, согласно уравнениям (II.33) и (V.16):
μ
+
RT ln
p2 = ψ
+
RT ln
c2.
Отсюда
p2/c2 = (ψ
- μ
)/
RT.
Так как величины ψ
и μ
зависят только от температуры, то отношение
с2/
р2, являясь функцией температуры, при ее постоянстве также постоянно. Отношение
с2/
р2 обозначается буквой г, носящей название постоянной Генри. Таким образом, закон Генри имеет вид:
p2/c2 = г2 и p2 = гс2.
(V.17)
Это уравнение позволяет рассматривать закон Генри как описание зависимости парциального давления растворенного вещества над разбавленным раствором от его концентрации.
Так как в разбавленном растворе все выражения для концентрации пропорциональны друг другу, то закон Генри справедлив при любом способе выражения концентрации. Закон Генри может быть выведен и из простых кинетических рассуждений.
Скорость перехода газа в раствор и ω↓ пропорциональна его парциальному давлению, т.е. ω↓ = k1p2, а скорость его испарения ω↑ пропорциональна концентрации: ω↓ = k2c2. При равновесии ω↓ = ω↑ и, следовательно, p2c2 = k2/k1 = г2.
Важно, что уравнение (V.17) справедливо, если вещество не меняет своей молекулярной массы при растворении. Например, при растворении азота в воде, в которой он существует в виде двухатомных молекул, процесс растворения выражается уравнением:
N2газ = N2 в водном растворе и pN2 = гN2cN2.
В металлах многоатомные газы, в том числе и азот, не растворяются в молекулярном состоянии, а находятся в растворе в виде атомов. Это объясняется тем, что при растворении необходимо раздвинуть частицы металла, сильно взаимодействующие друг с другом. При растворении молекул с насыщенными внутренними связями между
109
атомами эта затрата энергии не компенсируется увеличением энергии вследствие взаимодействия между металлом и растворенным веществом. Такая компенсация, однако, в некоторой степени имеет место при растворении, если вещество, находящееся в виде молекул диссоциирует на атомы.
Растворение, например, азота в твердом или жидком железе сопровождается диссоциацией его молекул:
N2газ = 2Nраствор в Fe.
В этом случае условие равновесия имеет вид:
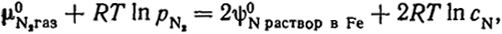
откуда

Вообще растворимость двухатомных газов (N2, O2, Н2 и т.п.) в металлах пропорциональна не их парциальному давлению, а корню квадратному из этой величины. Этот факт известен как закон Сивертса.
Растворение какого-либо газа А в конденсированной фазе можно рассматривать как реакцию: Aгаз = Aраствор, константа равновесия которой Kp = cA/pA является величиной, обратной константе Генри Kp = 1/гA. Величина 1/гA также называется коэффициентом растворимости, так как она численно равна растворимости при давлении 1 атм.
Константа Генри описывает равновесие газ - раствор, поэтому должна зависеть от температуры по тому же закону, что и константа равновесия для химических реакций:
где ΔHA - изменение энтальпии при растворении.
Растворение газов в обычных жидкостях сопровождается выделением тепла, которое по природе аналогично теплоте конденсации и ΔHA < 0. Таким образом, в этом случае 1/гA увеличивается с температурой и, следовательно, при данном давлении растворимость падает.
При растворении газов в металлах обычно тепло затрачивается, во-первых, на диссоциацию молекул и, во-вторых, на раздвижение атомов металла, что не компенсируется
110
энергией растворения. Вследствие этого растворимость газов в металлах, как правило, увеличивается с повышением температуры.
Интересно отметить, что растворимость азота в α-Fe увеличивается с повышением температуры, а в γ-Fe, наоборот, уменьшается. В некоторых случаях энергия взаимодействия атомов газа и металла столь велика, что превышает затраты энергии на диссоциацию и раздвижение атомов металла. Поэтому при растворении газа в металле происходит выделение тепла, а растворимость уменьшается с ростом температуры. Это имеет место, например, при растворении водорода в титане.
Как уже отмечалось, для разбавленных растворов все выражения концентрации пропорциональны друг другу. Поэтому закон Генри справедлив при любом способе выражения концентрации. Растворимости азота и водорода массовое содержание, % в жидком железе при 1600° C определяются уравнениями:

где парциальные давления выражены в атм.
Для практики существенно, что растворимость этих газов в жидком железе значительно выше, чем в твердом, поэтому при кристаллизации жидкой стали могут возникать дефекты из-за присутствия газовых пузырей. Растворимость газов в металлах заметно зависит от концентрации других элементов. Так, присутствие углерода уменьшает растворимость азота в жидком железе, а ванадий значительно увеличивает ее. Влияние третьего компонента на растворимость газов впервые было установлено И.М. Сеченовым, изучавшим поглощение углекислого газа кровью. Им было найдено уравнение:
lg(c2,0/c2) = ссоль,
где с2,0 и с2 - растворимости газа в чистой воде и в растворе соли; cсоль - концентрация соли.
Явление высаливания объясняется тем, что вблизи ионов свойства растворителя изменяются и, в частности, уменьшается его способность растворять другие вещества.
Давление пара растворителя. Уравнение Гиббса-Дюгема позволяет найти давление пара растворителя р1 в зависимости от его концентрации, если известна зависимость давления пара растворенного вещества тоже как функция концентрации.
Выражая концентрацию в молярных долях и логарифмируя
111
выражение (V.17), получим уравнение:
ln x2 - ln p2 - ln г2,
дифференцирование которого по х2 дает:
d ln р2/dx2 = 1/х2 или х2 (d ln p2/dx2) = 1.
Отсюда, согласно уравнению (V.10)
x1
= 1 и ln
p1 = ln
x1 + ln
C,
где С - константа интегрирования и p1 = Cx1. Для определения С примем x1 = 1, тогда, очевидно, р1 равно давлению пара чистого растворителя, т.е. р
:
p1 = p
x1.
(V.18)
Это уравнение выражает закон Рауля, согласно которому давление пара растворителя над раствором меньше, чем давление пара чистого растворителя, и пропорционально молярной доле растворителя.
Исторически этот закон был открыт эмпирическим путем на основании измерений давления пара различных органических растворителей над растворами. Рауль предложи для него следующую формулировку, равносильную уравнению (V.18): относительное понижение давления пара растворителя равно молярной доле растворенного вещества или
(p
-
p1)/
p
=
n2/(
n1 +
n2) =
x2.
В отличие от закона Генри, где коэффициент пропорциональности г не имеет простого смысла, в уравнении (V.18) этот коэффициент равен величине давления пара растворителя p
. Кроме того, закон Генри справедлив при любом способе выражения концентрации, а закон Рауля требует, чтобы она выражалась в молярных долях. Оба закона справедливы для разбавленных растворов. Так как давление пара чистого растворителя больше, чем его давление над раствором, то раствор и чистый растворитель не могут быть в равновесии.
Поместив в замкнутое пространство (например, под колпак) два открытых сосуда, один из которых с чистым растворителем, а другой с раствором, можно наблюдать самопроизвольный процесс перегонки растворителя в раствор. Это означает, что химический потенциал растворителя в любом растворе меньше его молярной энергии Гиббса в чистом состоянии, и процесс образования раствора происходит
112
с уменьшением энергии Гиббса. Из этого следует, что наличие растворенного вещества уменьшает тенденцию растворителя к испарению.
Основываясь на законе Рауля, можно найти выражение для химического потенциала растворителя в разбавленном растворе. При равновесии между растворителем в растворе и его паром над раствором химический потенциал растворителя равен молярной энергии Гиббса пара. Если пар подчиняется законам идеальных газов, то
G1 = G
(
T) +
RT ln
p1 = μ
1.
Согласно уравнению (V.18) p1 = p
x1. Подставляя это значение в выражение для μ
1, получим:
μ1 = G
(T) + RT ln p
+ RT ln x1, или μ1 = μ
+ RT ln x1,
(V.19)
где μ
- химический потенциал чистого растворителя, равный
G
+
RT ln
p
.
Температуры кипения и замерзания разбавленных растворов нелетучих веществ. Из закона Рауля вытекают важные следствия, касающиеся температур кипения и замерзания растворов. Первым из таких следствий является понижение давления пара растворителя, которое приводит к повышению температуры кипения растворов. Кипение жидкости наступает при температуре, при которой давление ее насыщенного пара становится равным внешнему атмосферному рвн. Над разбавленными растворами нелетучих веществ давление насыщенного пара равно давлению пара растворителя р1. Так как последнее всегда меньше, чем р
, то кипение будет достигаться при более высокой температуре, чем в случае чистого растворителя. Это схематично показано на рис. V.3, где
T1 и
Т0 - соответственно температуры кипения раствора и растворителя и
T1 -
Т0 = Δ
Tк - повышение температуры кипения. При температуре кипения
p 1 =
p
x1 =
pвн. Логарифмируя это уравнение и дифференцируя по температуре, получим:
d ln x1/dT = -d ln p
/d
T.
Так как по уравнению Клапейрона-Клаузиуса d ln p/dT = -ΔHисп/RT2, то dlnx1/dT = -ΔHисп/RT2 где ΔHисп - молярная теплота испарения растворителя из раствора.
113
Интегрирование в интервале между Т0 и T1 дает:
ln
=
= -
.
(V.20)
В разбавленных растворах x2 ≪ x1. Поэтому при разложении вряд выражения ln x1 = ln(1 - х2) = -x2 - x
/2 -
x
/3 можно ограничиться первым членом с точностью до 1 %, если
x2 ≪ 0,02.
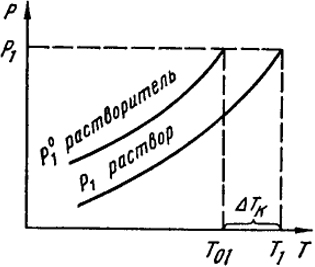
Рис. V.3. Повышение температуры кипения раствора
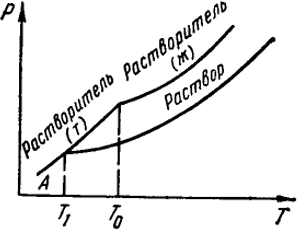
Рис. V.4. Понижение температуры замерзания раствора
В случае разбавленных растворов Т1 и Т0 различаются незначительно и произведение Т1Т0 может быть заменено Т
величина Δ
Hисп не отличается заметно от теплоты испарения чистого растворителя. Таким образом, из уравнения (V.20) следует, что Δ
Tк =
RT
/Δ
Hиспx2.
Выразим концентрацию раствора через моляльность т, Пусть раствор содержит n2 молей растворенного вещества в 1000 г растворителя. В этом случае n2 = m. Если молярная масса растворителя М1, то х2 =
. В разбавленном растворе можно пренебречь величиной
т по сравнению с 1000/
М1, тогда
х2 =
mM1/1000. Отсюда

где l = ΔHисп/M1 - удельная теплота испарения растворителя; Kэ = RT
/1000
l - постоянная величина - эбулиоскопическая
114
константа, которая характеризует свойства растворителя.
Из уравнения (V.21) следует, что повышение температуры кипения разбавленного раствора не зависит от природы растворенного вещества, а определяется только природой растворителя и моляльностью. Таким образом, величина Kэ характеризует повышение температуры кипения раствора, содержащего 1 моль любого вещества в 1000 г растворителя. В действительности Kэ может и не быть равной повышению температуры кипения моляльного раствора, так как при такой концентрации не обязательно сохранятся свойства разбавленного раствора. Поэтому Kэ обычно определяют экстраполяцией на нулевую концентрацию отношения ΔTк/m. Уравнение (V.21) было подтверждено многочисленными опытными данными для водных растворов и растворов органических жидкостей. Впоследствии будет показано, что оно неприменимо в такой простой форме к растворам электролитов.
В качестве примера вычислим величину Кэ для воды; T0 = 373 К, а l = 2255,2 Дж/г:
Kэ =
= 0,512
0.
Отсюда можно найти, например, температуру кипения раствора, содержащего 1 г сахара (М = 342) в 1000 г воды:
ΔTк = 0,512
= 0,0015° C и
Tк = 100,0015° C.
Из уравнения (V.21) следует, что измерения температур кипения растворов могут служить для определения молекулярной массы растворенного вещества. Если масса растворителя g1, а растворенного вещества с массой M2 - g2, то моляльность

Другим весьма важным следствием понижения давления пара раствора нелетучим растворенным веществом является то, что температура замерзания раствора становится ниже температуры замерзания чистого растворителя, которая определяется условием равенства давления его пара над жидкой и твердой фазами. Если при замерзании раствора выделяется чистый растворитель, то давление пара над раствором также должно быть равно давлению растворителя в твердом состоянии. Как видно из рис. V.4, это приводит к понижению температуры замерзания раствора.
Согласно уравнению Клапейрона-Клаузиуса для растворителя
115
в твердом и жидком состоянии

Предполагая, что второе уравнение справедливо для переохлажденной жидкости, и вычитая его из первого, найдем
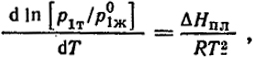
где ΔHпл = ΔHсуб - ΔHисп - теплота плавления (согласно закону Гесса).
При температуре замерзания раствора p1т = p1 (точка А), и, следовательно, d ln [p1/p
]/dT = Δ
Hпл/
RT2 или, учитывая уравнение (V.18), имеем:
d ln x1/dT = ΔHпл/RT2
(V.22)
Это уравнение, выведенное Ф.Н. Шредером, дает зависимость температуры замерзания разбавленного раствора от состава, а также выражает изменение растворимости растворителя при изменении температуры. Используя такие же соображения, как при выводе уравнения (V.21), легко получить из уравнения (V.22) выражение для понижения температуры замерзания:
 (V.23)
(V.23)
где Kз - криоскопическая постоянная, т.е. понижение температуры замерзания моляльного раствора, определяемое уравнением: Kз = RT
/1000
q, где
q - удельная теплота плавления растворителя;
Т0 - его температура плавления (замерзания).
Величина Kз зависит только от свойства растворителя. Поэтому понижение температуры замерзания разбавленных растворов в данном растворителе определяется только концентрацией растворенного вещества.
Применение уравнения (V.23) может быть показано на примере железа, теплота плавления которого составляет 262,5 Дж/г, а температура плавления Т0 = 1813 К и Кз = 8,314·18132/1000·262,5 = 101,5 К.
Таким образом, если из расплава кристаллизуется чистое железо, то понижение температуры плавления в расчете на один моль растворенного вещества в 1000 г железа должно составлять 101,5° C. Это наблюдается с известным
116
приближением для растворов серы и бора (MS = 32 и Мв = 10,82).
В первом случае экспериментально найденное понижение температуры плавления 1%-ного по массе раствора составляет 30° C. Моляльность такого раствора m = 10/32 −∼ 0,31 и ΔT3 = 101,5·0,31 = 32 К.
Во втором случае 1 % В понижает температуру плавления железа на 90 К, моляльность т = 10/10,82 = 0,92 и ΔTз = 101,5·0,92 = 93,4 К.
Подобно уравнению (V.21) уравнение (V.23) может быть использовано для определения молекулярной массы растворенного вещества.
Если кристаллизующийся растворитель содержит некоторое количество растворенного вещества, то вместо (V.23) справедливо уравнение: ΔTз = Kзm(L - 1), где L = х2т/х2ж - отношение молярных долей растворенного вещества в твердой и жидкой фазах.
Явление понижения температуры плавления растворов имеет важное значение как в природе, так и в технике. Например, выплавка чугуна из железной руды существенно облегчается тем, что температура плавления восстановленного железа понижается примерно на 400° C благодаря тому, что в нем растворяется углерод и другие элементы. То же относится и к тугоплавким оксидам, составляющим пустую породу, которые вместе с флюсами (СаО) образуют раствор (шлак), плавящийся при относительно низкой температуре. Это позволяет осуществлять непрерывно периодический процесс в доменных печах, выпуская из них жидкие чугун и шлак.
Осмотическое давление. Впервые явление осмоса наблюдал Нолле, помещая раствор сахара в стеклянную трубку, закрытую снизу полупроницаемой перепонкой и погружая ее в чистую воду. При этом вода проникала через перепонку и уровень раствора в трубке повышался, как это показано на рис. V.5.
Давление, которое необходимо приложить к раствору и достаточное для того, чтобы растворитель не проникал в раствор, называется осмотическим. Выражение "осмотическое давление" неточно, так как в растворе его не существует и оно проявляется только в том случае, если раствор отделяется от растворителя полупроницаемой перегородкой (проницаемой для молекул растворителя и не пропускающей растворенное вещество).
Вместе с тем осмотическое давление подобно газовому в том смысле, что оно является следствием стремления молекул
117
растворенного вещества занимать весь объем растворителя. Однако вследствие непроницаемости перегородки для молекул растворенного вещества в раствор проникают лишь молекулы растворителя.
Представим себе цилиндр, в нижней части которого находится раствор, отделенный полупроницаемой перегородкой от чистого растворителя. Если перегородка не закреплена, то проникновение растворителя в раствор вызвало
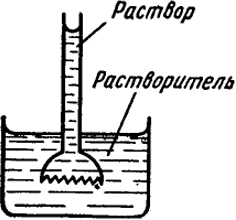
Рис. V.5. К понятию об осмотическом давлении раствора
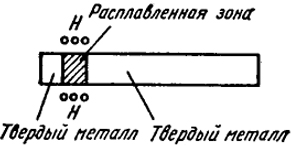
Рис. V.6. Схема зонной плавки
бы ее перемещение вверх. Осмотическое давление П, заставляющее перегородку оставаться на месте, является, таким образом, тем давлением, которое следует, приложить к раствору, чтобы он находился в равновесии с растворителем. Это равносильно тому, что оно увеличивает давление пара растворителя над раствором р1 до величины его давления в чистом состоянии р
. Поэтому П можно рассматривать и как внешнее давление, увеличивающее давление пара над раствором.
Чтобы найти связь между этими величинами, следует рассмотреть равновесие между жидкостью и ее паром. При постоянной температуре энергии Гиббса жидкости и пара равны. Используя уравнение (II.28), находим, что Gж = Gп = G
+
RT ln
p.
Дифференцируя это уравнение по внешнему давлению П, получим:
(∂G/∂П)T = RT(∂ ln p/∂П).
Согласно уравнению (II.38) (∂G/∂П)Т = V, где V - молярный объем жидкости, откуда ∂ ln p/∂П = V/RT.
118
При условии, что жидкость несжимаема, интегрирование этого уравнения в пределах от р1 до р
дает
р
=
p1eПV/RT.
Если раствор является разбавленным, то р1 = p
x1. Подставив это выражение в предыдущее уравнение, получим:

Для разбавленных растворов можно ограничиться первым членом разложения в ряд ln[1 + (n2/n1))] = n2/n1. При этом получим: ПVp = n2RT или П = c2RT, где Vp = n1V - объем растворителя, в котором находится n2 молей растворенного вещества; c2 = n2/Vp - концентрация.
Таким образом, между выражениями для осмотического давления разбавленного раствора и для давления идеального газа существует полное подобие. Этот факт был установлен Вант-Гоффом, указавшим, что осмотическое давление численно равно такому давлению, которое оказывало бы при данной температуре растворенное вещество в газообразном состоянии, если бы оно занимало объем раствора.
Следует, однако, заметить, что аналогия в свойствах разбавленных растворов и идеальных газов является далеко не полной, так как характер движения молекул растворенного вещества в жидкости значительно отличается от движения молекул газа.
Осмотическое давление характеризует тенденцию растворителя проникнуть в раствор или, наоборот, растворенного вещества распространяться в объеме растворителя. Ранее было показано, что аналогично расширению идеального газа эта тенденция обусловлена только увеличением энтропии, так как энергия при таком процессе остается постоянной.
Экспериментальные методы определения осмотического давления основаны на измерениях гидростатического давления столба жидкости, уравновешивающего стремление растворителя проникнуть через перегородку в раствор, подобно тому, как показано на рис. V.5.
Закон действующих масс для разбавленных растворов. Пусть вещества А, В и D находятся в растворе, т.е.
Aраствор + Bраствор = 2Dраствор.
Выражая химические потенциалы А, В и D согласно
119
уравнению (V.16), при равновесии получим:
ψ
+
RT ln
cA + ψ
+
RT ln
cB = 2ψ
+ 2
RT ln
cD,
где cA, cB и cD - концентрации. Отсюда.

Так как величины ψ0 зависят только от Т, то при постоянной температуре c
/(
cAcB) =
K.
Таким образом, для разбавленных растворов закон действующих масс применим в таком же виде, как и для идеальных газов. Для разбавленных растворов концентрации, выраженные различными способами, пропорциональны друг другу, поэтому при любом способе их выражения величина К остается постоянной. Разумеется, что как численные значения K, так и величины изменения энергии Гиббса при реакции (например, стандартные величины ΔG0) зависят от выбранных единиц концентрации. В качестве стандартных могут быть выбраны растворы различных концентраций, например моляльный, 1 % или 0,1 %-ный. Если концентрация выражается в массовом содержании, %, то часто ΔG0 относят к реакции в растворе, где все участники реакции имеют концентрации, равные 1 %, а остальное составляет растворитель. Закон действующих масс в приведенной выше форме применим и для реакции в системах, состоящих из нескольких фаз, если они являются разбавленными растворами. Например, важнейшая реакция сталеплавильного производства - обезуглероживание - протекает с участием двух жидких фаз (сталь и шлак) и газовой, т.е.
Cl + (FeO) = [Fe] + COг.
Выражая концентрации в массовых содержаниях, % и считая растворы в железе и FeO в шлаке разбавленными, найдем, что при равновесии

Принимая во внимание, что [Fe] −∼ 100, введем эту постоянную величину в константу равновесия, тогда K = рCO/[C](FeO). Оксид углерода может выделяться с достаточной скоростью из расплавленной стали, если ее давление близко к атмосферному. При высоких температурах и сильном перемешивании стали пузырями СО система металл-шлак-газ
120
близка к равновесию. При этих условиях величина [С] в "кипящей" ванне определяется концентрацией FeO в шлаке1.
В ряде случаев (например, при выплавке трансформаторной стали) необходимо достичь очень низкой концентрации углерода 0,002÷0,003 %. Из приведенного уравнения видно, что для этого следует понижать pCO Применение вакуумных печей в современной металлургии позволяет выплавлять железо и сталь с минимальным содержанием углерода.
Рассмотрим теперь реакцию, в которой наряду с разбавленным раствором участвуют вещества (одно или несколько) в твердом состоянии, например: Aт + Bраствор = Dраствор.
Энергия Гиббса твердого тела GA зависит только от температуры, поэтому при равновесии
GA + ψ
+
RT ln
cB = ψ
RT + ln
cD и
K =
cD/
cB.
Отсюда видно, что равновесие не зависит от количества твердого тела, представляющего собой избыточную фазу (концентрация А не входит в выражение для K).
Процесс растворения твердого тела в жидкости можно рассматривать как реакцию Aт = Aраствор.
Если образующийся раствор - разбавленный, то константа равновесия численно равна растворимости, т.е. K = cA.
В соответствии с этим зависимость растворимости от температуры может быть выражена уравнением:
d ln cA/dT = ΔH/RT2.
Если растворение сопровождается поглощением тепла ΔH > 0, то растворимость увеличивается при повышении температуры. Наоборот, если при растворении выделяется тепло, то растворимость уменьшается при повышении температуры.
Закон распределения. Рассмотрим процесс перехода вещества из одной фазы в другую. При равновесии оно распределяется между этими фазами, например, двумя несмешивающимися жидкостями в определенном отношении. Если оба раствора разбавленные, то химический потенциал вещества в первой и второй фазах выражается уравнением:
 (V.24)
(V.24)
121
При равновесии
μI = μII; ln(cI/cII) = (ψ
- ψ
)/
RT,
и, следовательно, при постоянной температуре отношение
сI/сII = L,
(V.25)
называемое коэффициентом распределения, является постоянной величиной, не зависящей от концентраций вещества в обеих жидкостях. Величины сI и cII могут изменяться (например, при удалении вещества или разбавлении), но их отношение при равновесии должно оставаться постоянным. Оно определяется природой растворителей и растворенного вещества и температурой. Последняя зависимость, как и для константы равновесия, определяется уравнением: d ln L/dT = ΔH/RT2, где ΔH - изменение энтальпии при переходе растворенного вещества из второй жидкости в первую.
Соотношение (V.25) является выражением закона распределения. Этот закон относится не только к распределению вещества между двумя жидкостями, но имеет значительно более общий характер. Так, рассмотренный выше закон Генри является частным случаем закона распределения вещества (между газом и жидкостью). Закон распределения был сформулирован и разработан В. Нернстом, А.А. Яковкиным, Н.А. Шиловым.
В форме, выражаемой уравнением (V.25), закон распределения справедлив, если растворенное вещество имеет одинаковую молекулярную массу в обеих жидкостях. В случае ассоциации или диссоциации так же, как и в выражении закона Генри, необходимо учесть изменение молекулярной массы растворенного вещества при переходе из одной фазы в другую. Если в первой жидкости она равна MI, а во второй MII, то уравнение (V.25) принимает следующий вид:
L = c
/
cII.
Как следует из приведенного вывода, закон распределения в виде уравнения (V.25) соблюдается лишь для разбавленных растворов. Известным примером применения этого закона является распределение иода в виде молекул l2 между водой (II) и несмешивающимся с ней четырех-хлористым углеродом (I):
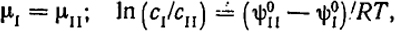
122
Закон распределения имеет большое значение для анализа металлургических процессов. Чугун и шлак, сталь и шлак, шлак и штейн представляет собой пары несмешивающихся жидкостей, между которыми распределяются различные растворяющиеся в них элементы или соединения. Это явление используют для рафинирования расплавленных металлов от вредных примесей. Например, для десульфурации стали широко применяют так называемые синтетические шлаки, состоящие в основном из СаО и А12О3. Коэффициент распределения серы LS в этом случае существенно превышает 100, т.е. при равновесии концентрация серы в жидкой стали в 100 раз меньше, чем в жидком шлаке. Металлургические шлаки представляют собой растворы, состоящие из различных оксидов (СаО, FeO, SiO2 и др.),а не однокомпонентную жидкость. Поэтому LS зависит от состава шлака.
Снижение концентрации серы в шлаке должно привести и к уменьшению ее содержания в стали. Например, путем увеличения количества жидкого шлака в печи или его скачивания с последующим наведением свежего шлака можно достаточно полно очистить сталь от серы. Закон распределения описывает также равновесие между разбавленными твердыми растворами или жидким и твердым растворами, например, распределение примесей между твердой и жидкой фазами при кристаллизации. Это явление эффективно используется для очистки материалов методом зонной плавки.
Быстрое развитие новых отраслей техники (атомная энергетика, полупроводниковая электроника, жаропрочные материалы) требует производства очень чистых металлов. О необходимой степени чистоты материалов, применяемых в ряде специальных случаев, можно судить по используемому для их оценки способу выражения концентрации - число атомов примеси на 106 атомов основного металла (р.р.т. - parts per million, т.е. число частей на миллион).
Естественно, что обычные методы выплавки и рафинирования не обеспечивают получения материалов со столь низкими концентрациями примесей. В связи с этим получили распространение новые способы производства, к числу которых относится выплавка металлов и сплавов в вакууме, рафинирование металла водородом для удаления из него следов углерода, серы, кислорода, электрошлаковый переплав и др.
Одним из наиболее эффективных методов глубокой
123
очистки материалов является зонная плавка, изобретенная в 1952 г. В. Пфаном. Метод основан на явлении распределения примеси между контактирующими в процессе плавления твердой и жидкой фазами. В этом случае закон распределения имеет вид: L = ст/сж, где ст и сж - концентрации примеси в твердой и жидкой фазах при равновесий.
Если L < 1, то при плавлении материала образующаяся жидкость обогащается примесью, а равновесная твердая фаза очищается от нее. В реальных условиях распределение примеси в соответствии с величиной L имеет место лишь в тонких слоях жидкой и твердой фаз, где успевает установиться равновесие. Вообще же распределение характеризуется величиной эффективного коэффициента L’, которая зависит от условий затвердевания и скорости перемещения зоны расплавленного металла.
Схематично процесс зонной очистки металлического стержня, содержащего равномерно распределенную примесь при концентрации c0, при помощи передвигающегося кольцевого нагревателя Н (например, индуктора высокочастотного генератора) показан на рис. V.6.
Сначала расплавляют узкую зону, совпадающую с левым концом стержня. Так как эта зона слева не контактирует с твердой фазой, то концентрация, примеси в ней остается с0. Незначительное передвижение нагревателя в правую сторону приведет к кристаллизации металла слева от нагревателя и перемещению расплавленной зоны в правую сторону. В первой порции затвердевшего металла концентрация примеси составит c = L’c0, и, так как L' < 1, она будет меньше исходной. Дальнейшее перемещение расплавленной зоны приводит к увеличению концентрации примеси в жидкости и накоплению примеси в правом конце стержня. Многократное прохождение зоны вдоль стержня приводит к глубокой очистке металла и достижению особых свойств. Примером может служить очистка германия, используемого в качестве полупроводникового материала. Присутствие в этом металле небольших количеств меди, железа, никеля резко изменяет его проводимость и делает непригодным для применения в радиотехнических устройствах. Очистка зонной плавкой снижает содержание указанных элементов до концентрации, меньшей, чем один атом примеси на 1010 атомов германия.
124
1
V - объем раствора, в котором при данной концентрации содержится 1 моль вещества 2, а в единице объема содержится 1/
V молей.
1
Так как
pCO = 1, то [С] [О] = const = 1/
K
