Парциальные молярные величины компонентов раствора взаимосвязаны. Так, если известна зависимость давления пара одного из компонентов бинарного раствора от его концентрации, то можно вычислить давление пара другого компонента. Это позволяет существенно сократить число экспериментальных определений, необходимых для термодинамической характеристики растворов.
Связь между парциальными молярными величинами можно найти следующим путем. Очевидно, при постоянных р и Т изменение какого-либо экстенсивного свойства раствора dg, например объема, не зависит от способа, которым осуществляется это изменение, т.е.
dg = (∂g/∂n1)n2,n3... dn1 + (∂g/∂n2)n1,n3... dn2 + ...
Согласно определению (∂g/∂ni)p,T,nj(j + i) = gi, поэтому
dg = g1dn1 + g2dn2 + ... .
(V.5)
Величина dg есть приращение свойства при добавлении к раствору молей компонентов 1, 2 .и т.д. в количествах, соответствующих dn1, dn2, ...
Чтобы найти величину самого свойства, следует провести интегрирование уравнения (V.5). Представим себе, что к данному раствору добавляются малые количества раствора такой же концентрации. Тогда величины g1, g2 ... не будут изменяться, и в этом случае после интегрирования уравнения
101
(V.5) получим:
g = g1n1 + g2n2 + ...,
(V.6)
где константа интегрирования, очевидно, равна нулю, так как при n1 = n2 = ... = 0 и g = 0.
Таким образом, любое экстенсивное свойство может быть найдено из свойств компонентов для любого раствора путем аддитивного сложения, если использовать не молярные, а парциальные молярные величины.
Если же одновременно изменять и количество, и состав раствора, то изменение свойства g можно найти дифференцированием уравнения (V.6):
dg = g1dn1 + n1dg1 + g2dn2 + n2dg2 + ...
(V.7)
Сопоставляя уравнения (V.5) и (V.7), найдем:
n1dg1 + n2dg2 + ... = 0,
(V.8)
или, разделив это уравнение на Φni, получим соотношение, в которое входят молярные доли:
x1dg1 + x2dg2 + ... = 0.
(V.9)
Уравнения (V.6), (V.8) и (V.9) носят название уравнений Гиббса-Дюгема. Они связывают парциальные молярные величины с составом раствора.
Разделив уравнение (V.9) на dх1 при постоянных р и Т, получим уравнение:
x1(∂gi/∂x1)p.T + x2(∂g2/∂x1)p.T = 0,
связывающее между собой парциальные молярные величины компонентов раствора. Оно может быть представлено в виде:
Φxi(∂gi/∂xi) = 0.
Для бинарного раствора х1 + х2 = 1 и dx1 = -dx2, поэтому
x1(∂g1/∂x1)p.T = x2(∂g2/∂x2)p.T.
Таким образом, если измерена величина g1 как функция х1, то можно рассчитать g2. Возьмем, например, в качестве парциальной молярной величины химический потенциал μi = μ
+
RT ln
pi, тогда из предыдущего уравнения следует
x1(∂ ln p1/∂x1)p.T = x2(∂ ln p2/∂x2)p.T.
(V.10)
102
Это важное уравнение связывает давление паров компонентов раствора и позволяет с помощью измеренных давлений пара одного компонента над раствором рассчитать давление пара второго компонента. Кроме того, важно, что уравнение (V.10) справедливо для любых растворов, и поэтому из него следует простой критерий, позволяющий оценить надежность экспериментальных измерений pi.
Для этого представим уравнение (V.10) в следующем виде:
 (V.11)
(V.11)
Производная ∂р2/∂х2 есть тангенс угла наклона касательной к кривой р2 - х2 в некоторой точке А, отвечающей раствору состава х2; p2/x2 есть наклон прямой, соединяющей точку А с началом координат. То же самое справедливо и для кривой р1 - х1. Поэтому, если, например, касательная к кривой р2 - х2 проходит через начало координат, т.е. ∂р2/∂х2 = р2/х2, то для раствора этого состава касательная к кривой р1 - x1 также должна проходить через начало координат, как это следует из уравнения (V.11).
Чтобы определить парциальную молярную величину данного компонента, необходимо найти зависимость соответствующего экстенсивного свойства от состава раствора при постоянных р, Т и числах молей остальных компонентов и произвести дифференцирование по числу молей этого компонента. Для бинарных растворов такое определение обычно проводится графически при помощи метода отрезков. Для этого вычисляют свойство одного моля раствора.
Молем раствора называется такое его количество, при котором число молей каждого компонента равно его молярной доле. Например, один моль раствора углерода в жидком железе, в котором xC = 0,1 и хFe = 0,9, содержит 0,1 моля углерода и 0,9 моля железа. Так как молярная масса углерода равна 12, а железа 55,85 г, то масса одного моля такого раствора составит 12,0 - 0,1 + 55,85 - 0,9 = 51,465 г.
Свойство раствора g, относящееся к одному молю, обозначается индексом m. Например, объем одного моля раствора обозначается Vm.
Метод отрезков состоит в следующем. Из уравнения (V.5) для одного моля раствора (dgm = g1dx1 + g2dx2) и из условия dx1 = -dx2 следует, что
g2 - g1 = dgm/dx2.
103
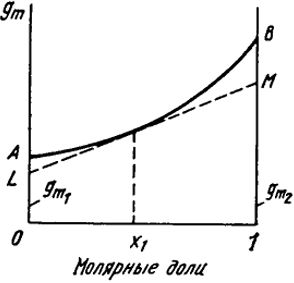
Рис. V.1. К понятию о парциальных молярных величинах
Согласно уравнению (V.6) также для одного моля раствора
g1 = (gm - g2x2)/(1 - x2).
Подставляя это выражение g1 в предыдущее найдем:
g2 = gm + (1 - x2)
;
(V.12)
g1 = gm - x2
.
(V.13)
Графическое построение для определения парциальных молярных величин представлено на рис. V.1.
Ось абсцисс, на которой откладываются молярные доли первого и второго компонентов (х1 и х2), ограничена условием x1 + x2 = 1. Точка 0 соответствует первому чистому компоненту; здесь x1 = l и x2 = 0; точка 1 характеризует второй чистый компонент (х2 = 1 и x1 = 0). Каждая точка на прямой 0-1 соответствует раствору определенного состава.
Величина какого-либо свойства одного моля раствора gm. (например, объем Vm) откладывается на оси ординат. Кривая АВ выражает зависимость свойства от состава раствора. Если при образовании раствора его свойство аддитивно складывается из свойств компонентов, то вместо кривой зависимость будет выражаться прямой линией. Отрезки 0А и 1В представляют собой соответственно молярные свойства чистых компонентов g
и
g
. Из уравнений (V.12) и (V.13) следует, что отрезки на осях ординат (при
х1 = 1 и
x2 = 1), отсекаемые касательной
LM к кривой
АВ, проведенной, например, в ординате, соответствующей составу раствора
х1, равны
g1 и
g2.
Зависимости парциальных молярных величин от концентрации могут иметь сложный характер, как это показано на рис. V.2 для молярных объемов жидкого сплава, кадмия с магнием. Изменение этих величин для одного моля сплава описывается кривой с максимумом и минимумом.
Пунктирная прямая, которая соединяет точку, соответствующую молярному объему чистого кадмия V
=
104
= 13,2 см3/моль, с точкой для чистого магния V
= 13,52 см
3/моль, отвечает идеальному случаю, когда при образовании раствора соблюдается аддитивность и при всех концентрациях Δ
V = 0.
Как видно из рис. V.2, сплавы Cd - Mg, за исключением области до Mg = 0,l, образуются с уменьшением объема. Так, для сплава xMg = 0,3 ΔV = -0,43 см3/моль. Для этого сплава парциальные молярные объемы, определяемые

Рис. V.2. Молярные объемы жидких сплавов магния и кадмия
по отрезкам на осях координат, отсекаемых касательной (штриховая линия A), составляют VCd = 13,1 см3/моль и VMg = 11,9 см3/моль. Объем всего сплава близок к 12,65 см3/моль. В соответствии с уравнением (V.6) он должен составить Vm = 13,1·0,7 + 11,9·0,3 = 12,64 см3/моль.
105
