Принятый в настоящее время метод расчета равновесий с помощью третьего закона термодинамики основывается на определении абсолютных энтропии всех участвующих в реакции веществ. Он полностью вытеснил метод "химических постоянных", существовавший ранее.
В методе абсолютных энтропии константа равновесия химической реакции и, следовательно, ее выход вычисляются из уравнений:
ΔG0 = -RT ln Kp и ΔG0 = ΔH0 - ТΔS0.
Таким образом, задача сводится к нахождению теплового эффекта реакции (ΔH0) и изменения энтропии реакции (ΔS0).
Для решения первой части этой задачи требуется знание температурной зависимости изменения ΔCp реакции и величины ΔH0 при одной температуре, что позволяет при помощи уравнения Кирхгофа вычислить постоянную ΔH
и тем самым Δ
H
, при любой температуре (см. гл.1).
Решение второй части задачи требует знания абсолютных величин энтропии. Так, например, в общем виде для реакции A + B = 2D ΔS0 = 2S
-
S
-
S
.
Значение третьего закона термодинамики для расчетов равновесий состоит в том, что он. дает возможность найти величины энтропии участвующих в реакции веществ (S
,
S0 |
A,
S
). Поскольку энтропия чистого кристаллического вещества при абсолютном нуле равна нулю, то при любой другой температуре ее значение может быть найдено из уравнения (IV.3), т.е.
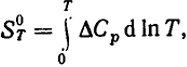
если имеются точные данные о теплоемкостях при низких температурах.
Методы таких измерений основаны на применении калориметров, помещаемых в вакуумные оболочки, уменьшающие потери тепла вследствие теплопроводности. В калориметр вводится точно измеряемое весьма малое количество тепла путем пропускания электрического тока. При помощи большого числа последовательно соединенных термопар или чувствительного термометра сопротивления измеряется соответствующее малое повышение температуры. Теплоемкости
89
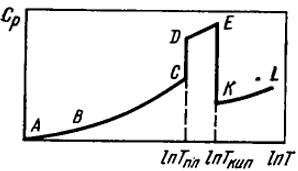
Рис. IV.2. Графическое определение энтропии
измеряются до температур, близких к абсолютному нулю.
Интегрирование уравнения (IV.3) обычно проводится графическим методом путем построения кривой в координатах Ср - ln Т, как это показано на рис. IV.2. Отрезок кривой ВС представляет экспериментальные величины теплоемкостей вещества в твердом состоянии. Точка В соответствует наиболее низкой температуре, при которой для данного вещества возможны надежные измерения теплоемкостей (обычно 10-15 К).
Теплоемкость при более низких температурах, приближающихся к абсолютному нулю (отрезок кривой АВ), может быть удовлетворительно вычислена по уравнению Дебая, согласно которому она в этой области пропорциональна третьей степени абсолютной температуры (вывод уравнения Дебая приводится в гл. XII). Так как теплоемкости твердых тел ниже 10 К очень быстро уменьшаются с изменением температуры, эта часть кривой оказывает небольшое влияние на точность окончательного результата. Площадь, ограниченная кривой ABC, осью ln T и ординатой, соответствующей значению Tпл, дает величину энтропии твердого тела при этой температуре. Точка С соответствует температуре плавления твердого тела, при которой происходит резкое увеличение теплоемкости, и отрезок DE представляет теплоемкость жидкости. При плавлении происходит поглощение тепла ΔHпл, приводящее к увеличению энтропии на величину ΔSпл = ΔHпл/Tпл.
Точка Е соответствует температуре кипения жидкости при атмосферном давлении. Площадь, ограниченная кривой DE и ординатами температур плавления и кипения, дает увеличение энтропии при нагревании жидкости между этими температурами. При температуре кипения происходит резкое уменьшение теплоемкости до величины, соответствующей теплоемкости газа (точка К). При испарении энтропия возрастает на величину ΔSисп = ΔHисп/Tкип. Дальнейшее увеличение энтропии газа определяется величиной площади, лежащей под кривой KL. В случае, если в твердом состоянии тело претерпевает полиморфное превращение, то также необходимо учесть соответствующее увеличение энтропии: ΔSпревр = ΔHпревр/Тпревр.
90
Вычисление абсолютной величины энтропии можно пояснить на примере азота.
От 0 до 10 К значение S, полученное по уравнению Девая, 1,916 Дж/(моль·К). От 10 до 35,61 К для твердого азота графическое интегрирование дает 25,246 Дж/(моль·К). При температуре 35,61 К твердый азот претерпевает полиморфное превращение ΔH = 228,907 Дж/моль, и ΔS = 228,907/35,61 = 6,42 Дж/моль·К. От 35,61 К до температуры плавления 63,14 К (из графического интегрирования) ΔS = 23,384 Дж/(моль·К). Теплота плавления азота составляет 720,903 Дж/моль, откуда ΔSпл = 720,903/63,14 = 11,418 Дж/(моль·К).
От температуры плавления до температуры кипения (77,32 К) графическое интегрирование дает 11,414 Дж/(моль·К). Так как теплота испарения жидкого азота равна 5576,854 Дж/моль, то увеличение энтропии при испарении составит 5576,84/77,32 = 72,128 Дж/(моль·К).
Суммирование всех приведенных выше величин дает энтропию моля газообразного азота при 77,32 К и давлении, равном 1 атм, S
= 151,933 Дж/(моль·К). Заметим, что в приведенном расчете фигурируют не только термические величины, но и равновесные, а именно температуры плавления и кипения. Однако их определение не связано со значительными экспериментальными трудностями.
Таким образом, энтропии всех веществ могут быть найдены из термических данных. Этим открывается принципиальная возможность только при помощи калориметрических измерений найти условия равновесия для любой реакции. Покажем схему такого расчета на примере реакции: FеС12ж + Н2г = 2НClг + Fет.
Определим выход реакции при 800 К. Необходимые для решения задачи данные следует брать из справочников и таблиц стандартных величин, а недостающие должны определяться из калориметрических опытов.
Для рассматриваемой реакции сначала найдем энтальпии образования FеСl и НСl при комнатной температуре (298 К) и из них вычислим значение ΔH
реакции.
Затем находим выражение для температурной зависимости ΔCp и по уравнению Кирхгофа с использованием ΔH
вычисляем Δ
H
.
Способом, который был проиллюстрирован выше на примере азота, вычисляются абсолютные энтропии FeCl, H2, HCl и Fe при 800 К и составляется уравнение:
ΔS
= 2
S
(HCl) +
S
(Fe) -
S
(FeCl
2) -
S
(H
2).
Константа равновесия находится из соотношения:
ΔG
= Δ
H
- 800Δ
S
= -19,14·800 lg
Kp,
а затем определяется выход реакции.
Как отмечалось выше, третий закон термодинамики позволяет найти постоянную интегрирования в уравнении (IV.1).
Рассмотрим для этого сначала реакции между конденсированными
91
фазами. В этом случае вблизи абсолютного нуля экспериментально достигается состояние вырождения, в котором свойства тел не зависят от температуры, в частности в этой области ΔH0 = ΔH
. Учитывая это, из уравнения (IV.1) получим:
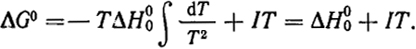
Продифференцируем это уравнение по температуре в области вырожденного состояния:

Согласно уравнениям (IV.4) и (IV.5) вблизи абсолютного нуля обе производные последнего уравнения обращаются в нуль и, следовательно, I = 0.
Этот вывод очень важен, так как он устраняет неопределенность в уравнении для энергии Гиббса при реакциях между конденсированными телами и дает возможность расчета соответствующих равновесий. При этом уравнение (IV.1) упрощается:
ΔG0 = -T∫
dT.
(IV.6)
Поскольку это уравнение справедливо для любой температуры, то величина ΔH0, стоящая под знаком интеграла, должна рассматриваться как функция температуры. Очевидно также, что практическое использование уравнения (IV.6) для расчетов возможно лишь при условии, что известны теплоемкости участвующих в реакции веществ вплоть до температур, близких к абсолютному нулю.
Для газов температурная зависимость теплоемкостей в области вырождения не поддается экспериментальному измерению, что приводит к неприменимости уравнения (IV.6) к реакциям с участием газов.
В ряде случаев при расчетах равновесий при помощи третьего закона термодинамики полезно использовать различные закономерности, позволяющие приближенно оценивать величины, которые экспериментально не определены и отсутствуют в справочниках.
В.А. Киреев показал, что энтропия образования соединений из атомов ΔS
зависит главным образом от числа атомов в молекуле и для однотипных соединений приблизительно одинакова. Определение величины Δ
S
для соединения, например, вольфрамата какого-либо двухвалентного металла, может быть осуществлено путем комбинирования
92
следующих реакций:
Meг + 1/2O2г = MeOт;
(1)
Wг = Wт;
(2)
Wт + 3Oг = WO3т;
(3)
4Oг = 2Oг;
(4)
MeOт + WO3т = MeWO4т;
(5)
Meг + 4Oг + Wг = MeWO4т
(6)
Таким образом, ΔS
= Δ
S
= Δ
S
- Δ
S
+ Δ
S
+ Δ
S
+ Δ
S
. Близость величин Δ
S
для ряда вольфраматов и молибдатов была показана Я.И. Герасимовым с сотрудниками. Найденные ими значения Δ
S
Дж/(моль·К) при 1273 К представлены ниже:
| CaWO4 |
MgWO4 |
MnWO4 |
FeWO4 |
NiWO4 |
CaMoO4 |
SrMoO4 |
ZnWO4 |
PbWO4 |
| 851,0 |
899,1 |
827,6 |
825,9 |
899,6 |
848,1 |
824,2 |
804,2 |
836,0 |
Таким образом, величина ΔS
для указанных соединений колеблется в пределах 800 = 900 Дж/(моль·К), т.е. в пределах, указываемых В.А. Киреевым для веществ, молекулы которых состоят из шести атомов.
Основываясь на экспериментальных данных о величинах ΔS
, В.А. Киреев предложил метод однотипных реакций, в которых каждому участнику одной реакции соответствует участник другой, имеющий такое же строение и находящийся в таком же агрегатном состоянии. Примером однотипных реакций могут служить процессы диссоциации карбонатов, сульфатов, оксидов металлов одной и той же валентности:
| СаС03т = СаОт + СО2Г; |
MgCO3T = MgOT + СО2г. |
| SrCO3T = SrOT + СО2Г; |
ВаСО3т = ВаОт + СО2Г. |
Для подобных однотипных реакций близки не только величины ΔS
, но и Δ
S0. Отсюда следует, что для таких реакций близки и величины (∂Δ
G/∂
T)
p и соответственно коэффициенты при температуре в степенных уравнениях для теплоемкости. Для каких-либо двух однотипных реакций (1) и (2) получаем путем почленного вычитания уравнений для энергии Гиббса при данной температуре:
ΔG
= Δ
H
-
TΔ
S
93
ΔG
= ΔH
- TΔS
ΔG
- Δ
G
= Δ
H
- Δ
H.
Последнее соотношение позволяет рассчитать энергию Гиббса неизученной реакции, например ΔG
, по известным значениям энтальпий Δ
H
и Δ
H
и Δ
G.
К описанному выше методу примыкает и предложенный М.X. Карапетянцем способ приближенного расчета энтропии при помощи уравнения: (S
)
2 =
A(
S
)
1 +
B.
Величины А и В являются постоянными и характеризуют соотношение между энтропиями веществ, принадлежащих к двум группам подобных соединений, например, оксидам (S
) и фторидам (
S
) щелочноземельных металлов. Таким образом, зная, например, энтропию СаО, можно вычислить соответствующую величину для СаF
2, если она не известна.
В современных справочниках термодинамических величин наряду с таблицами значений ΔG0, ΔH0 и ΔS0 широкое распространение получило табулирование величин функции Φ, которая называется приведенной энергией Гиббса и определяется уравнением Φ = (G
-
Н
)/
T. Выражение для расчета этой функции получается из уравнения (II.38), если вычесть из обеих его частей тождество d(
H
/
T) =
H
d(1/
T), т. e.
d(G/T) = H
d(1/T)
 (IV.7)
(IV.7)
где H
- энтальпия данного вещества при абсолютном нуле. При интегрировании уравнения (4.7) от 0 К до заданной температуры
Т получаем:
 (IV.8)
(IV.8)
Из уравнения (II.24) следует, что (G - H)/T = -S и, согласно третьему закону термодинамики, вблизи T = 0 К она обращается в нуль. Поэтому
94

поскольку H
-
H
=
Cpd
T. Таким образом, функцию Φ для данного вещества можно вычислить, если известна его теплоемкость от 0 К до
Т, что и используется при составлении таблиц.
При протекании физического процесса или химической реакции изменение функции Φ определяется разностью между соответствующими величинами для продуктов реакции и исходных веществ:
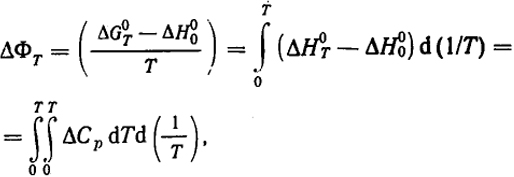 (IV.9)
(IV.9)
где ΔH
- изменение энтальпии при процессе, протекающем при 0 К. Так как Δ
G
, то из уравнения (IV.9) следует, что
lgKp = -ΔΦт/19,14 - ΔH
/ 19,14T.
(IV.10)
Поясним это расчетом равновесия реакции: Сграфит + Н2Ог = СОг + Н - Hrr при 1000 К. При этой температуре, согласно таблицам1, величины Φ для Cграфит; Н2Ог; СОГ и Н2г соответственно составляют: -11,594; -196,690; -204,430 и -136,976 Дж/(моль·К) и, следовательно:
ΔΦ = -204,430 - 136,976 - (-196,690 - 11,594) = -133,344 Дж/(моль·К.)
В таблицах также приводятся значения энтальпий, из которых можно вычислить ΔH
, если известно Δ
H
так как из уравнения Кирхгофа следует, что Δ
H
= Δ
H
+ Δ(Δ
H
-
H
). Величины Δ
H
образования для участвующих в рассматриваемой реакции веществ С
графит; Н
2О
Г; СО
Г и Н
2г- соответственно составляют: 0; -238923; -113813 и 0 Дж/моль. Отсюда для реакции Δ
H
= -113813 - (-238923) = 125109 Дж/моль.
Следовательно, согласно уравнению (4.10)
lgKp = -(-
) - (
) −
∼ 0,40 и
Kp −
∼ 2,5
95
Заметим, что подобным образом составляются таблицы для расчетов давления пара, т.е. равновесий конденсированная фаза - газ. При этом табулируются функции G
-
H
, находят значения теплоты испарения или сублимации Δ
H
. Окончательный расчет ведется по уравнению:
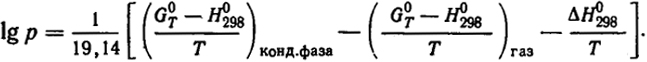
96
1
В существующих таблицах величины Φ в большинстве случаев приводятся в кал.
