Основное уравнение для определения энтропии dS = δQ/T является дифференциальным, поэтому в выражение для энтропии входит постоянная интегрирования. Из этого следует, что на основании первого и второго законов термодинамики невозможно определить абсолютное значение энтропии. Такая неопределенность энтропии отражается и на уравнениях, из которых могут быть найдены условия
82
равновесия химических реакций. Это относится к уравнению ΔG0 = ΔH0 - ТΔS0 и уравнению Гиббса-Гельмгольца d(ΔG0/T)/dT = -ΔH0/T2 или эквивалентному ему уравнению изобары dlnKp/dT = ΔH0/RT2.
Действительно, как отмечалось в гл. III, при интегрировании этих уравнений появляется неопределенная постоянная интегрирования I:
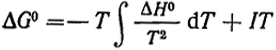 (IV.1)
(IV.1)
или
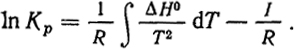 (IV.2)
(IV.2)
Вследствие этого вычисления величин ΔG0 и Кp не могут быть доведены до численных значений, даже если полностью известна температурная зависимость ΔH0, благодаря измерениям теплоемкостей участников реакции вплоть до температур, близких к абсолютному нулю. Возникающая из-за величины I неопределенность иллюстрируется рис. IV.1. Зависимость ΔH0 = f(T), вытекающая из измерений термических величин и описываемая формулой Кирхгофа (I.27), представлена сплошной кривой. Зависимость же ΔH0 = φ(T) показана несколькими пунктирными линиями, положения которых зависят от значения I.
Из уравнения ΔG = ΔH0 - TΔS0 следует, что при температуре, близкой к абсолютному нулю, ΔG0 = ΔH0, так как величина ΔS0 реакции не может быть бесконечностью. Действительно, так как S = k ln ω, то энтропия не может неограниченно возрастать, поскольку вероятность состояния не может быть равной бесконечности. Таким образом, кривые ΔH0 = f(T) и ΔG0 = φ(T) исходят из одной точки. Для того чтобы определить положение кривой, выражающей температурную зависимость изменения энергии Гиббса при реакции, очевидно, требуется знание величины I.
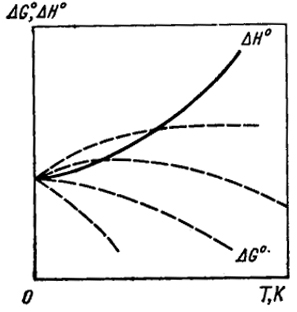
Рис. IV.1. Зависимости Δ
H0 и Δ
G0 химической реакции от температуры
83
Эта величина, как уже отмечалось в гл. III, может быть определена эмпирическим путем (по данным для ΔG0 или Кp при одной температуре). Возникает вопрос, нельзя ли найти I теоретически, исходя из представлений о существовании какого-либо свойства, общего для всех тел?
Действительно, по мере приближения к абсолютному нулю свойства тел все менее зависят от температуры. Тело, свойства которого при данной точности опыта не зависят от температуры, называют вырожденным.
Опыт показывает, что вблизи абсолютного нуля вообще все термические коэффициенты, выражающие зависимость свойств тела от температуры, стремятся к нулю. В вырожденном состоянии тела как бы теряют связь с миром тепловых явлений. Область температур, в которой наступает вырождение, различна для разных тел. Так, для. алмаза состояние вырождения достигается уже при довольно далекой от абсолютного нуля температуре (∼90К). Это означает, что ниже 90 К, при любой температуре, например при 10 или 70 К, свойства алмаза (объем, энергия и др.), зависящие от температуры, будут иметь в пределах существующей точности измерений одинаковые значения. В противоположность алмазу свинец переходит в вырожденное состояние при очень низких температурах.
Следует подчеркнуть, что понятие о вырожденном состоянии противоречит представлениям механики. Рассмотрим, например, алмаз при 10 К, приведенный в соприкосновение с газом, имеющим температуру 80 К. При этом молекулы газа не передадут свою энергию в какой-либо заметной степени алмазу. Это противоречит механике, так как при столкновениях молекул газа и атомов углерода не происходит передачи энергии.
Это явление получает свое объяснение только на основе законов квантовой механики, которая устанавливает, что при периодическом движении энергия микрочастиц не может иметь любые значения, а изменяется строго определенными порциями - квантами. Так, например, электроны в атоме могут иметь лишь определенные состояния, в которых они обладают различными энергиями, отличающимися друг от друга на дискретные величины.
Колеблющаяся частица - осциллятор, как это будет подробно рассмотрено в гл. XII, может иметь различные уровни энергии, при этом расстояние между двумя соседними уровнями составляет постоянную величину hν, где
84
h - постоянная Планка, 6,62·10-27 эрг·с; ν - частота колебания.
В твердом кристаллическом теле молекулы (атомы или ионы) совершают упругие тепловые колебания около своих положений равновесия. Частота колебания определяется постоянной упругости и массой частицы. Расстояния между соседними энергетическими уровнями будут тем больше, чем выше частота колебания. Очевидно, разница между выводами классической и квантовой механики будет проявляться при низких температурах, при которых средняя энергия теплового движения молекул сравнима с величиной hv.
В теле, пришедшем в вырожденное состояние, практически все частицы находятся на самом низком энергетическом уровне, и если его привести в контакт с другим телом, например газом, у которого средняя энергия частиц значительно меньше, чем величина кванта, то передачи энергии между телами происходить не будет. Это является следствием конечной величины значения разностей между энергетическими уровнями атомов в твердом теле. Если бы рассматриваемое тело подчинялось законам классической механики, то его энергия могла бы изменяться непрерывно. Таким образом, явление вырождения является следствием квантовых законов.
Очевидно, что у алмаза вследствие большой величины упругой постоянной и малой массы атомов частоты колебаний ν и, следовательно, расстояния между энергетическими уровнями hν велики. Поэтому алмаз - тело, которое легче других приходит в состояние вырождения. Наоборот, мягкий, легко деформируемый свинец, состоящий из тяжелых атомов, характеризуется малой величиной ν и не достигает вырожденного состояния вплоть до 2 К.
В зависимости от кристаллической структуры и массы частиц различные тела характеризуются, разными температурами перехода в вырожденное состояние. Явление вырождения, наблюдающееся у всех тел, отражает общее для всех тел свойство. Это позволяет считать, что может быть выведен новый общий принцип, который даст возможность определить значение константы интегрирования I в уравнениях (IV.1) и (IV.2). Таким принципом является третий закон термодинамики, к формулировке которого впервые пришел В. Нернст. Он, однако, исходил не из общих принципов, а из опытных данных, согласно которым при реакциях в конденсированных системах разница
85
между ΔG0 и ΔH0 уменьшается с понижением температуры, приближаясь к нулю вблизи абсолютного нуля.
Первое утверждение третьего закона термодинамики состоит в том, что при приближении температуры к абсолютному нулю величины теплоемкостей (Ср и Cv) всех тел становятся равными нулю. Это соответствует тому, что в вырожденном состоянии внутренняя энергия и энтальпия тел не зависят от температуры, так как Cv = (dU/dT)V и Cp = (dH/dT)p.
Это утверждение основывается на результатах многочисленных измерений теплоемкостей при низких температурах. В рамках термодинамики оно принимается как аксиоматическое.
Как указывалось выше, при низких температурах величины термодинамических функций не зависят от температуры. В частности, это относится к энергии Гиббса, откуда следует, что (∂G/∂T)p = Q. Следовательно, согласно уравнению (II.34) S = -(∂G/∂T)p = 0.
Второе утверждение третьего закона состоит в том, что энтропия простых кристаллических тел стремится к нулю при приближении температуры к абсолютному нулю.
Эти два утверждения и являются выражением третьего закона термодинамики.
Следует отметить, что оба указанных утверждения не являются независимыми друг от друга, так как из второго может быть выведено первое. Энтропия может достигнуть нулевого значения лишь при условии, что теплоемкость обращается в нуль, как это следует из уравнения (II.45), поскольку
S =
(Cp/T)dT.
(IV.3)
Если Ср при T → 0 не стремится к нулю, то энтропия будет бесконечно велика.
Обычно при изложении третьего закона термодинамики ограничиваются вторым утверждением, известным как формулировка Планка. Однако следует отметить, что первое утверждение не имеет исключения и в равной степени относится к газам, твердым телам, жидкостям и растворам. Второе утверждение, как указывалось, относится к кристаллическим телам и неприменимо к растворам, переохлажденным жидкостям и некоторым веществам в твердом состоянии, например Н2, СО, NO.
В кристаллических телах молекулы (атомы или ионы)
86
совершают тепловые колебания около своих положений равновесия. При относительно высоких температурах молекулы (атомы) тела находятся на различных энергетических уровнях. Распределение молекул (атомов) тела по энергетическим уровням может осуществляться различным числом способов (ω).
Энтропия тела может быть вычислена по уравнению S = k ln ω. При приближении температуры к абсолютному нулю в вырожденном состоянии практически все молекулы переходят на самый низкий энергетический уровень и число способов осуществления данного состояния стремится к единице и, следовательно, величина энтропии - к нулю.
В случае твердого раствора даже при абсолютном нуле возможны различные способы осуществления состояния вследствие перестановки молекул различных компонентов растворов на место друг друга. Поэтому энтропия твердых растворов при абсолютном нуле отлична от нуля, в то время как теплоемкость обращается в нуль. Следовательно, твердые растворы не находятся в состоянии истинного равновесия при абсолютном нуле и должны были бы распадаться на составляющие их компоненты. Этого, однако, не происходит из-за малой подвижности частиц вблизи абсолютного нуля.
Для некоторых твердых тел, состоящих из несимметричных двухатомных молекул, например СО, при достаточно низких температурах утрачивается свободное вращение молекул и они все ориентируются вдоль некоторой оси. При этом для каждой молекулы возможны два положения:
и
. Так как минимуму энергии всего кристалла соответствует некоторая ориентация различных молекул, то при достаточно низкой температуре все молекулы должны определенным образом ориентироваться. Однако вследствие малости энергии, выигрываемой при этом, процесс должен осуществляться лишь при очень низких температурах, где практически он не идет из-за малой скорости. Таким образом, при низких температурах происходит закалка состояния, в котором сохраняются обе ориентации молекул.
Так как каждая молекула имеет два возможных способа расположения, то для моля число способов осуществления состояния
ω = 2NA и S = k ln 2NA или S = R ln 2.
87
Таким образом, энтропия СО стремится при приближении к абсолютному нулю к величине Rln2, равной 5,73 Дж/(моль·К). Подобное явление наблюдается в случае некоторых жидкостей, которые ниже температуры плавления переходят не в кристаллическое состояние, а в стеклообразное, имеющее энтропию большую нуля вблизи 0 К. Хотя стеклообразное состояние характеризуется более высокой энергией Гиббса, оно не превращается в кристаллическое из-за медленного установления равновесия при низких температурах. Оно становится "замороженным". Таким образом, отличие от нуля калориметрически измеряемой энтропии "замороженных" тел не противоречит третьему закону, а обусловлено тем, что они не находятся в состоянии термодинамического равновесия.
Из приведенных выше двух положений третьего закона термодинамики следует, что для химических реакций вблизи абсолютного нуля должны иметь место ΔСp = 0 и ΔS = 0.
Сопоставляя первое равенство с уравнением Кирхгофа: dΔH/dT = ΔCp, а второе - с уравнением (dΔG/dT)p = -ΔS, находим, что
 (IV.4)
(IV.4)
 (IV.5)
(IV.5)
Это означает, что кривые, выражающие зависимость ΔH и ΔG от температуры (см. рис. IV.1), должны иметь вблизи абсолютного нуля общую касательную, параллельную оси температур. Эти положения были выдвинуты Нернстом в 1906 г. в виде постулатов, на которых основывалась "тепловая теорема". Как отмечалось выше, он исходил из экспериментальных данных, указывающих, что по мере понижения температуры величины ΔH и ΔG для химических реакций приближаются друг к другу.
Принятая в настоящее время формулировка III закона термодинамики согласно Планку для любого индивидуального кристаллического вещества соответствует условиям: S = 0; Ср = 0 при T → 0.
Ниже будет показано, что этот принцип в виде уравнений (IV.4) и (IV.5) достаточен для определения константы интегрирования в уравнениях (IV.1 и IV.2) и, следовательно, для полного расчета равновесий по термическим данным.
88
