Вновь рассмотрим реакцию: A + 2B = 3D. При равновесии изменение энергии Гиббса равно нулю. Если ΔG < 0, то реакция должна протекать в сторону образования соединения D, а если ΔG > 0, то будет происходить его диссоциация.
Каково будет изменение энергии Гиббса при протекании реакции, когда в смеси исходные вещества находятся при некоторых произвольных парциальных давлениях ра, а образующийся продукт - при pd?
Так же, как в предыдущем параграфе, найдем выражение для величины ΔG, вычитая из энергии Гиббса продукта сумму энергий Гиббса исходных веществ, т.е.
ΔG = 3G
+ 3
RT ln
pd - (
G
+
RT ln
pa) - (2
G
+ 2
RT ln
рb)
или
ΔG = ΔG + RT ln (p
/ pap
).
(III.16)
Для того чтобы найти величину ΔG0, допустим, что выбранные парциальные давления соответствуют состоянию равновесия. В этом случае ΔG = 0, а отношение p
(
pap
) есть константа равновесия
Кp и, следовательно,
ΔG0 = -RT ln Kp.
(III.17)
Подставляя это значение в уравнение (III.17), получим:
ΔG = -RT ln Kp.
(III.18)
Это важное уравнение, найденное Вант-Гоффом, позволяет вычислить изменение энергии Гиббса при химической реакции. Оно называется уравнением изотермы химической реакции.
Уравнение изотермы показывает, что изменение энергии Гиббса реакции определяется соотношением двух членов, когда первый зависит от химической природы участвующих в реакции веществ, а второй от их концентрации. Рассмотрим влияние последних.
Пусть первоначальные парциальные давления в исходной смеси таковы, что p
= (
pap
) =
Кр, то величина Δ
G = 0, и реакция в этом случае не пойдет. Если же в смеси величина
p
будет настолько больше
раp
, что абсолютная величина второго члена правой части уравнения (III.18) станет больше первого, то Δ
G > 0, и реакция должна протекать
68
справа налево. Наоборот, при больших значениях ра и рb и малом рd величина ΔG отрицательна, и должно происходить образование D.
Таким образом, уравнение (III.18) показывает, что величина ΔG есть мера химического сродства, т.е. характеризует тенденцию веществ самопроизвольно реагировать друг с другом и образовывать продукты реакции.
Из сказанного следует, что химическое сродство зависит не только от природы веществ и температуры, но и от их парциальных давлений. При изменении парциальных давлений в исходной смеси газов величина ΔG может изменяться от +∞ до -∞, проходя через нулевое значение при равновесии.
Во второй половине XIX в. Бертло и Томсен стали широко использовать калориметрию для определения теплот химических реакций. Независимо друг от друга они выдвинули принцип: из числа возможных реакций происходит та, которая сопровождается наибольшим выделением тепла. Иными словами, согласно этому принципу мерой химического сродства, является количество выделяющегося при реакции тепла и самопроизвольно могут протекать только экзотермические реакции.
Однако принцип Бертло - Томсена противоречит термодинамике и самому факту существования химического равновесия. Как было показано выше, в зависимости от соотношения между концентрациями реагирующих веществ реакция может самопроизвольно протекать как в прямом, так и в обратном направлениях. При этом в одном случае она будет сопровождаться выделением тепла, а в другом - его поглощением. Экзотермические реакции, например, образования сульфидов переходных металлов, при относительно низких температурах идут практически до конца, а при высоких температурах происходит диссоциация этих соединений. Принципу Бертло-Томсона также противоречит существование самопроизвольных процессов, сопровождающихся поглощением тепла, например, растворение многих солей в воде. Следовательно, величина изменения ΔH реакции не может служить мерой химического сродства. Такой мерой является величина ΔG, определяемая уравнением: ΔG = ΔH - TΔS, где ΔH и ΔS - изменения энтальпии и энтропии реакции.
При низких температурах или при реакциях, сопровождающихся малым изменением энтропии (реакции между конденсированными фазами или с небольшим изменением числа молей газов), вклад произведения TΔS в величину ΔG невелик. Поэтому изменения энергии Гиббса и энтальпии реакции близки по величине и одинаковы по знаку, т.е. ΔG −∼ ΔH. В таких случаях принцип Бертло - Томсена позволяет сделать качественно правильные выводы. Этим объясняется то, что несмотря на его ошибочность указанным принципом в течение многих лет руководствовались в химии и в металлургии. При высоких температурах (и большие ΔS) разница между ΔG и ΔH может быть настолько большой, что знаки этих величин будут противоположными, и в этом случае принцип Бертло-Томсона приведет к ошибочным выводам.
При рассмотрении равновесий имеет значение особый случай, когда взятые исходные вещества реагируют в своих стандартных состояниях при парциальных давлениях
69
равных атмосферному, с образованием продуктов также в стандартных состояниях. Из уравнения (III.18) следует, что при этом ΔG0 = -RT ln Kp.
В этом случае величина ΔG0 называется стандартным или нормальным изменением энергии Гиббса. Таким образом, между стандартным изменением энергии Гиббса и константой равновесия существует непосредственная связь. Ввиду этого целесообразно составление таблиц величин ΔG0 для реакций образования соединений из простых веществ. Эти таблицы, как и таблицы тепловых эффектов (энтальпий), позволяют из относительно небольшого числа данных находить величины ΔG0 и, следовательно, константы равновесия для многочисленных реакций.
В существующих таблицах приведены стандартные изменения энергий Гиббса при температуре 25° C. При этом для всех элементов в стандартном состоянии величины ΔG0 приняты равными нулю. Такое условие вызвано тем, что для определения Кp существенно лишь изменение энергии Гиббса, поэтому выбор начала отсчета не имеет значения.
Рассмотрим некоторые примеры использования таблиц стандартных величин для расчетов равновесий.
Для водяного пара величина ΔG
= -228596 Дж/моль, характеризует изменение энергии Гиббса при реакции: Н
2г + 1/2О
2Г = Н
2О
г. Повторим, что для Н
2г и 0
2г, как для веществ, находящихся в стандартном состоянии, соответствующие величины Δ
= 0. В рассматриваемом случае изменение энергии Гиббса при образовании Н
2O
Г из элементов большая отрицательная величина. Отсюда следует, что константа равновесия должна быть очень велика, а равновесие практически полностью сдвинуто в сторону образования водяного пара. Действительно, используя уравнение Δ
G0 = -
RT ln
Kp, находим:
- 228596 = -19,14 - 298 lg Kp, отсюда lg Kp = 228596/(19,14 · 298) = 40,07 и Kp = рH2O (pH2p
) = 10
40,07.
Таким образом, если в исходной смеси парциальное давление каждого из трех газов составляло 1, то при равновесии парциальные давления водорода и кислорода будут исчезающе малы.
Если ΔG
- большая положительная величина, то константа равновесия очень мала и равновесие реакции сдвинуто в сторону исходных веществ. Так, для реакции окисления азота 1/2N
2г + 1/2O
2г = NO
г; Δ
G
= 87000 Дж/моль и, следовательно, в смеем, в которой
pN2 =
pO2 =
pNO = 1 будет происходить образование NO, а, наоборот, будет иметь место его диссоциация. В этом случае
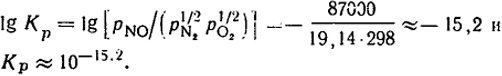
70
Таким образом, положительное значение ΔG
означает, что данное соединение неустойчиво при стандартных температуре и давлении и должно распадаться на составляющие его элементы.
Для реакций, в которых участвует больше чем одно соединение, способ расчета равновесия с помощью таблиц рассмотрим на примере реакции:
СОг + Н2ОГ = СО2Г + Н2Г.
Изменение энергии Гиббса при таких реакциях равно разности между суммой Δ
образования продуктов реакции и такой же суммой Δ
исходных веществ. Величины Δ
для СO
2, СО и Н
2О соответственно равны: -394383, -137268 и 228596 Дж/моль (для Н
2Δ
G
= 0). Отсюда для реакции Δ
= -28515 Дж/моль. Если, например, в исходной смеси газов парциальные давления равны атмосферному, то реакция пойдет слева направо до установления равновесия, при котором
lg Kp = lg[(pCO2pH2)/(pCOpH2O) = 28515/(19,14·298) и Кр ≈ 105.
Примером реакции, в которой равновесие не столь сильно смещено в одну сторону, является образование хлористого сульфурила: SO2г + Cl2r = SO2Cl2ж, где ΔG
для SO
2 составляет -300369, для SO
2Cl
2 - 313800 Дж/моль и, следовательно, для реакции Δ
G
= 13430 Дж/моль, откуда
Kp = 224.
Необходимо предостеречь от ошибочного вывода, заключающегося в том, что положительная величина ΔG0 означает полную невозможность протекания данной реакции в прямом направлении и получения технологически приемлемого выхода ее продуктов. Как уже отмечалось, величина ΔG0 характеризует равновесие лишь в случае, если все участники реакции имеют одинаковые парциальные давления, равные атмосферному. Если же изменить эти давления, то согласно уравнению (III.18) изменится и направление реакции. В газовых реакциях, где изменяется число молей газов, равновесие зависит и от общего давления. Как было показано выше, несмотря на очень малое значение Кp (и положительный знак ΔG0), в реакции синтеза аммиака достигается сравнительно высокий выход, благодаря использованию высоких давлений. Изменение константы равновесия с изменением температуры можно найти, подставляя в уравнение Гиббса-Гельмгольца (II.41) значение ΔG0/T = -RlnKp из уравнения изотермы:
d In Kp/dT = ΔH0/RT2
(III. 19)
Это важное соотношение, выражающее зависимость константы равновесия от температуры, называемое уравнением
71
изобары, было выведено Вант-Гоффом. Оно показывает, что знак производной dln
Kp/d
T определяется знаком изменения энтальпии реакции (теплового эффекта). Если эта производная положительна, то функция lп
Кp является возрастающей. Поэтому для эндотермических реакций, когда Δ
H0 положительно, константа равновесия увеличивается при возрастании температуры. Для экзотермических реакций (Δ
H0 отрицательно) константа равновесия уменьшается при увеличении температуры. В случаях очень малого (близкого к нулю) теплового эффекта реакции
Кp почти не зависит от температуры.
Если константа равновесия выражена через концентрации, то справедливо соотношение:
d ln Kc/dT = ΔU0/RT2,
(III.20)
называющееся уравнением изохоры химической реакции. Из уравнений (III.19) и (III.20) следует, что соединения, образующиеся с поглощением тепла, становятся более устойчивыми при высоких температурах, а экзотермические соединения более прочны при низких.
Здесь для качественного рассмотрения может быть использован упоминавшийся в предыдущем параграфе принцип Ле-Шателье. Например, повышение температуры равновесной смеси газов Н2, О2, Н2О приводит к увеличению диссоциации водяного пара, сопровождающейся поглощением тепла. Однако принцип Ле-Шателье не имеет общего характера. Он был предложен как аксиома, не опирающаяся на какой-либо определенный физический закон. Применение принципа Ле-Шателье в некоторых случаях может привести к ошибочным утверждениям.
Для того, чтобы проинтегрировать уравнение (III.19) или (III.20), примем сначала приближение, согласно которому энтальпия (внутренняя энергия) реакции не зависит от температуры. Оно может быть более или менее обоснованным, если изменение теплоемкости при реакции близко к нулю или рассматривается небольшой интервал температур. Тогда
lg Kp =
∫
d
T + 1,
или
lg Kp = -ΔH0/19,14T + I,
(III.21)
где I - постоянная интегрирования.
Для более точного выражения Кp следует учитывать зависимость ΔH0 от температуры.
72
Уравнение (III.21) показывает, что при указанном приближении между lg Kp и 1/Т существует линейная зависимость. Для реакции: Н2г + 1/2S2г = H2Sг такая зависимость представлена на рис. III.2, из которого видно, что экспериментальные точки для
lgKp = lg(pH2S/pH2p
)
удовлетворительно укладываются на прямую линию в координатах lgKp - 1/T. Следовательно, по величине тангенса угла наклона этой прямой линии может быть найдена
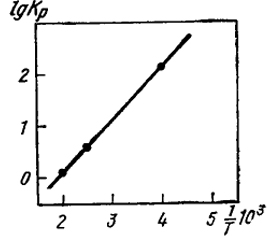
Рис. III.2. Зависимость логарифма константы равновесия
Kp от 1/
T для экзотермической реакции
энтальпия реакции, т.е. ΔH0 = tg α·19,14 = -1,05·103 × 19,14 = -20100 Дж/моль.
Рассмотрим пример приближенного расчета Кp для реакции:
СОг + Н2Oг = СО2Г + Н2Г.
Для подобных реакций, происходящих без изменения числа молей (Δn = 0), изменение теплоемкости также часто близко к нулю. Использование уравнения (III.21) позволяет, зная Кp при одной температуре и энтальпию реакции, найти константу равновесия при другой температуре Для рассматриваемой реакции при высоких температурах ΔH0 = -30540 Дж/моль, при 600 К Kp = 15,24. Найдем величину Кp при 1000 К. Для этого используется уравнение (III.21) в виде:
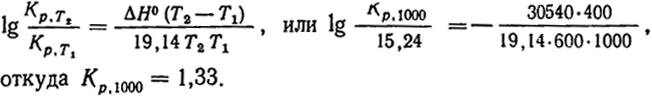
откуда Kp,1000 = 1,33.
Принятое приближение отвечает независимости изменения энтропии реакции от температуры. Действительно, умножая обе части уравнения (III.21) на (-RT) и переходя
73
к натуральным логарифмам, найдем ΔG0 = -RTlnKp = ΔH0 - T·RI.
Сопоставление этого уравнения с известным соотношением ΔG = ΔH - TΔS показывает, что ΔS0 = 2,303RI, т.е. ΔH0 не зависит от температуры. Это является следствием допущения ΔCp = 0, так как из уравнения (II.45) следует, что
(∂ΔS/∂Т)р = ∂Cp/T.
В таблицах стандартных величин приводятся значения энтальпий и энтропии соединений и простых веществ. В то время как величины энтальпий относительны (энтальпия простых веществ принимается равной нулю), значения энтропии в этих таблицах абсолютны (см. гл. IV).
Табличные данные для ΔH0 и S позволяют проводить расчеты равновесий в рамках описанного выше приближения.
В качестве примера вычислим выход NO (x) при окислении азота при 4000 К.
1/2N2г + 1/2O2г = NOг.
Общее давление равно 1 атм, а исходные числа молей N2 и О2 равны ?. Величина ΔH
для NO составляет 90400 Дж/моль (для N
2 и О
2 Δ
H
= 0). Величины
S
для 1/2 О
2, 1/2 N
2 и NO соответственно равны 191,5/2, 205,1/2 и 209,66 Дж/(моль·К). Отсюда
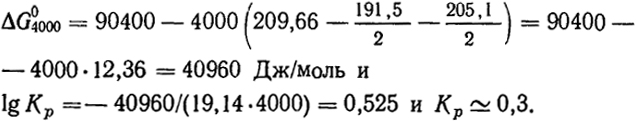
При равновесии парциальные давления N2H и O2 составят 1/2(1 - x) атм, а парциальное давление NO x атм, откуда
0,3 =
| x |
| [1/2(1 - x)]1/2[1/2(1 - x)]1/2 |
и x = 0,13, т.е. выход составляет лишь 13 %.
Точное решение уравнения (III.21) требует знания зависимости величины ΔH0 реакции от температуры. Кроме того, необходимо знать значение постоянной I. Рассмотрим такое решение для реакции синтеза аммиака: 3H2г + N2г = 2NH3г, для которого ΔH
= -92380 Дж, а теплоемкости участвующих в ней веществ составляют:
Cp,H2 = 27,2 + 3,76·10-3T;
74
CpN2 = 27,2 + 4,18·10-3T;
Cp,NH3 = 33,64 + 2,93·10-3T + 2,09·10-5T2.
Отсюда
ΔCp = 2Cp,NH3 - 3Сp,H2 - Cp,N2 = -41,5 - 9,62̭10-3T + 4,18·10-5T2.
Подставляя это выражение в уравнение (I.29) и интегрируя от 0 до 298 К, получим:
- 92380 = ΔH
- 41,5·298 - 4,81·298 + 1,38·10
-5·298
3,
откуда ΔH
= -79500 Дж/моль и общее выражение для энтальпии реакции как функции температуры имеет вид:
ΔH
= -79500 - 41,5
T - 4,81·10
-3 Т2 + 1,38·10
-5T3.
При подстановке этого выражения в уравнение (III.21) и интегрировании найдем:
lg Kp =
-
lg
T -
+
T2 +
I.
Для того чтобы найти значение постоянной интегрирования I, необходимо экспериментально определить величину Кp хотя бы при одной температуре.
Из опытов Габера известно, что, например, при 673 К lg Kp = -3,74. Используя это значение, находим, что I = 4,2. После упрощения получаем:
lg Kр = (4154/T) - 4,99 lg Т - 0,25·10-3 T + 0,36·10-6 T2 + 4,2.
Естественно, что это уравнение справедливо лишь в том интервале температур, в котором соблюдаются использованные уравнения для теплоемкостей. Из приведенного примера видно, что для нахождения константы равновесия при определенной температуре и соответственно выхода реакции необходимы следующие опытные данные: уравнения для температурной зависимости теплоемкостей участвующих в реакции веществ в рассматриваемой области температур; величина изменения энтальпии (тепловой эффект) реакции при какой-либо температуре в этой области и хотя бы одно значение константы равновесия.
75
