Процессы, заключающиеся в превращении одной фазы данного вещества в другую фазу того же вещества и, следовательно, протекающие без химических реакций, называются фазовыми превращениями (плавление, возгонка, полиморфные превращения).
Основной характеристикой фазового превращения является температура, при которой фазы находятся в равновесии. Эта температура зависит от давления. Так, температура плавления льда или, например, температура перехода α-железа в γ-железо меняются в зависимости от давления. При данной температуре давление насыщенного пара (в равновесии с жидкостью) имеет вполне определенное значение. Состояние равновесия определяется связью между равновесной температурой и равновесным давлением.
Для нахождения этой связи учтем, что при сосуществовании двух фаз (1 и 2) одного и того же вещества при постоянных р и Т их молярные энергии Гиббса G1 и G2 равны. Поэтому условием равновесия между двумя фазами при малых изменениях р и Т является равенство dG1 = dG2. Согласно уравнению (II.32)
V1dp + S1dT = V2dp - S2dT,
где V1 и V2 - молярные объемы;
S1 и S2 - молярные энтропии. Отсюда следует, что
=
=
,
55
где ΔV и ΔS - изменения объема и энтропии при изотермическом фазовом превращении одного моля вещества.
Хотя при фазовом превращении объем изменяется, давление остается постоянным. Например, при испарении жидкости, происходящем при постоянной температуре, давление пара не изменяется. Поэтому производная в левой части последнего уравнения является полной.
Так как процесс фазового превращения является изотермическим и равновесным, то ΔS = Q/T и
dp/dT = Q/TΔV,
(III.1)
где Q - тепло, придаваемое системе при превращении.
Для равновесия жидкость - пар уравнение (III.1) дает зависимость упругости насыщенного пара от температуры, а также температуры кипения от давления. Поскольку V2п больше V1Ж и при превращении жидкости в пар придается тепло Q, то производная dp/dT положительна и, следовательно, с повышением температуры давление пара должно увеличиваться. Величина Q здесь равна ΔHисп, часто обозначаемой λ.
Такие же следствия из уравнения (III.1) можно получить для равновесия твердое тело-пар, где Q соответствует энтальпии сублимации ΔHсуб(σ).
Для равновесия в системе твердая фаза (1) - жидкость (2) уравнение (III.1) дает зависимость температуры плавления от давления:
dT/dp = T(V2 - V1)/Q.
При переходе 1 → 2 тепло придается системе, и Q (энтальпия плавления ΔHпл) положительна (ΔHпл обозначают и буквой ρ). Следовательно, знак производной зависит от разности объемов твердой и жидкой фаз. Если при плавлении объем увеличивается (V2 > V1), то с ростом давления температура плавления будет повышаться. Если же V2 < V1, то с повышением давления температура плавления должна уменьшаться.
У большинства веществ разность (V2 - V1) положительна. Исключение составляют Н2О, Bi, Ga и некоторые марки чугуна. При превращении лед - жидкая вода объем уменьшается (ΔV - отрицательная величина), поэтому температура плавления льда понижается при увеличении давления (на 0,007° C при росте давления на 1 ат).
Применение уравнения (III.1) для аллотропических превращений можно иллюстрировать на примере превращения железа из α- в γ-модификацию, которое при атмосферном
56
давлении происходит при 910° C. Это превращение сопровождается поглощением тепла (900 Дж/моль). Плотность α-Fe составляет 7,571 г/см3, а γ-Fe 7,633 г/см3. Чтобы получить размерность величины dT/dp в градусах на атмосферу или на 105 Па, следует теплоту процесса выразить в л·Па·105, а изменение объема при превращении в л. Учитывая, что 1 Дж эквивалентен 9,8·10-3 л·Па·105, для одного моля атомов. Fe
ΔV = 55,85(
-
) = -0,06 см
3 = -0,06/1000 л.
= -
| (910 + 273)·0,06 |
| 900·9,8·10-3·1000 |
= -0,0080 K/10
5 Па,
т.е. при увеличении давления на одну атмосферу (105 Па) температура превращения α-γ уменьшается на 0,0080 К. Следует, однако, иметь в виду, что приведенный расчет носит упрощенный характер, так как в нем не принимается во внимание зависимость теплоты превращения от температуры, а температура берется постоянной. Поэтому он дает точные результаты лишь при сравнительно небольших изменениях давления.
Уравнение (III.1) было найдено Клапейроном еще до открытия первого закона термодинамики и затем выведено Клаузиусом и носит название уравнения Клапейрона-Клаузиуса. Это уравнение позволяет найти важную для практики зависимость давления насыщенного пара жидкости или твердого тела от температуры. Для первого случая
=
.
Если Т значительно ниже критической, то величиной объема жидкости можно пренебречь по сравнению с величиной объема пара. Кроме того, при условии, что пар ведет себя как идеальный газ Vп = RT/p, откуда (1/р)(dp/aT) = = ΔHисп/RT2 или
d ln p/dT = ΔHисп/RT2,
(III.2)1
и, наконец,
ln p = ∫
dT + C,
(III.3)
где С - постоянная.
57
Очевидно, для давления насыщенного пара твердого тела уравнение (III.2) имеет вид: d ln p/dT = ΔHcyб/RT2, где ΔHсуб - энтальпия сублимации (σ).
Заменяя натуральный логарифм в уравнении (III.3) десятичным, получим:
lgp = 1/19,14 ∫
+ i.
(III.4)*
Постоянная интегрирования I называется химической постоянной. Для нахождения упругости пара необходимо знание величины i и зависимости ΔHисп от температуры. Как и для любого теплового эффекта, температурная зависимость теплоты испарения описывается уравнением. Кирхгофа:
dΔHисп/dT = Срп - Срж,
(III.5)
которое, как отмечалось, не совсем точно.
В качестве первого приближения примем, что теплоемкости пара и жидкости равны. В этом случае ΔHисп не зависит от температуры, и из уравнения (III.4) следует, что
lgp = -ΔHисп/19,14T + i.
(III.6)
Естественно, что вследствие принятого допущения это уравнение грубо приближенно и может дать удовлетворительную точность лишь при использовании в небольшом интервале температур, в котором величина ΔHисп практически постоянна. В этом случае для получения зависимости р от Т необходимо знать две величины: ΔHисп и i
Уравнение (III.6) часто используют в качестве интерполяционного в следующей форме: lgp = (A/T) + B, где А и В - постоянные. В некоторых случаях подобные уравнения дают удовлетворительную точность в относительно большом интервале температур. Так, например, давление пара жидкого алюминия при 1290 К составляет 10-11 Па, а при 1545·10-7 Па.
Требуется найти давление пара, например, при 1405 К. Найдем сначала значения А и В из двух уравнений для 1290 и 1545 К:
- 11 = (A/1290) + В и -7 = (A/1545) + В;
A = -15636 и В = 6,118.
Отсюда искомая величина lgp =
+ 6,118 = -5,008, т.е.
р ≈ 10
-5 Па.
58
Другой способ приближенного вычисления давления пара требует знания энтальпии испарения и температуры кипения данного вещества. Так, для алюминия энтальпия испарения составляет 299156 Дж/моль, а температура кипения 2600 К. При температуре кипения давление насыщенного пара над жидкостью достигает внешнего атмосферного и равно единице. Подставляя эти значения в уравнение (III.6), найдем:
0 = -
+
i, т.е.
i = 6,01.
Отсюда для температуры 1405 К
lgp = -
+ 6,01 = -5,11.
Небольшое отличие от полученного выше результата объясняется тем, что во втором случае интерполяция проводилась в более широком интервале температур.
В тех случаях, когда отсутствуют данные о теплотах испарения жидкостей, для приближенной оценки этой величины может быть использовано эмпирическое правило Трутона. Согласно этому правилу, для многих жидкостей отношение теплоты испарения к абсолютной температуре кипения есть величина постоянная, близкая к 22, т. е. ΔHисп/Tкип = 221.
Правило Трутона удовлетворительно выполняется для неассоциированных жидкостей. Теоретически более обосновано правило Гильдебрандта, согласно которому для жидкостей отношения теплоты испарения к абсолютной температуре одинаковы при температурах, при которых одинаковы концентрации паров.
Для оценки давления пара может быть использовано эмпирическое правило Дюринга, устанавливающее, что отношение абсолютных температур, при которых давление паров двух подобных веществ одинаково, есть величина постоянная. Так, например, температуры кипения железа и марганца соответственно равны 3008 и 2370 К и их отношение 3008/2370 = 1,27. Зная, что при 2277 К давление пара железа равно 103 Па, можно найти температуру (2277/1,27 = 1792 К), при которой давление пара марганца будет иметь такое же значение, что сравнительно близко к наблюдаемой величине (1750 К).
Для более строгого решения задачи о зависимости давления
59
пара от температуры следует учитывать, что теплоемкости конденсированной фазы (жидкой или твердой) и пара неодинаковы и зависят от температуры, т.е. dΔHисп/dT = Ср(п) - Ср(конд), или в интегрированной форме:
ΔHисп = ΔH0 +
[
Ср(п) -
Ср(конд)]d
T,
где ΔH0 - постоянная.
Подставляя это выражение в уравнение (III.4), получим:
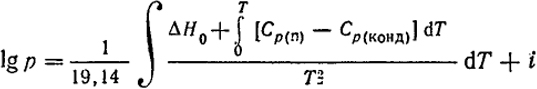 (III.7)
(III.7)
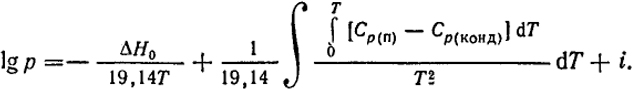 (III.8)
(III.8)
Таким образом, чтобы найти уравнение, связывающее давление пара и температуру в каком-либо интервале температур, необходимо знать теплоемкости пара и конденсированной фазы в зависимости от температуры в этом интервале, теплоту испарения и давление пара при одной температуре. В качестве второго приближения при решении этой задачи принимается, что теплоемкости не зависят от температуры, тогда из уравнения (III.8) следует:
lgp =
+
lgT + i
(III.9)
Для решения ряда задач важно определить энтальпию (теплоту) испарения и сублимации. Для веществ, у которых эти превращения происходят при высоких температурах, например, для металлов, особенно тугоплавких, калориметрические измерения ΔHисп и ΔHсуб весьма трудны. В этих случаях указанные величины находят из измерений давления пара при разных температурах.
Уравнение (III.2) может быть переписано в виде:
= -Δ
Hисп/
R,
откуда следует, что графически величины ΔHисп или ΔHсуб
60
могут быть найдены из значения тангенса угла наклона касательной к линии, построенной в координатах ln p - (l/T). Если эта линия кривая, то полученное значение ΔHисп относится к температуре, соответствующей точке касания. На рис. III.1 представлена зависимость логарифма парциального давления жидкого железа от l/T.
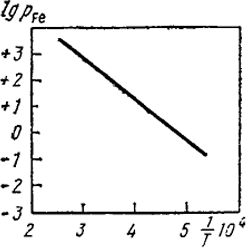
Puc. III.1. Зависимость логарифма давления насыщенного пара железа от обратной абсолютной температуры
61
1
Множитель 19,14 есть произведение универсальной газовой постоянной
R = 8,314 Дж/моль и коэффициента перехода от натуральных логарифмов к десятичным, равного 2,303.
1
Здесь Δ
Hисп следует выражать в кал.
