Макроскопические свойства тел сводятся к макроскопическим характеристикам атомных образований, из которых они состоят. В гл. XIII мы видели, что термодинамические свойства газов могут быть определены из значений постоянных, характеризующих свойства молекул (моменты инерции, частоты колебаний и т.п.).
Возникает задача экспериментального определения характеристик молекул, которые в основном могут быть разбиты на четыре группы: 1) геометрические; 2) динамические; 3) энергетические и 4) диэлектрические.
Геометрические характеристики определяются формой и размерами молекул.
Динамические характеристики передают силы, возвращающие атомы в исходное состояние, и, следовательно, частоты колебаний, связанные с этими силами.
К энергетическим характеристикам относятся энергия образования молекул, энергии отдельных связей и пр.
661
Диэлектрические характеристики включают прежде всего дипольный момент и поляризуемость.
Среди физических методов исследования молекул особую роль играет изучение молекулярных спектров. Молекулярные спектры называют полосатыми, так как они достоят не из линий (как атомные спектры), а из обладающих сложной структурой полос.
Сложность молекулярных спектров определяется тем, что энергия молекул складывается из электронной, колебательной и вращательной.
Квант поглощаемой (или испускаемой) лучистой энергии определяется, вообще говоря, изменением этих видов энергии. Изменение только вращательной энергии (при постоянной колебательной и электронной) имеет место в так называемом вращательном или ротационном спектре молекул. Вследствие того, что величина кванта вращения мала, вращательные спектры лежат в инфракрасной части спектра. Так как испускание или поглощение света возможно лишь в случае периодического изменения дипольного момента, то вращательные спектры имеют лишь полярные молекулы.
В гл. XXII было показано, что энергия вращения определяется уравнением ε = (h28π2I)l(l + 1).
Правило отбора для вращательного квантового числа запишется следующим образом: Δl = ±1, поэтому частота поглощаемого (или испускаемого) света определится соотношением
ν =
[
El -
El - 1] =
[
l(
l + 1) -
l(
l - 1)] =
l.
Следовательно, вращательный спектр представляет собой группу линий, находящихся на одинаковом друг от друга расстоянии (равном h/4π2I).
Измеряя это расстояние, можно определить момент инерции, следовательно, расстояние между атомами. Из вращательных спектров многоатомных молекул определяются все три момента инерции.
Как было показано в гл. XXII, полная собственная функция в соответствии с принципом Паули, должна быть антисимметрична в отношении обмена одинаковых частиц. Поэтому полная функция, описывающая вращение симметричных молекул, должна быть антисимметрична.
Координатная часть полной собственной функции вращения является четной (содержит четные степени cosθ) для четных значений l и нечетной для нечетных. При обменене
662
местами ядер угол θ меняется на 180° и cosθ изменяет знак. Следовательно, координатная часть полной функции симметрична в отношении обмена ядер для четных значений l. Из требований антисимметричности полной функции вытекает, что спиновая часть функции должна быть антисимметричной.
Таким образом, спины ядер молекул должны быть антипараллельны для четных значений l и параллельны для нечетных.
Можно показать, что самопроизвольные переходы могут быть только между состояниями, отвечающими четным (или нечетным) значениям l. Поэтому можно говорить о совокупности молекул с четными значениями как об одной модификации симметричной двухатомной молекулы (с отличным от нуля спином ядер), с нечетными - как о другой. Первая модификация называется парамолекулой, вторая - ортомолекулой. Так, существуют ортомолекулы и парамолекулы водорода.
При очень высоких температурах равновесное соотношение концентраций этих двух модификаций должно равняться 1/3, так как статистический вес значения спина, равного единице, в три раза больше значения, равного нулю (см. гл. XXIII.)
При очень низкой температуре должно быть представлено состояние с самой низкой энергией. В этом состоянии l = 0. Так как этот терм относится к парамодификации, то при снижении температуры равновесие должно сдвигаться от орто- к парамодификации.
Так как энергетические состояния у орто- и парамолекул различны, то вращательные теплоемкости модификаций и связанные с теплоемкостью свойства (например, теплопроводность) должны быть различны. Ввиду того, что вырождение вращательной теплоемкости доступно для наблюдения у водорода (см. гл. XIII), то впервые орто- и парамодификации были обнаружены у водорода.
Дипольные молекулы имеют и колебательные спектры, лежащие в коротковолновой части инфракрасных спектров.
Как указывалось (см. гл. XIII), двухатомная молекула представляет собой один осциллятор, а r-атомная эквивалентна 3r-6 осцилляторов.
Энергия гармонического осциллятора выражается следующим образом (см. гл. XXII): En = hν (n + 1/2), где ν - частота осциллятора.
Соответственно правилу отбора Δn = ±1. Для частоты
663
излучения получим
νиз =
= ν.
Таким образом, спектр двухатомной молекулы в случае гармонического колебания будет представлен линией, а многоатомной молекулы - 3r - 6 линиями.
Наложение изменения вращательной энергии должно превратить эти линии в полосы, состоящие из равноотстоящих линий. Однако реальные молекулы не могут быть гармоническими осцилляторами, так как в противном случае их потенциальная энергия как функция расстояния описывалась бы параболой и энергия диссоциации была бы бесконечно велика. В случае гармонического осциллятора расстояние между уровнями колебательной энергии одинаково (и равно hν). В реальной молекуле расстояние между уровнями должно понижаться по мере повышения энергии, образуя континуум для энергий, превышающих энергию диссоциации.
Для определения колебательных термов и частот колебательных спектров необходимо решить уравнение Шредингера для потенциальной энергии, описывающей взаимодействие атомов в молекуле как функцию расстояния.
Точная функция, передающая потенциальную кривую молекулы, очень сложна. Предложен ряд уравнений, приближенно ее передающих. Одной из наиболее простых является так называемая функция Морзе:
U(ρ) = D[(1 - eaρ)2 - 1],
(XXV.1)
где U - энергия молекулы, если расстояние между атомами равно R, а за нуль принимается энергия атомов:
ρ = (R - R0)/R0,
где R0 - расстояние, отвечающее минимуму энергии молекулы; D - энергия диссоциации молекулы; а - постоянная, смысл которой можно уяснить, рассмотрев величину энергии при малых значениях ρ.
Из уравнения (XXV.1) для малых ρ следует
U(ρ) = D(a2ρ2 - 1).
Для малых расстояний потенциальная кривая описывается параболой, соответствующей гармоническим колебаниям.
664
Из уравнения для гармонического осциллятора
U = k(R - R0)2/2
следует, что упругая постоянная k определяется через D и а:
k = 2Da2/R
,
а частота этого гармонического осциллятора ν
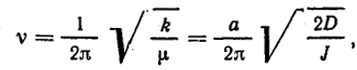
где J = μR
.
Таким образом, постоянная а непосредственно связана с частотой колебания.
Если выражение (XXV.1) подставить в уравнение Шредингера вместо U, то для энергии получим
E = hν[(n + 1/2) - x(n + 1/2)2];
(XXV.2)
х называется постоянной ангармоничности, т.е.
x = hν/4D.
Для малых значений п уравнение (XXV.2) переходит в уравнение для гармонического осциллятора.
Расстояние между соседними термами, согласно уравнению (XXV.2), убывает с увеличением п:
ΔE = hν[1 - 2x(n + 1)].
(XXV.3)
При n = (1/2x) - 1 расстояние между уровнями равняется нулю. Это происходит в точке, где колебательная энергия равна энергии диссоциации.
В соответствии с уравнением (XXV.3) частоты излучения, определяемые уравнением ν = ΔE/h, также должны уменьшаться с увеличением п.
Таким образом, колебательный спектр реальной двухатомной молекулы представляет собой серию полос, структура которых определяется изменением вращательной энергии. Из колебательных спектров определяется частота колебания молекулы и в принципе может быть определена энергия диссоциации, поскольку от ее величины зависят постоянная ангармоничности и уменьшение ΔE с п. Однако точность такого определения невелика. Энергия диссоциации определяется из электронных спектров молекул. Электронные спектры отражают одновременное изменение всех видов энергии молекул (электронной, бательной
665
и вращательной). Этот спектр дают все молекулы независимо от наличия дипольного момента. Одному электронному переходу отвечает в спектре целая система полос, перенесенная из инфракрасной части спектра, где она наблюдалась в случае колебательно-вращательного спектра, в ультрафиолетовую или видимую часть. При этом характеристики, определяющие колебательную и вращательную энергию (ν и J), в молекуле с возбужденным электроном и в молекуле, находящейся в основном состоянии, различны. Распределение интенсивности в системе полос определяется следующими обстоятельствами. При переходе электрона на более высокий уровень расстояние между ядрами не изменяется (принцип Франка-Кондона).
На рис. XXV.1 указаны две потенциальные кривые. Нижняя отвечает основному терму молекулы, а верхняя - терму возбужденной молекулы.
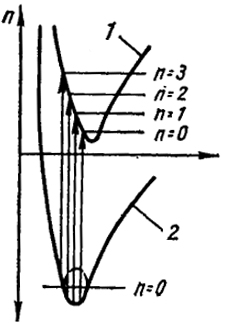
Рис. XXV.1. К вероятности переходов:
1 - возбужденное состояние:
2 - основное состояние
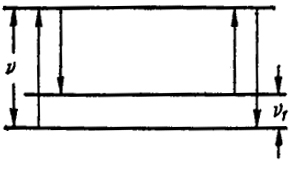
Рис. XXV.2. Схема эффекта комбинационного рассеяния
Мы видим, что равновесное расстояние для возбужденной молекулы (как это обычно и бывает) больше, чем для основного состояния. В последнем показан лишь самый нижний колебательный уровень (n = 0), для возбужденной - первые четыре колебательных уровня.
Собственная функция, определяющая вероятность различных
666
расстояний для основного состояния осциллятора, представляет собой гауссовскую кривую (см. гл. XXII). Эта кривая изображена на рис. XXV.1 пунктиром. Мы видим, что вертикаль, идущая от точки с наибольшей вероятностью (максимум кривой), пересекает потенциальную кривую возбужденной молекулы вблизи второго колебательного состояния.
Таким образом, для рассматриваемой молекулы возбужденная молекула окажется возбужденной по отношению не только к электрону, но и колебательной энергии. Вероятность перехода к другим колебательным уровням (также показанным на рис. XXV. 1) будет меньше. Если равновесное расстояние у возбужденной молекулы значительно больше, чем у молекулы в основном состоянии, то колебательная энергия у возбужденной молекулы может быть больше ее энергии диссоциации. Возникшая в результате электронного перехода возбужденная молекула должна диссоциировать, так как она рождается сильно сжатой. При этой фотодиссоциации избыток энергии переходит в кинетическую энергию атомов - продуктов диссоциации. Так как эта кинетическая энергия не квантуется, то фотодиссоциации отвечает сплошной участок спектра.
В зависимости от колебательного уровня и расстояний между ядрами в молекулах в возбужденном и основном состояниях при электронном переходе может произойти фотодиссоциация либо переход возбужденной молекулы обратно; в основное состояние. Такой спектр будет состоять из дискретной (полосатой) и сплошной частей, как это наблюдается в ряде случаев (Cl2, Br2, I2, O2 и др.).
По границе между этими частями спектра можно определить энергию диссоциации молекул.
Таким образом, молекулярные спектры позволяют определить геометрические, динамические и энергетические характеристики молекул. При этом для дипольных молекул первые две группы могут быть определены из находящихся в инфракрасной части спектра вращательно-колебательного спектров.
Простой метод определения характеристик молекулы дает изучение так называемого спектра комбинационного рассеяния, открытого независимо в СССР Л.И. Мандельштамом и Г.С. Ландсбергом для твердых тел и в Индии В. Раманом для жидких.
Эффект комбинационного рассеяния заключается в том, что в рассеянном каким-либо телом свете, которым
667
тело облучалось с частотой v, наблюдаются измененные частоты, симметрично расположенные относительно основной.
Квантовая теория эффекта комбинационного рассеяния очень проста. Как показано на рис. XXV.2, возбужденная в результате облучения молекула может вернуться не на основной уровень, а на возбужденный (например, в отношении колебательной энергии). При этом, как видно из левых стрелок рис. XXV.2, частота испускаемого света меньше частоты рассеиваемого. Если в момент облучения молекула была в возбужденном состоянии, то, как показывают правые две стрелки (см. рис. XXV.2), частоты испускаемого света больше частоты первоначального.
В первом случае испускается частота ν - ν1, а во втором ν + ν1, где ν - частота излучения, которым тело облучается, a ν1 - частота, возникающая при переходе молекулы из основного терма в один из вышележащих (см. рис. XXV.2).
Линии с измененной частотой называют спутниками. Естественно, что интенсивность спутника с повышенной частотой должна быть меньше, чем интенсивность спутника с пониженной, так как первый вид излучения требует наличия возбужденных молекул. С ростом температуры интенсивность этой линии ν + ν растет.
Следовательно, изучение спектра комбинационного рассеяния позволяет изучать спектр тела, который переносится таким образом в другую часть спектра. Обычно тело облучается светом ртутной лампы. Изучение рассеянного света позволяет исследовать, например, чистый колебательно-вращательный спектр, который, как указывалось, лежит в инфракрасной части спектра, изучение которой представляет ряд экспериментальных трудностей.
Отметим, что эффект комбинационного рассеяния проявляется особенно у недипольных молекул, для которых
Таблица XXV.1. Характеристики двухатомных молекул

668
Таблица XXV.2. Характеристические частоты некоторых атомных групп

чистые колебательно-вращательные спектры вообще отсутствуют.
В табл. XXV.1 собраны некоторые результаты измерения характеристик молекул различными методами.
Постоянство значений некоторых характеристик связей позволяет использовать их для определения структуры химических соединений, качественного и количественного анализов. В табл. XXV.2 даны значения характеристических частот некоторых групп атомов.
669
