§ 4. Сплавы

Термодинамические свойства сплавов должны зависеть от геометрических факторов (размера радиусов атомов) и характеристик электронов. Для образования двумя металлами непрерывного ряда твердых растворов необходимо, чтобы они имели одинаковую кристаллическую решетку. Так, при температуре выше 910° C железа имеет общую с никелем гранецентрированную кубическую решетку, и в интервале 910-1460° C никель и железо образуют непрерывный ряд твердых растворов. Ниже 910° C железо имеет объемноцентрированную решетку, в то время как никель сохраняет гранецентрированную, поэтому при 600° C в объемноцентрированной решетке железа растворяется лишь 7 % никеля. Растворы железа в никеле имеют гранецентрированную решетку.

Юм-Розери пришел на основе рассмотрения большого экспериментального материала к выводу, что для. образования непрерывного ряда твердых растворов радиусы атомов должны отличаться не больше чем на 15 %.

В качестве примера сплава, удовлетворяющего всем этим требованиям, можно назвать непрерывный ряд растворов золота и серебра, радиусы атомов которых отличаются на 2 %. Радиус атома меди на 13 % меньше, чем атомов золота и серебра. С золотом медь образует непрерывный ряд сплавов, в то время как серебро в меди почти нерастворимо. Это говорит о недостаточности одних геометрических требований.

Так как электроны всех компонентов раствора входят в общий электронный газ, то валентность отдельных атомов утрачивает свое значение. Свойства решетки должны зависеть от среднего числа электронов, приходящихся на один атом. Эту величину называют электронной концентрацией.

Как в атомных решетках структура решетки определяется валентностью (правило 8 - N), так и в металлах кристаллическая структура должна зависеть от величины электронной концентрации.

Рассмотрим типичную диаграмму состояний Cu-Zn (рис. XXIV.7). Аналогичные диаграммы дает медь также со следующими элементами: Ag, Cd, Al, In, Sn. Подобные диаграммы образуют и многие другие бинарные сплавы [например, Ag-Zn, Ag-Sn и др. (рис. XXIV.8)].

Во всех случаях α-фаза (см. рис. XXIV.7) имеет гранецентрированную кубическую решетку, ε-фаза - гексагональную

649

плотноупакованную, ρ - кубическую объемно-центрированную, а γ - сложную кубическую (так называемую гигантскую кубическую).

Переходы из одной решетки в другую происходят при разных атомных концентрациях (одинаковом числе валентных электронов на один атом). Так, решетки типа

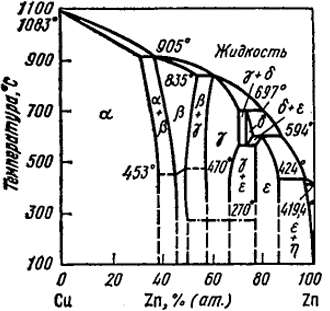
Рис. XXIV.7. Диаграмма состояния Cu-Zn

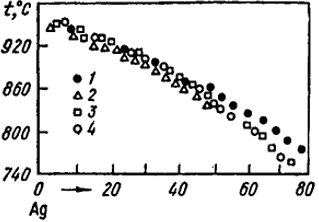
Рис. XXIV.8. Кривые ликвидус растворов различных веществ в серебре:
1 - Cd; 2 - In; 3 - Sn; 4 - Sb

β-латуни (объемноцентрированная кубическая) образуются в разных бинарных сплавах при возникновении соотношений между компонентами, выражаемых формулами: CuZn, CuBi, AgZn, AgCd, AuCd, AuZn, Cu₃Al, Cu₃Ge, Cu₃Zn, CoAl, NiAl и FeAl.

Если принять валентность Си, Ag и Аu равной единице; Be, Zn, Cd - двум единицам; А1 - трем; переходных элементов- нулю, то во всех этих случаях на каждый атом придется по 1,5 электрона.

Точно так же решетка γ-латуни возникает, когда электронная концентрация равна 1,61 (например, Cu₅Zn₈, Сu₃А1₄ и т.д.). При достижении электронной концентрацией значения 1,75 (например, CuZn₃, Ag₃Sn, AusAl₃ и т.д.) возникает гексагональная плотноупакованная решетка.

Джонс объяснил эти закономерности особенностями образования зон Бриллюэна. Сфера Ферми (т.е. значение максимальной энергии) приходит в соприкосновение с границей зоны Бриллюэна при определенном значении электронной концентрации. Дальнейшее изменение концентрации

650

компонента с большей валентностью должно вызвать заполнение следующей зоны, поэтому решетка делается термодинамически менее выгодной, чем другая с незаполненной зоной.

При таком объяснении предполагается, что изменения остальных факторов, от которых зависит энергия решетки, меньше, чем изменения энергии электронов вследствие начала заполнения следующей зоны, поэтому такого рода правила имеют обычно исключения. Например, если считать, что электронная концентрация определяет структуру решетки, то все металлы одной группы менделеевской таблицы должны иметь одинаковую структуру. Действительно, Li, Na, К, Rb и Cs кристаллизуются в объемно-центрированной кубической решетке, но Са и Sr в гране-центрированной, в то время как Ва - в объемноцентрированной.

Естественно ожидать, что от величины электронной концентрации должны зависеть также термодинамические свойства -твердых и жидких сплавов. Действительно, Юм-Розери показал, что кривые ликвидуса и солидуса для растворов различных элементов в одном растворителе совпадают, если вместо атомных процентов на оси абсцисс откладывать электронные (процент электронов, внесенный в общий электронный газ атомами растворителя). Рис. XXIV.8 иллюстрирует эту закономерность на примере кривой ликвидуса для растворов различных веществ в серебре.

Мы рассматривали растворы двух металлов. Положение существенно изменяется, если один из компонентов в чистом виде является металлом, а другой образует атомную решетку. В этом случае растворы в сколько-нибудь широком интервале концентраций не образуются, даже если атомы компонентов имеют близкие радиусы. Промежуточные фазы также существуют в узкой области концентраций.

Все сказанное относилось к растворам замещения. Обычно карбиды, бориды, нитриды и гидриды имеют металлический характер, если образуются переходными металлами. Структура этих соединений в значительной степени определяется геометрическим фактором. Согласно правилу Хэгга, если отношение радиуса атома неметалла к радиусу атома металла меньше 0,59, то атомы металла образуют простую решетку (обычно гранецентрированный куб или плотную гексагональную, а в некоторых случаях объемноцентрированную кубическую или простую гексагональную).

651

Если рассматриваемое отношение больше 0,59, то образуется более сложная структура. Г. Хэгг обосновал критическую величину отношения радиусов, рассматривая условия упаковки атомов неметаллов в тетраэдрических порах решетки металла.

Многие из указанных выше методов рассмотрения металлической связи могут применяться для описания энергии образования сплавов.

Эта задача осложняется прежде всего тем, что при образовании сплавов существенную роль играет химическое взаимодействие между компонентами. Так, различная электроотрицательность должна приводить к переходу электрона от атома одного элемента к атому другого, т.е. к возникновению явления, подобного гетерополярной связи. При этом большое значение имеет характер заполнения электронных состояний атомов. Атомы с недостроенными оболочками должны проявлять акцепторные свойства. Действительно, тенденция к образованию интерметаллидов, проявляющаяся в элементах с недостроенными оболочками, резко уменьшается у меди, d-оболочка которой заполнена.

При применении метода Вигнера и Зейтца для расчета энергии сплава следует учесть энергию упругой деформации решеток, компонентов от их собственного объема до среднего объема в сплаве, а также необходимость выравнивания электронной плотности на границах ячеек Вигнера - Зейтца.

На основе подобного рассмотрения Миедама предложил полуэмпирическую формулу для энергии образования сплава (ΔU) металлов с недостроенными d-оболочками:

ΔU = φP[-(ΔΦ)² + Q(Δn)^1/3],

где φ - функция, зависящая от состава сплава; ΔΦ - разница электроотрицательности, которую оценивают по работам выхода электронов; n - электронная плотность на границах атомных ячеек; Р, Q - постоянные.

Правильнее рассматривать не заполнение электронных состояний атомов, а электронных зон. В ряде работ показано, что энергия образования сплава переходных элементов определяется в первую очередь d-зоной, ее смещением при образовании сплава и ее деформацией. Эти характеристики существенно зависят от положения компонентов в таблице Менделеева и прежде всего от заполненности d-оболочек.

652