Энергия металлической решетки (U) может быть получена из опытных данных на основе закона Гесса следующим образом. Разделение решетки на элементы, т.е. на ионы и электроны, можно представить себе в виде двух последовательных процессов: сублимации металла и ионизации атомов. Таким образом, U = -σ - V, где σ - теплота сублимации решетки; V - потенциал ионизации атома.
Теоретический расчет величины U представляет собой весьма непростую задачу. Одно из основных отличий энергии металлической решетки от ионной заключается в наличии кинетической энергии у электронов (Ек). Нулевая энергия колебания ионов решетки вносит малый вклад в ее энергию. Нулевая энергия электронов благодаря их малой массе определяет наряду с их потенциальной энергией энергию металлической решетки.
Мы уже рассматривали ранее (см. гл. XIV и XXII) простейшую модель металла, в которой каждый электрон движется независимо от других в некотором потенциальном поле, созданном всеми положительными ионами и остальными электронами. В простейшем приближении этот потенциал описывается моделью потенциального ящика, т.е. принимается постоянным внутри металла.
Мы видели, что решение уравнения Шредингера приводит к ряду дискретных уровней энергий, расстояние между которыми падает с увеличением размера потенциального ящика. Поэтому для металла достаточно большого объема можно считать, что спектр энергии электронов сколь угодно близок к непрерывному. Согласно принципу Паули, на каждом уровне могут находиться два электрона с противоположными спинами.
637
Таким образом, при абсолютном нуле должны быть заполнены все уровни, находящиеся ниже некоторого критического. Это обстоятельство и принцип Паули объясняют явление вырождения электронов (см. гл. XIII).
В классической теории теплоемкости металлов отсутствует член, отвечающий теплоемкости электронов, не потому, что квант энергии электрона велик. Дело в том, что при повышении температуры увеличить энергию могут лишь электроны металла, находящиеся на самом высоком уровне. Остальные электроны не могут подняться на более высокие уровни, так как эти уровни уже заняты другими электронами.
В самой простой и крайне грубой модели металла расчет энергии металлической решетки проводится на основе учета кинетической энергии электронов по формуле, выведенной ранее с помощью статистики Ферми. Потенциальная энергия при этом рассчитывалась на основе учета электростатического взаимодействия положительных ионов с равномерно распределенными электронами. Таким образом, расчет как кинетической, так и потенциальной энергии, проводится в приближении постоянного потенциала поля, в котором двигаются внутри металла электроны.
На самом деле электроны двигаются в периодическом поле, так как около каждого положительного иона существует потенциальная яма. Поэтому собственная функция электронов должна отражать как движение между положительными ионами, так и вокруг ионов. Если расстояния между ионами стремятся к бесконечности, то электроны сядут на свои орбиты около положительных ионов. Существует грубая аналогия между движением электрона в металле и колесом. Электрон и движется поступательно и вращается вокруг ионов. Поступательное движение мы описали методом постоянного потенциала (картины плоских волн).
Можно показать (теорема Блоха), что для движения одного электрона в периодическом поле собственная функция имеет следующий вид для движения по одной оси: ψ = exp (ikx)Uk(x).
Первый множитель описывает волну, а второй обладает периодичностью поля. Разделяют случаи сильной и слабой связи. В первом случае электроны сильно связаны с положительными ионами и в качестве приближения для собственной функции может быть рассмотрено даваемое методом молекулярных орбит. Таким образом, металл рассматривается как огромная молекула. Во втором случае
638
основную роль играют плоские волны, на которые накладываются возмущения, вызываемые отклонениями от постоянства потенциала.
Что нового внесет периодичность потенциального поля, наличие малых потенциальных ящиков внутри металла?
Мы видели, что дискретность уровней в металле исчезает по мере увеличения его размера. Можно ожидать поэтому, что наличие малых потенциальных ящиков внутри металла должно привести к дискретности уровней. Однако в металле нет отдельных разделенных ящиков. Наоборот, для металла характерна легкость перехода электрона от одного атома к другому. Поэтому следует считать постоянный потенциал некоторым приближением к истинному. К этому потенциалу добавляется сравнительно малое периодическое поле. Мы должны рассмотреть, что нового внесет такое поле, как возмущение решения, полученного для постоянного потенциального поля.
Для простоты сначала рассмотрим случай линейного металла. В гл. XXII показано, что собственные функции электронов представляют собой периодические функции, описывающие электронные волны. Введем дополнительно к постоянному потенциалу некоторый периодический потенциал. Если такое дополнение (h) невелико по сравнению с первоначальным, то оно действует как возмущение.
Как указывалось в § 3 этой главы, в так называемом нулевом приближении принимается, что собственная функция не изменяется под влиянием возмущающего потенциала. Изменение энергии в нулевом приближении определяется величиной воздействия возмущающего потенциала h на частицу, описываемую этой невозмущенной функцией.
Это дополнение к энергии ео определяется, следовательно, величиной
ε0 = ∫ψ
hdτ,
где ψ0 - невозмущенная функция.
Для интересующего нас случая электронов металла расчет показывает, что ε0 = 0. Этот результат обязан периодичности функции ψ0, которая принимает то положительные, то одинаковые по величине, но отрицательные значения. Однако это не означает, что в нулевом приближении энергия возмущения равна нулю. Ситуация здесь аналогична возникшей в задаче о взаимодействии двух атомов водорода.
Как было показано в гл. XXIII, взаимодействие двух невозмущенных атомов водорода при условии неизменности
639
их функций (т.е. в нулевом приближении) очень мало. Оно определяется так называемым кулоновским взаимодействием и составляет лишь десять процентов энергии связи. Однако суперпозиции этих функций привели в рамках нулевого приближения (с неизменными функциями) к существенному расщеплению энергии на два уровня, значительно отстоящих от первоначального.
Близкая ситуация возникает и в задаче об электронах металла. Известно (см. гл. XXIV, § 1), что кристаллическая решетка приводит к отражению волн. Поэтому если соответствующие условия (условия Брегга) соблюдены, то наряду с падающей волной возникнет отраженная. Суперпозиция этих двух волн должна привести к расщеплению энергии. Следовательно, энергии электронов, отвечающие условию Брегга, благодаря этому расщеплению должны отсутствовать. Это условие для линейной задачи имеет следующий вид: 2d = nλ (XXIV.5).
Следует отметить, что такое расщепление имеет место и для волн, не точно, а приближенно отвечающих этому условию. Величина расщепления в этом случае не столь велика, как для волн, описываемых уравнением (XXIV.5), но в спектре энергии соответствующий уровень также исчезнет. Таким образом, в спектре энергии электронов должны возникнуть серии полос отсутствующих, т.е. запрещенных энергий. Этот результат может быть описан следующим образом.
Зависимость энергии электрона от длины волны выражается формулой
E =
·
=
k2,
где k = 1/λ - волновое число [см. формулы (XXII.2) и (XXII.3)].
Чтобы охватить электроны, движущиеся в обоих направлениях, следует считать, что k может иметь положительные и отрицательные значения. Для случая постоянного потенциала k может меняться непрерывно и зависимость энергии от k представится непрерывной параболической функцией (рис. XXIV.5).
Периодичность потенциала проявляется в ряде разрывов на кривой, изображенной на рис. XXIV.5, при значениях k, отвечающих условиям Брегга (рис. XXIV.6).
Таким образом, спектр энергии электрона состоит из разделенных зон, внутри которых энергия меняется непрерывно (зоны Бриллюэна).
640
В случае пространственной металлической решетки волна может распространяться в любом направлении, поэтому k является вектором.
Рассмотрим некоторое направление в пространстве. Распространяющаяся по этому направлению волна может отразиться от различных систем плоскостей. Так как величины
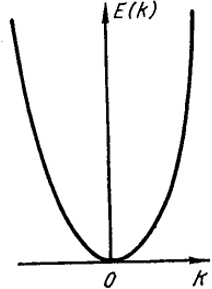
Рис. XXIV.5. Зависимость энергии электронов от волнового числа для совершенно свободных электронов
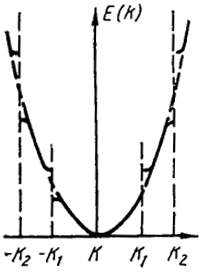
Рис. XXIV.6. Разрывы в энергии электрона, движущегося в периодическом поле
периодов решетки по различным направлениям неодинаковы, то значения k, отвечающие разрыву энергии, зависят от направления. Поэтому при малых разрывах энергии может оказаться, что энергия, запрещенная в одном направлении, разрешена в другом. Однако при больших разрывах некоторые уровни запрещены во всех направлениях.
Наличие зон разрешенных энергий для электронов металлов вытекает из самых различных приближенных рассмотрений металлов. Мы подойдем к энергетическому спектру электронов металлов, исходя из спектров разъединенных его атомов. В гл. XXIII было показано, что при образовании молекулы водорода энергия основного состояния атомов расщепляется на два уровня (E+ и E-). Аналогичное расщепление произойдет и с возбужденными термами атомов водорода. Расщепление на два уровня происходит потому, что суперпозиция двух состояний приводит к двум решениям для собственной функции молекулы и к двум уровням энергии.
641
Рассмотрим моль металла одновалентного элемента как огромную молекулу, возникающую в результате сближения NA атомов. Основной уровень атома при этом расщепится на NA весьма близких друг к другу уровней, которые составят первую бриллюэновскую зону. Таким образом, спектр уровней металла представляет собой как бы расщепленный (превращенный в зоны) спектр атома. Такой подход к объяснению зон показывает число состояний в зоне.
На уровнях зоны может поместиться 2NA электронов. Поэтому NA электронов, принадлежащие NA одновалентным атомам, могут заполнить только половину первой зоны.
Незаполненность зоны должна привести к электронной проводимости, т.е. должна быть характерна для металла. Если зона полностью заполнена, то проводимость должна отсутствовать и тело должно иметь свойство изолятора. Действительно, под влиянием электрического поля электроны должны начать двигаться к положительному полюсу и, следовательно, приобрести дополнительную энергию. При заполненной зоне электроны не могут поглотить малую энергию, так как принцип Паули запрещает переходы внутри заполненной зоны, а переход во вторую зону требует затраты большой энергии.
Таким образом, мы приходим к выводу, что одновалентные атомы должны образовать металлы, это действительно всегда выполняется. Двухвалентные атомы при образовании твердого тела в количестве одного моля представляют 2NA электронов, которые должны целиком заполнить первую зону. Таким образом, должен образоваться изолятор. Это на самом деле не выполняется, что связано с возможностью перекрывания различных зон.
Введение представления о зоне означает отказ от модели свободных электронов, движущихся в постоянном поле. Однако простая модель свободных электронов очень удобна для рассмотрения многих задач, связанных с движением электронов (электропроводность, рассеяние электронов, магнитные свойства и т.п.).
Можно показать, что приближенно модель свободных электронов применима для описания движения электронов, если ввести так называемую эффективную массу. Вдали от края зоны эффективная масса должна приближаться к массе электрона, а вблизи этого края должна возрастать и стремиться к бесконечности на самом крае. Это опишет неспособность электрона получать малые ускорения и увеличить
642
свою энергию, если его энергия отвечает началу запрещенной зоны. Теория показывает, что эффективная масса определяется плотностью состояний, т.е. числом энергетических уровней на единицу изменения энергии. Рассчитаем эту величину для свободных электронов Ферми:
E =
и d
E =
d
p.
Число состояний, приходящихся на интервал dp (см. гл. XIII) и рассчитанных на один атом (dnc), составляет
dnc =
d
p
или
В частности, для электрона уровня Ферми, т.е. обладающего наибольшей энергией:
=
√E.
и
=
(
)
1/3
.
Если подсчитать по этим формулам эффективную массу электрона, то она, естественно, совпадет с его гравитационной массой. Однако если уровень Ферми приближается к краю зоны, то плотность уровней уменьшается и возрастает эффективная масса. Эти величины могут быть определены из опытных данных, характеризующих одно свойство, и использованы для предсказания другого свойства.
Все обсуждение мы вели в рамках одноэлектронной задачи. В многоэлектронной задаче следует учитывать отталкивание электронов. Это может быть сделано в приближении так называемого самосогласованного поля. Для простоты рассмотрим это приближение для случая двух электронов. Будем считать, что первый электрон движется не только в поле внешнего потенциала, но учтем и его отталкивание от второго электрона, распределенного в пространстве в соответствй с функцией ψ2(2).
Подобное рассмотрение делается для собственной функции второго электрона ψ2(2). Таким образом, уравнения
643
записываются для трехмерного, а не шестимерного пространства. Это приближение было дано Гартри. С точки зрения вариационного принципа оно отвечает собственной функции в виде произведения ψ1(1)ψ2(2), дающего наименьшую энергию. Однако в этом приближении не соблюдено условие тождественности электронов, т.е. не введен член, отвечающий их обмену. Такое приближение было сделано Фоком. Поэтому метод самосогласованного поля называется методом Гартри-Фока. В дальнейшем мы будем вести изложение в рамках этого метода.
Основной целью квантово-механического рассмотрения металлов является расчет зонной структуры. Наиболее простым является приближение почти свободных электронов, в котором собственная функция разлагается по функциям плоских волн. Коэффициенты при этом разложении получаются на основе решения уравнения Шредингера с потенциалом свободных атомов. Для решения возникающих сотен линейных уравнений используются вычислительные машины. Медленная сходимость связана с тем, что вблизи сердцевины ионов волновые функции электронов проводимости имеют сильные осцилляции, отвечающие собственным функциям атомов. Чтобы их описать в рамках разложения по плоским волнам, нужно вводить в разложение большое число плоских волн. Положение существенно улучшается в методе ортогонализованных плоских волн. В этом методе функции, описывающие плоские волны, ортогонализируются но отношению к собственным функциям электронов внутренних оболочек ионов. Как указывалось, ортогональность функций в квантовой механике означает, что они "разные".
Пусть функции ψ1 и ψ2 не ортогональны и ∫ψ1ψ2dτ = S, S ≠ 0. Сконструируем вместо ψ1 функцию ψ1 = ψ1 - Sψ2. Нетрудно заметить, что ∫ψ
ψ
2dτ = 0. Действительно:
∫ψ
ψ
1dτ =
∫ψ
1ψ
2dτ -
S∫ψ
dτ = 0.
В качестве базиса разложения искомой функции электронов берутся в методе ортогональных плоских волн (ОПВ) функции плоских волн, ортогонализированных по отношению функций, описывающих внутренние электроны оболочек ионов. Таким образом, осцилляция функций базиса вблизи ионов уменьшается, так как она учтена уже в самом базисе. Это приводит к существенному сокращению необходимых членов в разложении (до 30-50),
644
Для электронов металла характерно наличие двух различных областей - между и вблизи ионов. В методе присоединенных плоских волн (ППВ) вводятся различные потенциалы - внутри сфер некоторого радиуса потенциал, обладающий сферической симметрией, а между ионами - постоянный. Собственные функции для одинаковой задачи, отвечающие этим потенциалам, сходятся на границах. Этот метод еще существенно снижает число членов в разложении.
К этому методу примыкают два других - метод ячеек Вигнера и Зейтца и получивший большое распространение в последнее время метод псевдопотенциала. В методе Вигнера и Зейтца предложен способ составления модифицированных атомных функций. На электрон, находящийся вблизи иона, действуют поля этого иона и всех остальных. Поле одного иона обладает (за некоторым исключением) сферической симметрией. Поле всех остальных ионов решетки в случае высокой симметрии решетки в некотором приближении можно считать обладающим сферической симметрией.
Таким образом, в каждой ячейке, на которые можно разбить металл, действует свое, обладающее сферической симметрией поле. Такие ячейки в случае элементов представляют собой многогранники, составленные из плоскостей, перпендикулярных линиям, соединяющим центральный атом с соседями и делящими межатомные расстояния пополам.
Важным отличием собственных функций, описывающих поведение функций в ячейке, от атомных являются краевые условия. В случае атома эти условия сводятся к требованию равенства функций нулю на бесконечно большом расстоянии от центра.
Для функций описывающих электрон в ячейке металла, необходимо потребовать непрерывности функции и ее первой производной на границе между соседними многогранниками. Кроме того, должны удовлетворяться требования симметрии, которые мы разберем на примере щелочных металлов.
Как указывалось в § 5 этой главы, все щелочные металлы образуют объемноцентрированную кубическую решетку. В этом случае ячейка представляет собой полиэдр, который с достаточной точностью может быть заменен сферой равного объема.
Так как функция должна симметрично повторяться в следующей ячейке, то необходимо потребовать, чтобы
645
на границе сферы (r = rs) соблюдалось равенство
∂ψ/∂r = 0.
(XXIV.6)
Таким образом, основное отличие собственных функций, описывающих поведение электрона в металле, от атомной функции сводится к условию (XXIV.6), определяющему переход электрона в следующую ячейку.
Потенциальная энергия в уравнении Шредингера для ячейки подбирается таким образом, чтобы решение этого уравнения с краевыми условиями, отвечающими задаче атома (ψ∞ = 0), правильно передало термы атома. Так, найденное потенциальное поле содержит приближенное описание эффективного отталкивания валентного электрона от электронов ионов.
Наряду с расчетом кулоновской и объемной энергий при вычислении необходимо учитывать выигрыш энергии, который возникает подобно тому, как это происходит при действии дисперсионных сил в результате стремления электронов избегать друг друга (энергия корреляции).
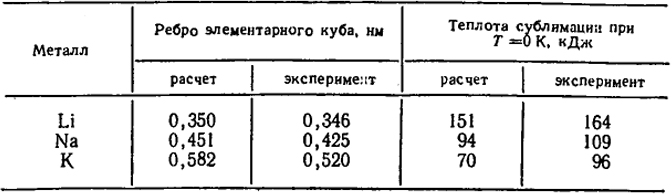
Такого типа расчеты для энергии и периода решетки дают удовлетворительные результаты, особенно для лития и натрия, как это видно из табл. XXIV.3.
Метод псевдопотенциала также основывается на рассмотрении пространства между ионами и областей вблизи ионов. При этом существенно, что энергетический спектр электронов металла довольно близок к получаемому из приближения свободных электронов. Электрон при приближении к положительному иону ускоряется и поэтому большую часть времени проводит между ионами. Между тем, в отличие от энергетического спектра собственная функция вблизи иона существенно отличается от соответствующей свободным электронам, так как возникают осцилляции, отвечающие атомным функциям.
Таблица XXIV.3. Сравнение экспериментальных значений постоянной решетки и теплоты сублимации с результатами квантово-химического расчета
646
В методе псевдопотенциала собственные оДноэлектрон-ные функции описывают как сердцевину, так и середину между ионами с помощью одного эффективного потенциала. При этом стремятся к гладкости функций в сердцевине. Чтобы учесть малое время пребывания электрона в сердцевине (эффективное отталкивание), ставится требование ортогонализации "псевдофункции" и функций сердцевины. Поэтому, строго говоря, нельзя записать уравнение Шредингера с локальным потенциалом, т.е. зависящим от координат. В уравнении √φ + (8π2m/h2)(E - W)φ = 0 W носит название псевдопотенциала и не является локальным, хотя часто W в известном приближении используют как локальную. Псевдопотенциал должен близко передавать собственные значения уравнения с истинным потенциалом. Псевдопотенциал является слабым по сравнению с истинным и поэтому ряды, соответствующие теории возмущений, быстро сходятся. В псевдопотенциал можно вводить подгоночные параметры, определяемые из опыта, и, таким образом, связывать один опыт с другим. В качестве примера приведем псевдопотенциал отдельного иона, содержащего только заполненные оболочки. Принимается, что за пределами некоторого радиуса R действует обычный потенциал электростатического взаимодействия -Ze2/r, а внутри псевдопотенциал имеет постоянное значение. Важной характеристикой металлов является электропроводность.
Впервые электронная теория проводимости металлов была развита П. Друде.
Под влиянием поля Е электрон движется, ускоряясь, на расстоянии, определяемом длиной пути его свободного пробега (l). Если скорость электрона υ, то время между двумя столкновениями равно l/υ. Ускорение электрона определяется отношением силы, на него действующей, к его массе, т.е. величиной Ее/т. Следовательно, под влиянием поля электрон получает скорость порядка Eelυ/mυ.
Перенос тока электронами определяется произведением их числа в единицах объема (п) на заряд и на среднюю скорость.
Следовательно:
i = n(Ee2l/mυ).
Отсюда удельное сопротивление р следующим образом связано с характеристиками электрона:
ρ ∼ mυ/ne2l.
(XXIV.7)
Друде, полагая, что электроны сталкиваются с атомом,
647
принял, что l ≈ 10-8 см. Скорость он вычислил в соответствии с законом распределения по степеням свободы:
mυ2/2 = 3/2kT.
(XX1V.8)
Поучительно, что, сделав эти совершенно неправильные предположения, получают разумные значения для сопротивления некоторых металлов (например, меди) при комнатной температуре.
Однако эта теория дает неправильную температурную зависимость сопротивления. Согласно уравнениям (XXIV.7) и (XXIV.8), сопротивление должно расти пропорционально корню из температуры, между тем обычно имеет место линейная зависимость между сопротивлением чистых металлов и температурой.
Уравнение (XXIV.8) приводит к наличию электронной теплоемкости, что также противоречит опыту.
Зоммерфельд построил теорию электропроводности металлов на основе квантовой теории электронного газа.
Как вы видели, электронный газ практически полностью при комнатной температуре находится в состоянии вырождения, поэтому скорость электронов не зависит от температуры. Температурная зависимость сопротивления определяется температурной зависимостью величины l. Так как скорость рассчитанная по уравнению для ферми-газа, приблизительно в 100 раз больше скорости, рассчитанной по формуле (XXIV.8), то для сохранения правильного значения сопротивления необходимо, чтобы длина пути свободного пробега была в 100 раз больше межатомного расстояния.
Это обстоятельство связано с тем, что представление о столкновениях между электронами и ионами слишком упрощено. Речь может идти о рассеивании электронов кристаллической решеткой, при котором часть их энергии будет передаваться атомам решетки. Однако при абсолютном нуле, когда атомы решетки находятся в покое, этого рассеивания нет. Действительно, длина волны электрона (вдали от края зоны) велика по сравнению с периодом решетки и поэтому явления дифракции отсутствуют. Рассеяние электронов, а следовательно, и сопротивление металлов вызывается прежде всего нарушением идеальности решетки, вызываемым тепловыми колебаниями.
Рассеяние электронов может происходить также на примесях или дефектах решетки.
Мы вернемся к вопросам, рассмотренным в этом параграфе, при обсуждении полупроводников (§ 5 этой главы).
648
