Прочность ионной решетки определяется прежде всего электростатическим взаимодействием. Как и в случае ионных молекул, отталкивание не вносит никакого вклада в энергию решетки, если следовать приближенно твердых шаров. Если отталкивание описывать законом
, то
634
энергия электростатического притяжения должна быть умножена на (1 -
) (см. гл. XXIII).
Рассмотрим для конкретности решетку хлористого натрия. На рис. XXIV.4 схематически изображена эта решетка (черные кружки - ионы хлора).
Определим энергию электростатического взаимодействия одного выбранного иона с остальными. В первой координационной оболочке, как это видно из рис. XXIV.4, находятся шесть ионов противоположного знака. Энергия взаимодействия центрального иона с ними равна 6e2/d, где d - период решетки.
На расстоянии d√2 от центрального иона находятся 12 ионов того же знака, дающих вклад в энергию, равный 12e2/d√2.
Следующая координационная оболочка содержит 8 ионов, имеющих заряд, противоположный по знаку заряду центрального иона, и находящихся на расстоянии, равном d√3.
Суммирование всех этих слагаемых дает медленно сходящийся ряд
-
(6 -
+
-
+
- ...).
Энергию решетки мы получим, если умножим это выражение на число ионов в грамм-молекуле решетки (2NA) и разделим результат на два, поскольку мы дважды учитывали взаимодействие каждой пары ионов.
Таким образом:
U = -(NAe2/d)(6 - 12√2 + 8/√3 + ...).
Величина, находящаяся в скобках, носит название постоянной Маделунга (а). Разработаны математические методы расчета этой величины для разного типа решеток.
Следовательно:
U = -NAe2a/d.
(XXIV.3)
Для решетки типа NaCl a = l,75.
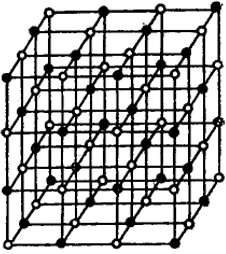
Рис. XXIV.4. Структура NaCl
635
Расчеты чисел Маделунга для разных решеток показывают, что энергия взаимодействия одного иона решетки с остальными мало зависит от природы решетки. Другими словами, отношение постоянной Маделунга к числу ионов (m) в формульной единице есть величина приблизительно постоянная.
Мы приходим, таким образом, к приближенной формуле А.В. Капустинского для энергии решетки:
U = -1076
кДж/моль,
где Z1 и Z2 - заряды ионов; ra и rb - их радиусы, нм.
Формула (XXIV.3) передает энергию решетки в приближении модели твердых шаров.
Энергия решетки может быть рассчитана из экспериментальных значений энергии образования твердых веществ из элементов. Так, энергия решетки U может быть найдена из теплоты реакции
Naт + 1/2Cl2г = NaCl + Qобр.
Для этого, в соответствии с законом Гесса (см. гл. I), надо просуммировать следующие уравнения:
Na+ + e = Naг + V;
Naг = Naт + σ;
Cl- = Cl + e - A;
Cl = Cl2г + D/2;
Naт + 1/2Cl2г = NaClт + Qобр,
где V - потенциал ионизации атома натрия; А - энергия сродства атома хлора к электрону; σ - теплота сублимации твердого натрия; D - энергия диссоциации молекулы Сl2.
Суммирование приводит к уравнению
Na+ + Сl- = NaClт + V + σ - A + D/2 + Qобр.
Таким образом:
-U = V + σ - A + D/2 + Qобр.
(XXVI.4)
В табл. XXIV.2 дано сопоставление энергий решеток, вычисленных по формуле (XXIV.3) с учетом отталкивания и найденных из экспериментальных данных по формуле (XXIV.4).
636
Таблица XXIV.2. Энергия решеток, вычисленная и экспериментальная
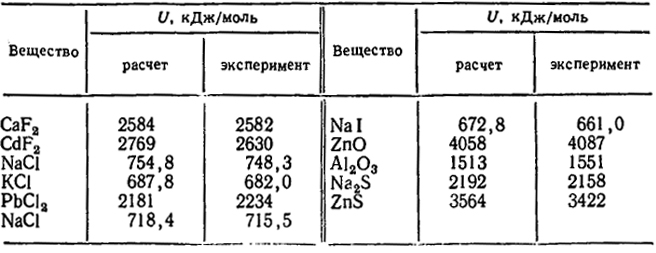
637
