Основное отличие твердых кристаллических тел заключается в анизотропии свойств. Эта анизотропия является следствием правильного расположения атомов, образующих кристаллическую решетку.
В 1912 г. М. Лауэ доказал, что рентгеновские лучи представляют собой электромагнитное излучение, длина волны которого примерно в 10000 раз меньше длины волны видимого света; этим были созданы основы структурного рентгеновского анализа.
У.Л. Брегг и У.Г. Брегг и несколько позднее Г.В. Вульф вывели основную формулу, позволяющую расшифровывать структуру по данным интерференции рентгеновских лучей. Любую кристаллическую решетку можно рассматривать как совокупность плоскостей, находящихся на одинаковом расстоянии друг от друга. Пусть рентгеновский луч падает, как это показано на рис. XXIV.1, под определенным углом скольжения 9 к плоскости (угол скольжения является дополнительным к углу между лучом и перпендикуляром к плоскости).
Из рис. XXIV.1 видно, что в точке С произойдет интерференция луча, отразившегося от верхней плоскости, и луча, отразившегося от следующей плоскости. Разность хода этих двух лучей Δ, как это следует из рис. XXIV.1, равна Δ = АВ + АС. Если Δ равна целому числу волн, то рассматриваемые два луча будут максимально усиливать друг друга.
Из рис. XXIV.1 видно, что AC = AD и Δ = BD = 2dsinθ. Таким образом,
628
наибольшее отражение должно наблюдаться, если угол 8 будет подчиняться условию
2αsinθ = nλ.
(XXIV.1)
Измеряя зависимость интенсивности отраженного луча от угла скольжения, можно определить величину периода решетки и ее кристаллическую структуру.
Такой метод, при котором на монокристалл направляют монохроматические рентгеновские лучи (получаемые при падении катодных лучей
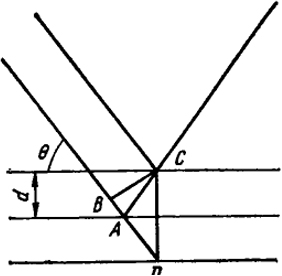
Рис. XXIV.1. Отражение рентгеновских лучей от плоскостей кристалла
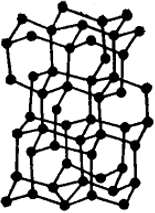
Рис. XXIV.2. Решетка алмаза
на металлический антикатод), был предложен У.Л. Бреггом и У.Г. Бреггом. В их первоначальных опытах кристалл был неподвижным и для варьирования угла вращалась регистрирующая отраженные лучи ионизационная камера. Вместо этого можно поворачивать кристаллическую плоскость в определенных пределах. Отраженные лучи при этом будут регистрироваться камерой или фотографироваться на пленке.
В варианте М. Поляни монокристалл вращается, делая полный оборот во время съемки, так что рентгеновские лучи отражаются разными плоскостями кристалла.
В наиболее распространенном методе П. Дебая и А. Шерера используют прессованный мелкий порошок, который помещают в тонкостенную трубку и устанавливают перпендикулярно направленную рентгеновского луча. Цилиндрическая фотографическая пленка окружает эту трубку. В беспорядочно расположенных кристалликах всегда найдутся плоскости, расположение которых удовлетворяет условию (XXIV.1). В результате этого в определенных направлениях образуются максимумы интенсивности отраженного излучения.
Огромный материал по структуре различных соединений, собранный исследователями, стал одной из основ кристаллохимии.
Структура решетки вещества определяется условиями минимума свободной, а при низкой температуре - внутренней энергии. Атомы стремятся расположиться таким образом, чтобы энергия взаимодействия была возможно больше.
629
По характеру энергии взаимодействия между атомами кристаллические решетки могут быть разбиты на следующие группы: 1) атомные, 2) металлические, 3) ионные, 4) молекулярные.
В атомных решетках между атомами осуществляются гомеополярные связи. Естественно поэтому, что характер решетки (число и расположение соседей около каждого атома) определяется числом и расположением валентностей. На рис. XXIV.2 изображена структура алмаза (характерная вообще для элементов четвертой группы периодической системы - кремния, германия и серого олова). Каждый атом углерода располагается в центре тетраэдра и направляет свои четыре σ-связи к четырем соседям.
Многие металлоиды (С, Si, Ge, As, Sb, P, Се, Те и т.д.) кристаллизуются таким образом, чтобы каждый атом имел 8–N соседей, где N - номер группы периодической системы, в которую входит атом. Так, Se и Те, принадлежащие к шестой группе, образуют в кристаллической структуре спиральные цепочки, в которых каждый атом имеет по два соседа; в структурах мышьяка, сурьмы и висмута каждый атом имеет по три соседа. "Правило 8–N" может быть понятно как результат тенденции атома достроить свою внешнюю электронную оболочку до устойчивой, содержащей восемь электронов.
В металлических решетках электроны обобществлены, поэтому энергия связи в решетках металлических элементов определяется общей электронной плоскостью.
Наиболее плотная упаковка шаров на плоскости может быть достигнута при размещении их по гексагональной схеме, когда каждый шар соприкасается с шестью соседями (рис. XXIV.3).
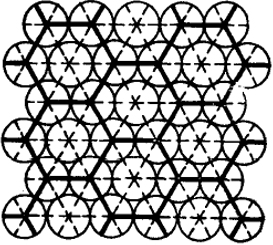
Рис. XXIV.3. Слой плотноупакованных шаров
При плотной упаковке в пространстве координационное число достигает двенадцати. Можно получить такую упаковку следующим образом: шесть шаров окружают центральный в одной плоскости. Шары в верхнем слое могут размещаться в углублениях между шарами в плотно упакованном слое. Вокруг каждого шара имеются шесть таких углублений (см. рис. XXIV.3). Однако поместиться в них могут только три шара, которые окажутся над центрами треугольников, вершины которых расположены либо вниз, либо вверх. Обе упаковки будут плотными.
Пусть для конкретности шары во втором слое расположены над центрами треугольников, направленных вниз. При укладке третьего слоя снова возникнут две возможности. Если шары третьего слоя окажутся над центрами треугольников второго слоя, вершины которых направлены вниз, то возникнет гранецентрированная кубическая структура.
630
Если будут заниматься места над центрами треугольников второго слоя с вершинами, направленными вверх, то возникнет плотноупакованная гексагональная структура. При этом над каждым шаром в первом слое будет шар в третьем.
За редкими исключениями, элементы, обладающие свойствами металлов, кристаллизуются в одной из трех решеток: плотной гексагональной (Be, Mg, Zn, Cd, Ti...), гране-центрированной кубической (Cu, Ag, Au, Al, γ-Fe, β-Co, Ni) и объемноцентрированной кубической (Li, Na, α-Cr, α-Fe, Mo, W).
В ионных кристаллах, например солях, энергия определяется в основном электростатическим взаимодействием ионов. Их пространственное расположение определяется в первую очередь особенностями плотной упаковки шаров разного размера. Если один из ионов меньше другого (например, в CsCl), то координационное число 12 не может осуществиться. В решетке CsCl ион цезия находится внутри куба, в вершинах которого находятся ионы хлора. Координационное число цезия в нем равняется восьми. Если отношение радиуса катиона к радиусу аниона еще уменьшается, то восемь соседей не могут уместиться вокруг маленького иона и осуществляется решетка типа простой кубической решетки NaCl, в которой в вершинах куба попеременно располагаются ионы хлора и натрия. Координационное число при этом уменьшается до шести. Если рассматриваемое отношение еще меньше, то образуется решетка с координационным числом четыре (например, ZnS имеет решетку типа алмаза с чередующимися атомами серы и цинка).
Радиусы ионов и атомов определяют по величине межатомного расстояния в кристаллах или молекулах, представляя это расстояние как сумму радиусов. Радиусы атомов могут быть определены как половина расстояния в симметричных молекулах с одинарной связью или из расстояния между одинаковыми соседними атомами в многоатомных молекулах.
Если весьма приближенное представление об аддитивности радиусов выполняется, то расстояние в любой молекуле или атомном кристалле равно сумме радиусов атомов.
Для примера можно привести величины радиусов атомов для одинарной связи, вычисленные из разных данных, нм: Н - 0,031; Li - 0,134; Be - 0,107; В - 0,089; С - 0,077; N - 0,070; O - 0,066; F - 0,064; Na - 0,154; Mg - 0,140;
631
Al - 0,126; Si - 0,117; P - 0,110; S - 0,104; Cl - 0,099; Cu - 0,135; Zn - 0,131; Ca - 0,126; Ge - 0,122; As - 0,121; Se - 0,117; Br - 0,114; Ag - 0,153; Cd - 0,148; In - 0,144; Sn - 0,140; Sb - 0,141; Те - 0,157; I - 0,133; Au - 0,150; Hg - 0,148; Ti - 0,147; Pb - 0,146; Bi - 0,151. Радиусы в двойных r(2) и тройных r(3) связях определяются следующими приближенными соотношениями [r(1) - расстояние в одинарной связи]:
r(2) = 0,90r(1); r(3) = 0,79r(1)
Значительные отклонения межатомных расстояний от суммы радиусов позволяют судить о характере связи. Так, например, для СО согласие с аддитивной схемой получается лишь, если принять наличие тройной связи.
Определение значений радиусов в ионных соединениях требует какой-либо гипотезы, так как опыт дает расстояние лишь между разными ионами. Составлено несколько таблиц радиусов ионов. В одной из них принято, что в решетках с большим анионом и маленьким катионом (например, в LiI) соприкасаются анионы. Поэтому радиус I- находится как половина соответствующего расстояния. В других таблицах используются какие-либо физические характеристики ионов, зависящие от их радиусов (например, в гл. XXV будет показано, что рефракция ионов пропорциональна кубу радиуса).
В табл. XXIV.1 даны значения радиусов (по Раису) ионов, имеющих электронную структуру атомов инертного газа.
Полингу принадлежит следующее полуэмпирическое рассмотрение радиусов атомов в металлах. Он принимал, что в металлах имеет место суперпозиция различных сеток валентных гомеополярных связей в духе описанной в гл. XXIII теории резонанса валентных структур. При этом рассмотрении можно говорить о средней кратности связей в металле.
Полинг прежде всего устанавливает эмпирическое соотношение между атомным расстоянием r и числом связей п:
r(1) - r(n) = 0,03ln n.
(XXIV.2)
Это уравнение удовлетворительно описывает расстояние в связях:
C - Cr(1) = 0,1542 нм; C = Cr(2) = 0,1350 нм;
С ≡ Cr(3) = 0,1204 нм; в бензоле r(1,5) = 0,1418 нм.
632
Таблица XXIV.1. Ионные радиусы, нм

633
В качестве примера применения уравнения (XXIV.2) к металлам рассмотрим межатомное расстояние в цирконии, который кристаллизуется в двух формах: объемно-центрированной кубической и плотноупакованной гексагональной.
Определим на основе концепции Полинга радиус атомов циркония в гексагональной решетке, считая заданным этот радиус в кубической. Из величины периода этой решетки (0,361 нм) можно определить радиус для восьми кратчайших связей, направленных к вершинам куба (0,1563 нм), и для шести более отдаленных (0,1805 нм).
Валентность циркония равна четырем. Определим, какая часть этих валентностей приходится на восемь ближайших соседей (x) и на шесть более отдаленных (4 - х).
На каждую ближайшую связь приходится х/8 связей и, согласно уравнению (XXIV.2), получим
r(1) - r(
) = 0,03 ln
,
аналогично для отдаленных связей:
r(1) - r(
) = 0,03 ln
.
Учитывая, что r(
) = 0,1563, нм, а
r(4 -
x|6) = 0,1805 нм, получим
x = 0,358 нм и
r(1) = 0,1454 нм.
Значение r(1) позволяет определить радиус в гексагональной решетке. Действительно, в этом случае на одну связь приходятся 4/12 = 1/3 связей. Согласно уравнению (XXIV.2):
r(1) - r(
) = 0,03 lg
.
Отсюда r(
) = 0,1601 нм, что близко к опытной величине 0,1597 нм.
634
