Как неоднократно упоминалось, в различных физических процессах (конденсации, адсорбции и др.) существенную роль играют молекулярные силы, приводящие на больших расстояниях к притяжению между насыщенными молекулами. Они отличаются от сил, определяющих химическое взаимодействие, прежде всего в следующих трех отношениях:
- 1) по величине энергии молекулярное взаимодействие меньше энергии химического приблизительно на один порядок;
- 2) силы химического сродства специфичны, а силы молекулярного притяжения универсальны. Любые атомные системы притягиваются на больших расстояниях. Это обстоятельство следует из того, что все газы конденсируются при достаточно низких температурах;
- 3) в отличие от химических сил, обладающих насыщаемостью, основной тип молекулярных сил характеризуется аддитивностью. Это означает, что энергия взаимодействия двух молекул не зависит от присутствия третьей.
Подобно делению сил химического сродства на гетеро- и гомеополярные молекулярные силы делятся на три вида:
- а) ориентационные силы возникают между молекулами, обладающими асимметрией, за счет электростатического взаимодействия зарядов, из которых состоят молекулы;
619
- б) индукционные силы действуют между дипольной молекулой и недипольной в результате поляризации недипольной в поле, создаваемой дипольной;
- в) дисперсные силы обязаны специфическому взаимодействию электронов молекул.
Рассмотрим наиболее простой случай такого взаимодействия для двух атомов водорода, находящихся на столь больших расстояниях, что электроны остаются в атомных состояниях и не переходят на молекулярные орбиты. В каждом атоме центр тяжести отрицательного заряда совпадает с центром тяжести положительного (ядром). Таким образом, атомы не имеют дипольных моментов. Однако в каждый данный момент времени атомы обладают "мгновенным" дипольным моментом. Система будет обладать более низкой энергией, если эти моменты будут ориентированы в пространстве определенным образом. Так, если в одном атоме электрон находится слева от ядра, то и в другом для уменьшения отталкивания электрону выгоднее тоже быть слева.
Таким образом, электроны разных атомов в какой-то степени должны двигаться в такт. Это означает, что в разных атомах чаще должны быть представлены конфигурации электронов, приводящие к меньшему отталкиванию.
Ориентационные силы получили свое название потому, что молекулы должны ориентироваться в пространстве энергетически выгодным образом.
Представим себе две дипольные молекулы. На рис. XXIII.5 показана энергетически более выгодная их конфигурация.

Рис. XXIII.5. Две ориентированные дипольные молекулы
Очевидно, если температура достаточно низка, то осуществится ориентация и, следовательно, притяжение молекул. При очень высокой температуре энергия вращения будет больше энергии взаимодействия, ориентация исчезнет и молекулы не будут притягиваться друг к другу.
Таким образом, Ориентационные молекулярные силы зависят от температуры и уменьшаются при ее возрастании. Мы рассмотрим два предельных случая очень низких и очень высоких температур.
620
При очень низких температурах, когда энергия притяжения существенно больше kT, произойдет полная ориентация молекул. Тогда, например, взаимодействие молекул, находящихся на одной линии на расстоянии R друг от друга, опишется как взаимодействие зарядов (см. рис. XXIII.5):
ε =
+
+
-
,
где Δ1 и Δ2 - расстояния между центрами тяжести зарядов, равных по величине е. Считая, что эти расстояния малы по сравнению с K, получим:
ε = -2RΔ1Δ2e2/R4.
По определению μ1 = Δ1e и μ2 = Δ2e, где μ1 и μ2 - дипольные моменты молекул. Тогда
ε = -2μ1μ2/R3.
(XXIII.19)
Мы видим, что при низких температурах энергия притяжения дипольных молекул обратно пропорциональна кубу расстояния.
Рассмотрим сначала индукционные силы, а затем вернемся к асимптотическому выражению ориентационных сил при высоких температурах. Для простоты рассмотрим случай, когда недипольная молекула находится на линии, на которой расположен вектор, характеризующий дипольный момент. Под влиянием электрического поля, создаваемого дипольной молекулой, в недипольной молекуле возникает вследствие поляризации электронов наведенный момент μн, определяемый формулой μн = αF, где α - поляризуемость
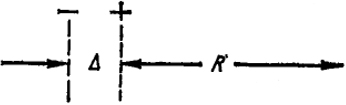
Рис. XXIII.6. Схема для расчета напряжения поля диполя
недипольной молекулы; F - напряжение поля, создаваемого дипольной молекулой на расстоянии R. Из рис. XXIII.6 видно, что
F =
-
=
=
.
(ХХIII.20)
где μ - дипольный момент молекулы.
Следовательно, μн = 2αμ/R3.
621
Так как направление наведенного момента μн противоположно направлению μ, то энергия их взаимодействия может быть рассчитана по формуле (XXIII. 18). Следовательно:
ε = -4αμ2/R6.
(ХХIII.21)
Необходимо, однако, учесть, что поляризация электрона требует затраты некоторой энергии. Для расчета этой энергии будем непрерывно изменять напряженность поля от нуля до конечного значения F. Энергия взаимодействия ориентированного диполя μ с полем равна μF.
Действительно, энергия взаимодействия двух зарядов диполя с полем, определяемая уравнением
εп = eV1 - eV2 = e(V1 - V2),
где V1 и V2 - значения потенциала поля в точках, в которых находятся центры тяжести положительного и отрицательного зарядов.
Однако V1 - V2 = -FΔ. Таким образом:
εп = -FeΔ = -μF.
(XXIII.22)
Изменение F на dF потребует затраты энергии μdF. Общая затрата энергии на поляризацию молекулы выразится следующим образом:
ε = -αμ2/R6.
(XVIII.23)
Подставив значение F по формуле (XXIII.20), получим для рассматриваемой энергии 2αμ2/R6.
Таким образом, половина выигранной энергии взаимодействия затратится на поляризацию. Окончательно вместо уравнения (XXIII.21) получим ε = -2αμ2/R6.
Итак, энергия индукционного взаимодействия не зависит от температуры и обратно пропорциональна шестой степени расстояния между молекулами.
Для получения средней энергии индукционного взаимодействия молекул, произвольно расположенных в пространстве, необходимо найти напряжение поля F, усредненное по различным углам между линией, соединяющей молекулы, и направлением дипольного момента. После расчета
ε = -αμ2/R6.
(XXIII.23)
Расчет энергии индукционного взаимодействия позволяет вычислить ориентационное взаимодействие на основе следующей аналогии.
622
Дипольная молекула, ориентируясь под влиянием поля F, образует некоторое среднее, зависящее от температуры значение проекции момента против направления поля. Мы покажем, что эта проекция пропорциональна F. Таким образом, возникает некоторый аналог поляризуемости.
Для определения этой зависящей от температуры эффективной поляризуемости определим среднее значение проекции момента молекулы на ось поля. Проекция момента (m) определяется углом θ между ними и направлением поля, т.е.
m = μcosθ.
(ХХIII.24)
Для определения среднего значения m (т) надо вычислить вероятность образования угла, лежащего между значениями θ и dθ.
Геометрическая вероятность иметь такой угол (dωг) определяется отношением поверхности шарового пояса, отвечающего этому углу, ко всей поверхности шара единичного радиуса (рис. XXIII.7):
dωг =
=
sinθdθ.
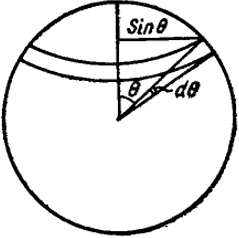
Рис. XXIII.7. Схема для расчета геометрической вероятности угла θ
Наряду с геометрической вероятностью необходимо учесть, что энергия взаимодействия (ε) момента μ с полем зависит от угла θ.
Действительно, согласно уравнению (XXIII.22), ε = = -Fm. Учитывая выражение (ХХIII.24), получим ε = Fμcosθ. По закону Больцмана (см. гл. XI) получим общую вероятность
dω =
sinθdθe
Fμcosθ/kT.
Таким образом;
623
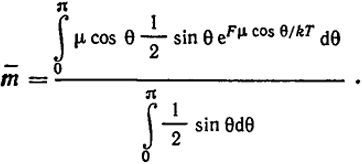
Полагая, что kT ≫ Fμcosθ, разлагая экспоненту в ряд и ограничиваясь двумя -членами, получим
m = -μ2F/3kT.
(XXIII.25)
Таким образом, согласно уравнению (XXIII.22), значение эффективной поляризуемости а определится уравнением
α = μ2/3kT.
(XXIII.26)
Подставив это выражение в уравнение для индукционного взаимодействия, получим приближенное выражение для ориентационного взаимодействия:
Приближенность приведенного расчета определяется тем, что мы взяли среднее значение поля, создаваемого первой молекулой, и не провели детального расчета вероятности различных взаимных ориентации дипольных моментов. Такой расчет дает
εор ≈ (μ
μ
/kT)(1/R6).
(XXIII.27)
Таким образом, ориентационное взаимодействие при высоких температурах обратно пропорционально температуре и шестой степени расстояния между молекулами.
Третий вид сил молекулярного взаимодействия - дисперсионные силы - можно рассматривать как некоторый аналог ориентационных сил. Мы можем поэтому приближенно получить выражение для этих сил на основе формулы (XXIII.27). Для этого необходимо определить аналоги величин kT и μ, входящих в это уравнение.
Ограничимся при этом рассмотрением взаимодействия одинаковых молекул. Произведение kT характеризует энергию теплового движения, препятствующего ориентации при взаимодействии дипольных молекул. Мгновенным электронным моментам мешает ориентироваться их кинетическая энергия, являющаяся частью нулевой энергии.
Как мы видели ( см. гл. XXII), кинетическая энергия равна по величине энергии; мерой ее может быть потенциал
624
ионизации V. Поэтому вместо kT мы подставим в выражение (XXIII.27) V. Вместо мгновенного дипольного момента целесообразно ввести экспериментально определяемую, зависящую от него величину. В рамках той же модели "мгновенных моментов" рассмотрим поляризуемость молекулы. Согласно уравнению (XXIII.26), дипольная молекула при температуре Т имеет эффективную поляризуемость α = μ2/3kT. Следовательно, молекула с мгновенным дипольным моментом μ должна иметь поляризуемость
α = μ2/3V.
Вместо kT, согласно изложенному выше, мы ввели потенциал ионизации V.
Таким образом, подставляя в уравнение (XXIII.27) выражения для V и μ2, мы получим (опуская численный множитель)
ε ≈ -α2V/R6.
Точная формула для одинаковых атомов имеет вид
ε = -3α2V/4R6.
Вазимодействие разных атомов описывается следующей формулой Ф. Лондона:
ε =
·
·
.
(XXIII.28)
Слетер и Кирквуд связали энергию дисперсионного взаимодействия с числом внешних электронов N.
Для взаимодействия одинаковых атомов
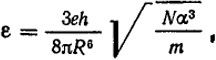 (XVIII.29)
(XVIII.29)
где т - масса электрона.
Дисперсионные силы не зависят от температуры. Они универсальны, так как существуют в любых системах, где имеются электроны. Движение электронов "в такт" представлено лишь в слабой степени, т.е. благодаря высокой нулевой энергии электроны одной молекулы в малой степени учитывают мгновенное положение электронов другой молекулы. Результатом этого является аддитивность дисперсионных сил. Электроны одной молекулы могут учитывать положение электронов нескольких соседних молекул, что было бы, конечно, невозможно при движении электронов в такт.
625
Расчеты показывают, что индукционные силы малы по сравнению с ориентационными и дисперсионными и ими можно пренебречь.
Для молекул, не имеющих дипольных моментов, единственным видом молекулярных сил являются дисперсионные. Из формулы (XXIII.29) следует, что дисперсионные силы растут с числом электронов. В этом заключается основная причина таких фактов, как, например, возрастание температур кипения при увеличении молекулярной массы углеводородов.
У дипольных молекул ориентационные силы сравнимы с дисперсионными. Относительная роль дисперсионных сил определяется обычно числом электронов. Так, во взаимодействии молекул воды дисперсионные силы почти не играют роли. При отсутствии дипольного момента вода имела бы температуру кипения, близкую к температуре кипения кислорода. В метиловом спирте роль дисперсионных сил увеличивается, а в этиловом дисперсионный эффект сравним с ориентационным. Так как дипольный момент у всех этих молекул одинаков, то рассматриваемое явление обязано увеличению молекулярной массы.
Развитие теории молекулярных сил позволило провести расчеты теплот конденсаций, теплот адсорбции, ассоциаций, ван-дер-ваальсовых постоянных и пр.
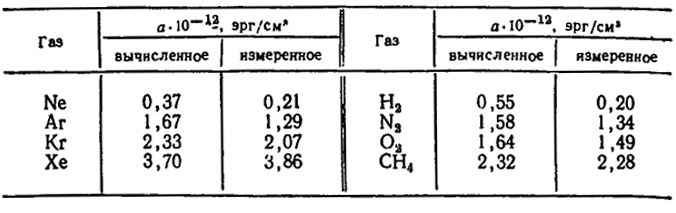
В табл. XXIII.3 сравниваются вычисленные (Слетером и Кирквудом) и наблюдаемые значения постоянной а в уравнении Ван-дер-Ваальса:
(p +
)(υ-
b) =
RT.
Промежуточной между молекулярными и химическими силами служит так называемая водородная связь. В ряде случаев атом водорода связывается не с одним атомом, как это отвечало бы его валентности, а с двумя.
Таблица XXIII.3. Сравнение вычисленных и измеренных значений постоянной Ван-дер-Ваальса
626
Наиболее типичным проявлением водородной связи является ассоциация карбоновых кислот. На рис. XXIII.8 показана структура димера муравьиной кислоты. - Мы видим, что прочность димера (энергия диссоциации 59,5 кДж) определяется двумя водородными связями, осуществляемыми
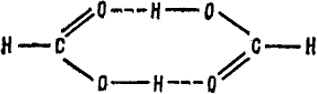
Рис. XXIII.8. Ассоциация молекул кислот
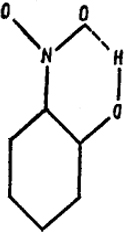
Рис. XXIII.9. Внутренняя водородная связь
каждым атомом водорода с кислородом "чужой" молекулы. Энергия одной водородной связи обычно колеблется между 21-38 кДж/моль. Водород способен давать водородную связь с кислородом, азотом и галоидами. Так называемая "внутренняя водородная связь" определяет строение многих молекул. На рис. XXIII.9 показан типичный случай такой связи в молекуле ортонитрофенола, при которой образуется второе кольцо.
Водородная связь определяет диссоциацию полимера фтористого водорода. Энергия диссоциации, например, H6F6 составляет 166 кДж/моль, т.е. 27,5 кДж/моль на одну водородную связь.
Большую роль играет водородная связь в прочности ряда кристаллических тел. Так, твердая борная кислота состоит из слоев молекул В(ОН)3. Эти молекулы связаны водородными связями. Существенную роль водородная связь играет в кристаллах диаспора (АlНО2) и лепидорита FeO(OH), обеспечивая связь между соседними атомами кислорода.
Особенно велика роль водородной связи в структуре льда и воды. Малая плотность льда связана с малым числом соседей у атома кислорода (4 атома водорода). Это оказывается все же выгодным благодаря выигрышу энергии
627
при образовании водородных связей. Приблизительно 3/4 теплоты сублимации льда обязано водородным связям.
Водородная связь играет большую роль в биологических процессах. Она определяет многие свойства высокополимеров. Так, потеря свободного вращения и, следовательно, гибкости (см. гл. XIII) часто связана с мостиками водородной связи.
Природа водородной связи полностью не выяснена. То обстоятельство, что водород дает ее с электроотрицательными атомами, делает вероятным существенную роль электростатического взаимодействия. Маленький, положительно заряженный ион водорода способен дать значительную энергию связи с соседними отрицательными ионами. Координационное число два может определяться геометрическими обстоятельствами (больше двух атомов не могут приблизиться к малому катиону водорода).
Имеются, однако, указания на то, что наряду с электростатическим притяжением в водородной связи играет роль электронное взаимодействие, связанное с образованием орбит, охватывающих атом водорода и соседние атомы.
628
