Все рассмотренное выше относилось к квантовой трактовке отдельных связей и, следовательно, велось в рамках структурных химических формул.
Наиболее простую концепцию, связанную со структурными формулами, представляет аддитивная схема, по которой свойства молекул определяются свойствами представленных в ней связей. При этом свойство связи сохраняется постоянным во всех соединениях.
В большей части опыта аддитивная схема выполняется хорошо. Это относится к теплотам сгорания (т.е. энергии связей), расстоянию между атомами, молекулярной рефракцией, реакционной способности и многому другому. Так, например, в очень большом числе органических соединений расстояние между атомами для С–С-связей равно 0,154 нм, а для С = С 0,132 нм.
Однако химический опыт указывал на ограничение применения аддитивной схемы. Впервые это было сформулировано В.В. Марковниковым и А.М. Бутлеровым. Они установили ряд фактов влияния связей друг на друга, выходящих за упрощенные представления аддитивной схемы. Особенно убедительным случаем невыполнения этой схемы являются ароматические соединения.
Действительно, в рамках структурных представлений бензол должен содержать три двойные и три одинарные связи между атомами углерода. Однако, как показывают методы исследования, расстояния между соседними атомами углерода в бензоле одинаковы и равны 0,140 нм, т.е. не отвечают ни двойной, ни одинарной связи. Вообще весь химический эксперимент и все физические методы исследования показывают, что бензол обладает большей симметрией, чем это следует из химической формулы. В соответствии е химической структурой формулы следовало ожидать наличия двух изомеров у ортодихлорбензола, что не подтверждается опытом. Химики пытались описать строение бензола и других подобных соединений, не укладывающихся в рамки языка структурных формул, путем некоторого развития языка валентности. Так, Кекуле ввел понятие осцилляции валентности (одинарная и двойная связи непрерывно меняются местами). Некоторые авторы ввели представление о дроблении валентности, полуторных связях и др.
Квантовая механика дала основание для нескольких приближенных трактовок ароматических и других подобных молекул. Мы остановимся на двух из них.
610
В теории резонанса (Л. Поллинга) молекула описывается квантово-механической суперпозицией нескольких структур. Так, собственная функция электронов бензола 6р-электронов, расположенных перпендикулярно плоскости кольца) описывается как линейная комбинация пяти функций, отвечающих пяти изображенным на рис. XXIII.3 структурам. Можно показать, что они представляют собой полный набор независимых структур.
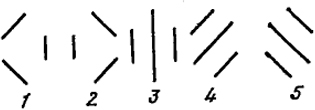
Рис. XXII 1.3. Связи π-электронов в бензоле
В основном состоянии, как показывает расчет, собственная функция л-электронов бензола представляется следующим образом:
ψ = N[ψ1 + ψ2 + 0,2(ψ3 + ψ4 + ψ5)],
где N - нормирующий фактор.
Энергия молекулы, описываемой линейной комбинацией структур, всегда ниже, чем энергия любой из этих структур. Это следует из вариационного принципа квантовой механики (см. гл. XXII).
Действительно, так как система "выбирает" коэффициенты в линейной комбинации функций таким образом, чтобы энергия была минимальна, привлечение нескольких состояний всегда снижает энергию. Поэтому соединения, в которых существует резонанс состояний, не укладываются в схему аддитивности энергии. Из отклонения величины энергии (например, теплоты сгорания) от аддитивности можно вычислить значение обменного интеграла между соседними р-электронами, определяющего величину энергии электронов ароматических соединений.
Таким образом, резонанс не явление, а приближенное описание состояния электронов молекул.
Согласно идее Л. Поллинга, на основе измерения неаддитивности какого-либо свойства молекулы (например, размера связи, теплоты сгорания, спектра, рефракции и др.) можно определить веса различных структур, а затем предсказать неаддитивность любого другого свойства. Так, Л. Поллинг ввел понятие о двоесвязности связей (доля участия двойной связи). В этане связь С–С на 100 % одинарная, в этилене - на 100 % двойная, в бензоле - на 50 %
611
одинарная, на 50 % двойная. На основе этих и других привлекаемых соединений (например, графита) строится полуэмпирический график двоесвязность - расстояние между атомами, который позволяет потом по расстоянию определять двоесвязность любых молекул и, следовательно, их реакционную способность.
Следует отметить, что развитая в Англии теория мезомерии весьма близка к теории резонанса, хотя опирается в основном на химический материал и не привлекает квантово-химические расчеты и физические свойства молекул.
Теория резонанса стремится описать соединения, выходящие за рамки структурной теории на основе ее образов и представлений. Очевидно, однако, что можно принять для бензола, что р-электроны не образуют пар, а все двигаются вокруг шестичленного кольца, как двигаются π-электроны в графите, определяя его металлическую проводимость.
Такой не связанный с обычной валентной схемой.подход к электронам молекул осуществлен и теории молекулярных орбит (Гунд, Мулликен, Герцберг). По этой теории электроны не образуют пар, локализованных между двумя атомами, а имеют молекулярные орбиты, охватывающие все атомы.
Отличие двух рассматриваемых приближений описания молекул проще всего проследить на примере молекулы водорода.
Мы рассмотрели (§ 3) собственную функцию такой молекулы с точки зрения теории электронных пар (метод валентных связей). Она выражалась для основного состояния следующим образом:
ψ = C[ψA(1)ψB(2) + ψB(1)ψA(2)].
(XXIII.14)
При описании молекулы водорода по теории молекулярных орбит мы должны поступать аналогично тому, как мы строили функции атомов при обсуждении периодической системы. Будем, как и всегда, "одевать" электронами "голые", локализованные в определенных местах пространства ядра, занимая поочередно различные состояния, учитывая их энергии и выполняя запрет Паули. Роль водородных функций будут играть функции, описывающие состояние электронов в H
.
В молекуле водорода два электрона могут занять орбиту, описываемую функцией (XXII.6). При этом их спины, в соответствии с принципом Паули, должны быть антипараллельны.
Таким образом, молекула водорода будет описываться
612
так:
ψ = C[ψA(1) + ψB(1)][ψA(2) + ψB(2)].
(XXIII.15)
Приняв общую функцию равной произведению множителей, описывающих отдельные электроны, мы полагаем приближенно их движение независимым друг от друга.
После перемножения скобок в уравнении (XXIII. 15) получим,
ψ = С[ψA(1)ψB(2) + ψB(1)ψA(2) + ψA(1)ψA(2) + ψB(1)ψB(2)].
(XXIII.16)
Первые два члена в уравнении (XXIII.16) совпадают с уравнением (XXIII.14). Третий и четвертый члены описывают ионные состояния, в которых оба электрона находятся либо у первого атома (A-B+), либо у второго (A+B-).
Таким образом, в методе валентных связей ионные состояния не учитываются вообще, а в теории молекулярных орбит их вес принимается одинаковым и равным весу гомеополярного состояния. Конечно, обе концепции являются некоторыми грубыми приближениями, имеющими определенные области целесообразного применения. В частности, молекула водорода количественно лучше описывается теорией спин-валентности. Теория молекулярных орбит, как и теория спин-валентности, объясняет отсутствие химического взаимодействия у атомов гелия и свойства насыщаемости валентности.
Действительно, в молекуле He2 надо разместить четыре электрона. Первые два мы можем поместить на первую молекулярную орбиту, которая была занята двумя электронами в молекуле водорода. Однако вторые два электрона мы должны поместить на орбиту ψ-. Мы знаем, что эти два электрона не дают связи, а отталкиваются (разрыхляющиеся электроны). При этом обменная часть энергии связи (+β) точно равняется обменной части энергии отталкивания (-β). Таким образом, по теории молекулярных орбит, обменная энергия у двух взаимодействующих атомов гелия равна нулю. Следовательно, метод молекулярных орбит приводит к отсутствию взаимодействия у атомов с насыщенными оболочками, в то время как теория спин-валентности более точно описывает отталкивание их.
Очень грубой оценкой энергии связи молекул может служить разница числа связывающих и разрыхляющих электронов. Так, энергия диссоциации молекулы H2 приблизительно вдвое больше энергии диссоциации Не
. Для того,
613
чтобы строить "периодическую систему" гомоядерных молекул, т.е. "одевать" постепенно ядра орбитами, следует расположить возможные молекулярные орбиты по энергиям. В обозначении орбит следует отразить "генетические" характеристики, т.е. атомные орбиты, в которые переходят молекулярные при диссоциации, величину λ, а также поведение функции, описывающей молекулярные орбиты при отражении в центре симметрии (четные и нечетные функции).
Например, запись σg2s означает, что молекулярная орбита возникла из-за наложения атомных орбит 2s, λ = 0 и функция четная, т.е. не меняющая знак при отражении в центре симметрии, а πu2p отвечает λ = 1 и нечетной функция.
Уравнения энергии определяются степенью перекрывания орбит. Положительному знаку при суммировании собственных функций орбит отвечает большое перекрывание и они обладают более низкой энергией. Однако в случае р-электронов положительному знаку будет отвечать нечетная функция, так как f(rA)x + f(rB)x меняет знак при отражении в центре симметрии. В соответствии с этим расположение орбит по энергиям характеризуется следующим, образом:
σg1s < σu1s < σg2s < σu2s < πu2p < σg2p < πg2p < σu2p.
Основные состояния гомоядерных двухатомных молекул представлены в табл. XXIII.1.
Описание молекул с нелокализованными связями на основе метода молекулярных орбит не уступает проводимому на основе метода валентных связей. Для описания собственных функций электронов, охватывающих несколько атомов, используется нулевое приближение теории возмущения, подобно тому, как это выше сделано при рассмотрении иона молекулы водорода. Однако число слагаемых в функции будет равняться не двум, как это имело место в этой задаче, а будет равно числу атомов, которые охватывает общая молекулярная орбита. Так, л-электроны бензола охватывают шесть атомных орбит. Поэтому собственные функции таких молекулярных орбит будут иметь шесть слагаемых:
 (XXIII.17)
(XXIII.17)
После проведения операций, которые выполнялись для
614
Таблица XXIII.1. Энергия диссоциации двухатомных молекул

задачи иона молекулы водорода, получают систему шести линейных уравнений для определения шести коэффициентов Ci, подобных уравнению (XXIII.4). В соответствии с этим для определения энергии электронов получается уравнение не второй, а шестой степени.
Если учитывать лишь резонансные интегралы соседних атомов и, пренебрегая кулоновским взаимодействием, считать функции для разных атомов ортогональными и ввести обозначение Х = U/β, то получают следующее уравнение для определения X и, следовательно, энергии электронов:
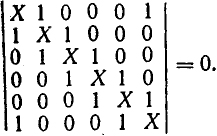
Решения этого уравнения соответственно составят: +2β; β; β; -2β; -β; -β.
π-Электроны в основном состоянии бензола займут соответственно принципу Паули три состояния с наименьшей энергией - 2β; β; β. Таким образом, общая энергия π-электронов будет равна 2·2β + 2β + 2β = 8β.
615
Таблица XXIII.2. Сравнение опытных и расчетных значении энергии резонанса

При локализации π-электронов на трех связях энергия будет равняться 3·β2β = 6β, так как энергия электрона на одной связи равна β. Таким образом, энергия резонанса равна 8β - 6β = 2β. Для сравнения теории и опыта целесообразно такие расчеты провести для разных молекул и определить энергии разонанса через β. Тогда из сопоставления этой величины с опытной энергией резонанса можно рассчитать значение β. Постоянство этой величины для разных ароматических молекул может быть критерием правильности теории.
В табл. XXIII.2 собраны соответствующие величины.
Постоянство р оказывается вполне удовлетворительным. Аналогичные расчеты делались по методу валентных связей. При этом теоретическая величина энергии резонанса естественно выражалась через обменный интеграл А. Последние два столбца таблицы показывают также постоянство А для различных соединений. Естественно, что величина А приблизительно вдвое больше β, так как она описывает энергии двух электронов. Решение системы линейных уравнений (XXIII.17) позволяет определить коэффициенты Ci. Эти коэффициенты определяют доли участия π-связей в каждой связи и, следовательно, позволяют рассчитать расстояния между атомами в данном валентном штрихе, т.е. так называемую длину связи.
Коэффициенты Сi- характеризуют степень ненасыщенности и, следовательно, реакционную способность атомов, а также заряды атомов в молекуле, т.е. полярность.
Ряд неорганических соединений совершенно не укладывается в рамки теории спин-валентности, хотя удовлетворительно описывается теорией молекулярных орбит. Это прежде
616
всего относится к молекулам с нечетным числом валентных электронов (например, NO) и к молекулам, имеющим ненасыщенные спины (например, к молекуле O2).
Для многих молекул (Сl2, NO, HCl и др.) возбуждение электрона приводит к увеличению энергии диссоциации, т.е. к увеличению энергии связи. Это обстоятельство, противоречащее теории спин-валентности, просто укладывается в теорию молекулярных орбит, если принять, что удаляется разрыхляющий электрон.
Структурные формулы в основном возникли в органической химии и хорошо описывают органические молекулы. Для неорганических молекул штрих хуже передает многообразие атомного взаимодействия. В молекуле СО существует так называемая семиполярная связь. Атом кислорода передает электрон углероду, после чего электронные оболочки обоих атомов делаются подобными электронным оболочкам азота. Поэтому Л. Полинг описывает оксид углерода формулой C- ≡≡ O+. Связь в молекуле Не
трактуется как трехэлектронная, возникающая в результате обмена места электрона иона гелия с электронной парой гелия. Высказывалось предположение, что подобная связь имеется и в О
2.
Валентный штрих не может передать всех этих различных типов взаимодействий. Помимо этого, представления о чисто ионной и чисто гомеополярной связи являются предельными. Реальные связи всегда промежуточные. Возникает вопрос об описании ионности связи.
617
