§ 5. Зависимость энергий Гельмгольца и Гиббса от параметров состояния

Найдем выражения для функций А и G одного моля идеального газа. Из определения теплоемкости при постоянном объеме следует, что

U = U₀ +

T

∫

0

  C_VdT,

где U₀ - внутренняя энергия тела при абсолютном нуле. Подставляя это выражение, а также величину S из уравнения (II.19) в уравнение A = U - TS, найдем

A = U₀ +

Е

∫

0

  C_VdT - T(C_VlnT + RlnV + C) = D(T) - RTlnV, (II.26)

где D(T) = U₀ +

T

∫

0

  C_VdT + TC_VlnT - CT - постоянная величина, зависящая только от температуры. Заменяя V отношением RT/p, получим эквивалентное выражение:

A = A⁰ + RTlnp, (II.27)

где A⁰ = D(T) - RTlnRT

50

Так как G = A + pV, то для моля идеального газа G = A + RT. Вводя RT в уравнение (II.27), находим, что

G = G⁰ + RTlnp, (II.28)

где G⁰ = A⁰ + RT;

величины А⁰ и G⁰ соответствуют значениям этих функций при р = 1.

Уравнение (II.28) позволяет, например, определить, как изменяется энергия Гиббса идеального газа при изменении давления.

Определим, насколько величина G₂ одного моля идеального газа при 10⁸ Па (1000 атм) и 300 К больше, чем G₁ при 10⁵ Па (1 атм):

G₁ = G⁰(300) + R300ln10⁵;
G₂ = G⁰(300) + R300ln10⁸;

Искомая разность ΔG = G₂ - G₁ = R 300 ln 1000.

Это увеличение свободной энергии Гиббса равно работе обратимого изотермического сжатия газа от p₁ = 10⁵ до р₂ - = 10₈ Па, т.е.

ΔG = RT ln (p₂/p₁) = R 300 ln 10³ = 17230 Дж.

Функции А и G широко используются для анализа возможности различных процессов и реакций. Пусть, например, мы хотим выяснить, возможно ли превращение графита в алмаз при данных температуре и давлении. Если в этих условиях энергия Гиббса алмаза. G_a больше, чем графита, G_гр и AG положительны, то такой процесс невозможен. Однако при других значениях р и Т знак величины может измениться на обратный. Действительно, в настоящее время этот процесс осуществляется при температурах порядка 3000 К и давлениях 10¹⁰ Па.

Для решения большого числа подобных задач необходимо знать зависимость функции А и G от температуры, объема и давления.

Продифференцировав уравнение A = U - TS:

dA = dU - TdS - SdT

и подставив в него значение TdS = δQ = dU + pdV, получим:

dА = -pdV - SdT. (II.29)

Это уравнение дает зависимость А от объема и температуры.

51

Из него также следует, что

(∂А/∂V)_т = -р; (II.30) (∂А/∂T)_V = -S; (II.31)

Дифференцируя уравнение G = U - TS + pV, получим: dG = dU - TdS - SdT + pdV + Vdp.

Подставляя в это уравнение значение TdS = dU + pdV, найдем зависимость энергии Гиббса от давления и температуры:

dG = Vdp - SdT, (II.32)

из которой следует, что

(∂G/∂р)Т = V (II.33) (∂G/∂Т)_р = -S. (II.34)

Подставляя значения S из уравнений (II.31) и (II.34) в выражения для А и G, получим два важных уравнения:

А = U + Т(∂А/∂T)_V (II.35) G = H + T(∂G/∂T)_p (II.36)

зависимостей этих функций от температуры для однородного вещества. Эти зависимости можно представить в более удобном виде. Если, например, разделить обе части уравнения (II.36) на Т₂, то

(II.37)

или

d(G/T)_p = Hd(1/T). (II.38)

Уравнения (II.35) и (II.36) называются уравнениями Гиббса-Гельмгольца.

Для осуществления соответствующих вычислений при помощи этих уравнений необходимо знание теплоемкостей C_V и С_p.

Уравнения (II.35) - (II.37) для изменений функций А и G, т.е. для процессов, принимают вид:

ΔA = ΔU + Т (∂ΔA/∂T)_V; (II.39) ΔG = ΔH + T(∂ΔG/∂T)_p; (II.40) [∂(ΔG/T)/∂T]_p = - ΔH/T². (II.41)

Из уравнений (II.30) - (II.34) вытекают важные соотношения

52

для зависимости энтропии от объема и давления. Продифференцируем уравнение (II.30) по температуре, а уравнение (II.31) - по объему:

∂²A/∂V∂T = - (∂_p/∂T)_V; ∂²A/∂T∂V = - (∂S/∂V)_T.

Так как А - функция состояния, то величина второй производной не зависит от порядка дифференцирования и, следовательно:

(∂S/∂V)_T = (∂p/∂Т)_V. (II.42)

Дифференцируя уравнение (II.33) по температуре, а уравнение (II.34) по давлению, найдем:

∂²G/∂p∂T = (∂V/∂T)_p и ∂²G/∂T∂p = - (∂S/∂p)_T.

Так как G так же, как и А, функция состояния, то

(∂S/∂p)_T = - (∂V/∂T)_p. (II.43)

Из уравнения dS = δQ/T следует¹, что

(∂S/∂T)_V = C_V/T; (II.44) (∂S/∂T)_p = C_p/T. (II.45)

Из уравнения (II.15) следует выражение для дифференциала внутренней энергии:

dU = TdS - pdV (II.46)

и для ее частных производных:

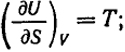(II.47) 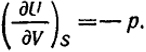(II.48)

Из определения энтальпии H = U + pV и уравнения (II.46) следует, что

dН = TdS + Vdp (II.49)

и соответственно

(II.50) 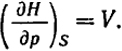(II.51)

Существенно, что уравнения (II.29), (II.32), (II.46) и (II.49) справедливы для систем с постоянным количеством

53

вещества, т.е. для закрытых систем. В открытых системах, когда изменяются количества веществ, при поступлении извне или при удалении, а также вследствие химических реакций, соответственно будут изменяться и их термодинамические свойства. Например, внутренняя энергия открытой системы зависит от числа молей входящих в нее компонентов n₁, n₂, ...n_i. Так как дифференциал внутренней энергии является полным, то

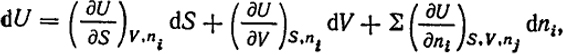(II.52)

где индекс n_i - означает, что при дифференцировании число всех компонентов n_i остается постоянным, а индекс n_j показывает, что постоянны все п, кроме n_i, т.е. числа молей компонента, по которому производится дифференцирование (j ≠ i). Производная

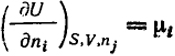(II.53)

называется химическим потенциалом. С учетом уравнений (II.47), (II.48) и (II.53) выражение (II.52) принимает вид:

dU = TdS - pdV + Σμ_idn_i. (II.54)

Поочередно, подставляя дифференциал dU из уже приводившихся уравнений (dH = dU + pdV; dA - dU - TvdS - SdT и G = dU - TdS - SdT + pdV + Vdp) в уравнение (II.54) получим три соотношения:

dH = TdS + Vdp + Σμ_idn_i; (II.55) dA = -SdT - pdV + Σμ_idn_i; (II.56) dG = -SdV + Vdp + Σμ_idn_i. (II.57)

Таким образом, из уравнений (II.54) - (II.57) следует, что

(II.58)

Особенно важным является выражение, связывающее химический потенциал с энергией Гиббса: μ_i = (

∂G

∂ni

)_T,p,nj. Эта величина характеризует изменение энергии Гиббса системы при бесконечно малом изменении количества вещества i при постоянных температуре, давлении и количествах остальных веществ в этой системе в расчете на один

54

моль. Отсюда следует, что химический потенциал чистого вещества равен энергии Гиббса одного моля вещества:

μ_i = G_i (II.59)

Химический потенциал - понятие, аналогичное температуре и давлению. Разница температур определяет направление передачи тепла от одного тела к другому, а разница давлений - перенос вещества. В следующих главах будет показано, что разность величин ц,- определяет направление химических реакций, фазовых превращений, диффузии веществ из одной фазы в другую.

55

---