§ 4. Насыщаемость связи

Как указывалось выше, насыщаемость - наиболее характерная черта сил химического взаимодействия. Поэтому уже в первой работе В. Гайтлер и Ф. Лондон показали, что, в частности, атом гелия не способен к образованию связи с другими атомами.

Вообще можно показать, что энергия взаимодействия между электроном, входящим в электронную пару, и любым другим электроном определяется величиной Q - (A/2), где Q - энергия кулоновского взаимодействия, а А - обменный интеграл, как и в формуле (XXIII.10). Так как А имеет отрицательный знак, то электрон, входящий в пару, отталкивается от любого третьего электрона. Смысл и величина этого отталкивания могут быть понятны на основе следующего рассуждения. Входящий в пару электрон все время меняется направлением спина со своим соседом, поэтому с третьим электроном он также имеет как параллельное, так и антипараллельное расположение спинов в зависимости от вероятностей этих состояний.

Выше указывалось, что вероятность параллельного расположения спинов (при которой энергия взаимодействия с третьим электроном равна Q - А) в три раза больше антипараллельного (с энергией Q + A).

Таким образом, результирующая энергия взаимодействия электрона пары с третьим электроном

1/4(Q + A) + 3/4(Q - A) = Q - (A/2). (XXIII.11)

Таким образом, между атомами (или молекулами) с замкнутыми оболочками имеет место отталкивание. Это отталкивание и определяет радиусы систем с замкнутыми оболочками.

В § 2 было принято, что зависимость энергии этого отталкивания от расстояния описывается степенной функцией. Квантово-механические расчеты показали, что лучшим приближением по сравнению со степенной функцией является более сложная функция.

Отталкивание насыщенных молекул точно так же, как и отталкивание атома от насыщенной молекулы, приводит к появлению энергии активации. Рассмотрим этот вопрос несколько подробнее для случая взаимодействия атома B₁ с молекулой В₂В₃ с образованием молекулы B₁B₂ и свободного атома В₃.

Квантово-механический расчет приводит к следующей

603

формуле для энергии взаимодействия трех атомов:

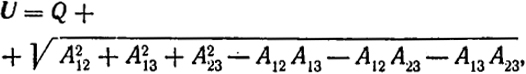(XXIII.12)

где Q - кулоновская энергия; A_ik- обменный интеграл между двумя атомами B_i и B_k.

Если расстояние первого атома (B₁) от первых двух велико, то, так как A₁₂ = A₁₃ = 0, формула (XXIII.12) переходит в формулу (XXIII.10):

U = Q + A₂₃.

При приближении первого атома к молекуле В₂В₃ имеет место отталкивание его от молекулы. Для больших расстояний атома от молекулы можно считать, что А₁₂ и А₁₃ значительно меньше A₂₃. Пренебрегая квадратом этих малых величин, получим

U = Q + A₂₃ - (A₁₃/2) - (A₁₂/2).

Эта формула находится в соответствии с формулой (XXIII.11). Атом B₁ отталкивается от обоих электронов пары молекул В₂В₃. Энергия активации нужна для преодоления этого отталкивания.

По мере приближения атома B₁ расстояние В₂В₃ увеличивается. Энергия системы в соответствии с формулой (XXIII.12) и путь реакции показаны на рис. XVI.6. Мы ограничимся здесь простейшей, данной Ф. Лондоном, оценкой энергии активации. Пусть атом B₁ приближается к молекуле В₂В₃ по линии связи со стороны В₂. Тогда расстояние B₁B₃ существенно больше В₁В₂. Поэтому будем полагать /4i3 = 0. Тогда

U = Q + √A

2

12

  + A

2

23

  - A₁₂A₂₃. (XXIII.13)

Примем в этой приближенной оценке, что расстояние В₂В₃ постоянно. Тогда U зависит от расстояния В₁В₂. Пренебрежем, кроме того, кулоновской энергией Q. Тогда U меняется лишь потому, что с расстоянием В₁В₂ меняется A₁₂. Чтобы найти максимальное значение энергии системы энергию переходного состояния), необходимо приравнять нулю ∂U/∂A₁₂ при A₂₃ = const:

Отсюда A₁₂ = A₂₃/2.

604

Подставив эту величину в уравнение (XXIII. 13), получим

U = Q + (√3/2)A = Q + 0,85A.

Таким образом, энергия рассматриваемой конфигурации изменилась от значения А (расстояние В₁В₂ равно бесконечности) до значения 0,85 А (переходное состояние). Отсюда следует, что энергия активации составляет около 15 % от энергии связи. Результат этого приближенного расчета близок к результатам точного расчета по формуле ;(ХХIII.12) (см. рис. XVI.6).

605