§ 3. Гомеополярная связь

Гомеополярная связь обязана специфическому квантово-механическому эффекту. Весьма поучительна ошибка, допущенная в первых работах, посвященных квантово-механическому

594

толкованию гомеополярной связи. Мы разберем ее на примере простейших гомеополярных молекул - молекул водорода Н₂ и иона молекулы водорода Н

+

2

  .

Целью квантово-механического рассмотрения этих двух систем является прежде всего выяснение природы их прочности. При образовании молекул водорода из атомов выделяется более 418 кДж/моль, а при образовании иона молекулы водорода из атома водорода и иона водорода - около 240 кДж/моль.

Важно показать специфические особенности гомеополярной связи и прежде всего свойства насыщаемости. Силы, приводящие к образованию молекулы водорода, должны отсутствовать в случае взаимодействия двух атомов благородных газов и приводить к отталкиванию третьего атома водорода от молекулы водорода.

В первых исследованиях квантовая механика была использована лишь для описания электронного облака взаимодействующих атомов. Само же взаимодействие описывалось на основе законов электростатики.

Рассмотрим, к чему должно приводить такое взаимодействие в системах атом водорода - ион водорода и атом водорода - атом водорода. Для этого выясним характер электростатического поля, действующего внутри электронного облака атома. Очевидно, что на бесконечно большом расстоянии от ядра напряженность этого поля равна нулю, так как атом в целом нейтрален и электроны полностью экранируют ядро. Однако на некотором конечном расстоянии ядра r заряд ядра экранирован лишь долей электронов, которые находятся на расстоянии, меньшем r, так как притяжение, создаваемое остальной частью электронов внутри сферы, равно нулю.

Следовательно, внутри нейтрального атома во всех точках напряженность отвечает действию положительного заряда. Отсюда следует, что проникновение положительного заряда внутрь атома всегда будет вызывать отталкивание. Таким образом, электростатическое взаимодействие приводит к отталкиванию иона водорода от атома водорода и никак не может объяснить значительную прочность иона молекулы водорода. При приближении двух нейтральных атомов происходит наложение электронных облаков. Так как при этом отрицательный заряд оказывается внутри поля положительных зарядов, то возникает притяжение, которое действует, пока расстояние между атомами не окажется слишком малым. При этом положительное ядро будет

595

проникать внутрь этого поля, что должно в конце концов привести к отталкиванию.

Таким образом, электростатическое притяжение нейтральных атомов должно характеризоваться наличием равновесного расстояния, при котором энергия системы будет минимальной. Однако это притяжение нейтральных атомов не может иметь существенного значения для объяснения химического взаимодействия. Прежде всего электростатическое притяжение должно существовать между двумя любыми нейтральными атомами, в том числе и атомами благородных газов. Кроме того, к двум приблизившимся атомам должны притягиваться третий и четвертый. Таким образом, электростатическое притяжение нейтральных атомов не обладает свойством насыщенности.

Наконец, количественный расчет электростатического взаимодействия двух атомов водорода показал, что величина этой энергии составляет лишь около 10 % энергии связи.

Химическая связь не может быть, следовательно, истолкована как результат электростатического притяжения атомов. Она возникает вследствие того, что при приближении атомов меняется вид электронного облака, так как электроны с атомных "орбит" переходят на охватывающие все ядра "молекулярные орбиты".

Этот переход вызван особым квантово-механическим эффектом, который определяется линейностью уравнения Шредингера. Известно, что для линейного дифференциального уравнения общие решения ψ представляют линейную, комбинацию частных решений ψ₁, ψ₂, ψ₃ и т.д.

ψ = C₁ψ₁ + C₂ψ₂ + ... + ∑C_iψ_i (XXIII.4)

Пусть все частные функции образуют ортонормированную систему

∫ψ_iψ_jdτ = 0; ∫ψ_iψ_idτ = 1.

Построим функцию, сопряженную функции ψ

ψ = C₁ψ₁ + C₂ψ₂ + ... .

Условие нормировки записывается следующим образом:

∫ψψdτ = 1.

Отсюда ∑C_iC_i = 1.

Таким образом, сумма квадратов модулей - коэффициентов должна равняться единице, т.е.

∑∣C_i|² = 1. (ХХIII.5)

596

Следовательно, ∣C_i|² определяет долю, вносимую i-тым состоянием в общее.

При взаимодействии атомов всегда осуществляется суперпозиция различных состояний.

Рассмотрим простейшую молекулярную систему - молекулу Н

+

2

  , т.е. два ядра водорода (A и В) и один электрон. Очевидно, что существуют два состояния с совершенно одинаковой энергией. В первом электрон находится у ядра А, а во втором - у ядра В:

ψ₁ = ψ_A(1); ψ₂ = ψ_B(1),

где ψ_A и ψ_B - функции, описывающие атом водорода в основном состоянии.

Как было показано в гл. XXII,

ψ_A = Ne-r_A(1)/r₀.

Согласно уравнению (XXIII.4):

ψ = C₁ψ_A(1) + C₂ψ_B(1).

Из соображений симметрии следует, что доля, вносимая каждым из состояний, должна быть одинакова. Другими словами, C

2

1

  = C

2

2

  . Следовательно, C₁ = ±C₂.

Таким образом, в результате суперпозиции первого и второго состояний возникают два состояния:

ψ₊ = C₁[ψ_A(1) + ψ_B(1)]; ψ_- = C₁[ψ_A(1) - ψ_B(1)]. (XXIII.6)

В этих состояниях вид электронного облака совершенно иной, чем в первом и втором. Для анализа характера электронного распределения рассмотрим квадрат функции:

ψ

2

±

  = C

2

1

  [ψ

2

A

  (1) + ψ

2

B

  (1) ± 2ψ_A(1)ψ_B(1)].

В состояниях, возникших в результате суперпозиции указанных состояний, наряду с ψ

2

A

  (1) и ψ

2

B

  (1), описывающими эти состояния, возникает член 2ψ_A(1)ψ_B(1). Функции ψ

2

A

  (l) и ψ

2

B

  (1) обладают сферической симметрией, а ψ_A(1)ψ_B(1) = N²e

rA(1) + B(1)

r0

  имеют ось симметрии АВ. При этом поверхностями одинаковой плотности являются эллипсоиды вращения. Действительно, ψ_A(1)ψ_B(1) постоянно в точках, где постоянная сумма r_A + r_B.

Таким образом, ψ_A(1)ψB(1) представляет собой охватывающее оба ядра молекулярное облако. В этом облаке электронная плотность велика на плоскости, перпендикулярной

597

оси молекулы и проходящей через середину расстояния между ядрами. Электрон, находясь между ядрами, притягивается к ним, чем и определяется прочность молекулы. В состоянии ψ₊ член, описывающий это охватывающее облако, входит со знаком "плюс", а в состоянии ψ_- он вычитается. В результате функции ψ_- (и ее квадрат) равны нулю на рассмотренной выше плоскости. Очевидно, что в состоянии ψ⁺ молекула Н

+

2

  должна быть устойчива, а в состоянии ψ_- должно иметь место отталкивание между водородом и ионами водорода.

Мы определили волновую функцию иона молекулы водорода, исходя из соображений симметрии. Рассмотрим более общий метод определения волновых функций и энергий атомных систем в так называемом нулевом приближении теории возмущений. Эта теория применяется для определения изменения функций и энергий под влиянием какого-либо малого возмущающего фактора. Уравнение Шредингеpa (XX.8) может быть переписано следующим образом:

H_ψ = _Eψ, (XXIII.7)

где Н - оператор, включающий операции умножения и дифференцирования: H = -(h²/8πm)Δ + U. Представим себе, что нам известно решение ψ₀ для некоторого оператора H₀: H₀ψ₀ = E₀ψ₀. Пусть, однако, на частицу дополнительно воздействует возмущающее поле h. Мы должны, следовательно, искать решение уравнения (H₀ + h)ψ = Eψ. Умножив обе части этого уравнения на ψ и проинтегрировав, получим, учитывая нормировку функции ψ:

E = ∫ψH₀ψdτ + ∫hψdτ.

Нулевое приближение теории возмущения заключается в том, что мы оцениваем энергию, полагая, что функция не изменилась под влиянием возмущения. Заменив ψ на ψ₀ в предыдущем выражении, получим

E = ∫ψ₀H₀ψ₀dτ + ∫hψ₀ψdτ = E₀ + ∫hψ₀ψdτ.

Таким образом, зная h и решение невозмущенной задачи, можно определить энергию возмущения ∫hψ₀ψdτ.

Вопрос несколько усложняется, если в невозмущенной задаче имеется несколько решений с одинаковой энергией, как в случае взаимодействия атома водорода с протоном.

Возмущающий потенциал h определяет выбор коэффициентов C_i, с которыми возмущенные функции ψ_i входят в линейную комбинацию, образующую общую волновую

598

функцию. Эти коэффициенты могут быть определены из требования минимума энергии. Их можно получить также следующим простым способом. Подставив выражение (XXIII.4) в (XXIII.7) для случая двух вырожденных состояний, получим

C₁(Hψ₁ - Eψ₁) + C₂(Hψ₂ - Eψ₂) = 0.

Умножая это выражение поочередно на ψ₁ и ψ₂ и интегрируя, получим

C₁(H₁₁ - E) + C₂(H₁₂ - ES) = 0;

C₁(H₂₁ - ES) + C₂(H₂₂ - E) = 0.

Здесь H_ik = ∫ψ_iHψ_kdτ, a S = ∫ψ₁ψ₂dτ - неортогональность функций ψ₁ и ψ₂.

В случае иона молекулы водорода ψ₁ = ψ_A, ψ₂ = ψ_B. Таким образом:

H₁₁ = H₂₂ = ∫ψ_A(-

h2

8π2m

  Δ -

e2

rA

  -

e2

rB

  +

e2

R

  )ψ_A,

где R - расстояние между ядрами.

Так как -

h2

8π2m

  Δψ_A -

e2

rA

  = E₀ψ_A, где E₀ - энергия атома водорода, то

H₁₁ = H₂₂ = ∫E₀ψ

2

A

  dτ - ∫

e2

rB

  ψ

2

A

  dτ +

e2

R

  ∫ψ

2

A

  dτ = E₀ + q,

где q = -e²∫

ψ 2 A

rB

  dτ +

e2

R

  представляет собой кулоновское взаимодействие атома водорода с чужим ядром. Для матричного элемента H₁₂ получим

H₁₂ = ∫ψ_B(-

h2

8π2m

  Δ -

e2

rA

  -

e2

rB

  +

e2

R

  )ψ_Adτ.

Считая, что R велико и функции ψ_A и ψ_B ортогональны, получим H₁₂ = β, где β = ∫(ψ_Aψ_B/r_A)dτ носит название резонансного интеграла.

Таким образом:

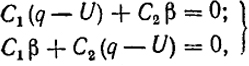(XXIII.8)

где U = E - E₀ - энергия взаимодействия. Условие существования решения однородных уравнений (XXIII.8) запишется

599

следующим образом:

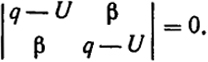
Отсюда

U_± = q±β. (XXIII.9)

Подставляя уравнение (XXIII.9) в (XXIII.8), мы убедимся, что U₊ отвечает равенство C₁ = C₂, a U_- равенство С₁ = -С₂. В расчете, подобном проведенному Унсольдом, учитывалось лишь кулоновское взаимодействие q, что приводило к отталкиванию протона от атома водорода. Устойчивость иона молекулы водорода обусловлена обменным интегралом р, описывающим взаимодействие охватывающего ядра, обладающего эллиптической симметрией, облака с протонами.

Энергия притяжения между двумя атомами водорода возникает в результате аналогичного эффекта.

Для системы, состоящей из двух атомов водорода, также существуют два состояния, относящиеся к одной энергии.

В первом состоянии электрон I находится на атомной орбите атома А, а электрон 2 - на атомной орбите атома В. Так как вероятность сложного события определяется как произведение вероятностей независимых событий, то ψ₁ = ψ_A(1)ψ_B(2).

Можно считать в нулевом приближении для случая большого расстояния между атомами, что ψ_A и ψ_B остаются водородными функциями. Очевидно, что перемена местами электронов не изменит энергии системы. Поэтому ψ₂ = ψ_A(1)ψ_B(1). Как и ранее, ψ = C₁ψ₁ + C₂ψ₂.

Из соображений симметрии мы снова должны потребовать, чтобы C

2

1

  = C

2

2

  и C₁ = ±C₂. Следовательно, ψ_± = C₁[ψ₁ ± ψ₂].

Снова, как и в случае Н

+

2

, плотность электронного облака, определяемая ψ

2

177

  , содержит наряду с двумя членами, описывающими атомные "орбиты" (ψ

222

1

  и ψ

2

2

  ), член, описывающий молекулярную орбиту (2ψ₁ψ₂).

В случае молекулы водорода ψ₁ψ₂ = ψ_A(1)ψ_A(2)ψ_B(2).

Воспользовавшись функцией для электрона атома водорода, получим: ψ₁ψ₂ = N²e^{-r_A(1) + r_B(1)/r₀}e^{-r_A(2) + r_B(2)/r₀}.

Мы видим, что оба электрона располагаются на той же охватывающей орбите, на которой находится один электрон иона молекулы водорода.

600

Если по законам квантовой механики рассчитать энергию взаимодействия двух атомов U так, как мы сделали это для иона молекулы водорода, то возникают два члена. Электростатическое взаимодействие двух атомов водорода обозначим Q, а обменное (называемое обменным интегралом) - буквой А:

U_± = Q ± A. (XXIII.10)

Как указывалось выше, кулоновское взаимодействие атомов дает притяжение, которое, однако, обеспечивает лишь около 10 % энергии химической связи. Член А содержит взаимодействие электронов, находящихся на молекулярных орбитах с ядрами и друг с другом. Он имеет отрицательный знак и, следовательно, приводит к притяжению атомов для терма U₊ и к отталкиванию для терма U_-.

На рис. XXIII.1 даны потенциальные кривые для этих термов взаимодействия двух атомов водорода, вычисленные впервые В. Гайтлером, Ф. Лондоном и И. Сигкура. Позднее был проделан квантово-химический расчет, точность которого отвечала точности спектроскопических измерений энергии диссоциации.

Следовательно, причина возникновения притяжения между двумя атомами водорода сводится к тому, что вследствие квантово-механического принципа суперпозиции электроны переходят с атомных на энергетически более выгодные молекулярные орбиты. Отталкивание, отвечающее состоянию U_- - типичное явление, имеющее весьма большое значение в атомных процессах. Именно оно определяет свойство насыщаемости связи, энергию активации, размеры молекул и др.

Таким образом, два приближающихся атома могут либо притягиваться друг к другу и образовывать молекулу, либо отталкиваться и расходиться после упругого отталкивания. Какова же вероятность этих двух событий?

601

Для ответа на этот вопрос рассмотрим, чем отличается состояние электронов в термах, описываемых функциями ψ₊ и ψ_-. Эти функции обладают различной симметрией в отношении обмена электронов местами. Функция ψ₊ не меняет при этой операции знака, функция ψ_- меняет знак на обратный. Другими словами, функция ψ₊ симметрична, а функция ψ_- антисимметрична.

В гл. XXII было показано, что, в соответствии с принципом Паули, общая функция, содержащая в качестве множителей функции, описывающие положение электронов (ψ_об), и их спины, должна быть антисимметричной. Функции ψ₊ должна отвечать антисимметричная спиновая функция, а функции ψ_- симметричная Для двух электронов возможны только два состояния спинов. Они могут быть или параллельны (т.е. иметь тождественное направление), или антипараллельны (т.е. направлены в разные стороны). Тождественное состояние спинов опишется симметричной спиновой функцией. Таким образом, в состоянии U₊ спины электронов образуют пару с общим спин-моментом, равным нулю; в состоянии U_- спины направлены в одну сторону, что приводит к спин-моменту, равному единице.

Спин-момент, равный единице, может иметь три, проекции на любой оси: +1; 0; -1. Спин-момент, равный нулю, может иметь проекцию, лишь равную нулю. Таким образом, статистический вес спин-момента, равного единице, равен 3, в то время как статистический вес нулевого спин-момента равен единице. Следовательно, вероятность образования пары в три раза меньше вероятности параллельного направления спинов. При встрече двух атомов водорода в одной четверти случаев они образуют молекулу (если, конечно, будет обеспечен отвод энергии образования), а в других атомы упруго оттолкнутся друг от друга.

В уравнениях кинетики образования молекулы при столкновении атомов должен среди других фигурировать стерический фактор, равный одной четверти.

Итак, валентному штриху отвечает пара электронов с насыщенными спинами. Этот результат сразу показывает тождественность сил взаимодействия, полученных в результате квантово-химического расчета, с силами химического сродства, детально изученными химиками. Прежде всего существенно то, что найденные в результате описанного расчета силы взаимодействия атомов водорода обладают насыщаемостью.

602