Одним из важнейших объектов квантовой механики является атом. Для простейшего атома (атома водорода) это задача движения одного электрона в поле протона.
565
Уравнение Шредингера запишется для этого случая следующим образом:
Δψ +
(
E +
)ψ = 0.
поскольку, как указывалось выше, потенциальная энергия электрона
U = -e2/r.
Перейдя к сферическим координатам, получим:
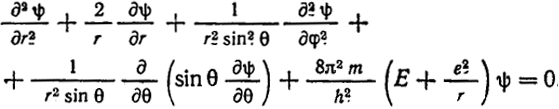 (XXII.22)
(XXII.22)
Будем искать решение в виде произведения двух функций, зависящих от расстояния между электроном и ядром г и от углов:
ψ = R(r)·T(θ, φ).
(XXII.23)
Подставив уравнение (ХХII.20) в (XXII.21) и разделив на ψ, получим:

Так как вторые два слагаемых не зависят от r, то
+
(sinθ) = -λ.
(XXII.24)
Мы видим, что Т совпадает с ранее рассмотренными функциями ротатора, так как уравнение (XXII.24) совпадает с уравнением (XXII.17). Следовательно, λ = l(l + 1) и Т = ηΦ.
Мы получим уравнение для искомой функции R:
+
+
[E +
-
]
R = 0.
(XXII.25)
Физический смысл последнего члена этого уравнения сводится к следующему. Отделив часть функции, описывающую изменение углов, т.е. вращение, мы должны получить в части функции, описывающей изменение радиуса, член, связанный с центробежной силой.
566
Известно, что эта сила равна mυ2/r. Момент вращения p = mυr (см. гл. XXII). Поэтому mυ2/r =, но р2 = (h2/4ππ2)l(l + 1).
Поэтому центробежная сила равна
.
Отсюда потенциал центробежных сил составит
∫
·
=
·
,
что совпадает с последним членом уравнения (XXII.25).
Как показывает математический анализ, решение уравнения (XXI.23) удовлетворит краевому условию R(∞) = 0 лишь в том случае, если
E = -(2π2me4)/(h2n2).
(XXII.26)
Здесь п носит название главного квантового числа, п = 1, 2, 3... При этом оказывается, что l < n.
Уравнение (XXII.26) было впервые получено Бором на основе квантовой механики Бора-Зоммерфельда.
Отметим, что в случае водородоподобного иона, в котором электрон движется вокруг ядра, обладающего зарядом Z (выраженным в величине заряда электрона), энергия возрастает в Z2 раз и вместо уравнения (XXII.26) получаем:
E = -(2π2mZ2e4)/(h9n2).
Все спектральные серии атомов водорода описываются на основе уравнения (XXII.26), если частоты линии определять по уравнению
νik = (Ei - Ek)/h.
(XXII.27)
Таким образом, всегда (для любого атома или молекулы) при переходе с одного дозволенного энергетического уровня на другой испускается один квант. Все выводы относительно квантовых чисел l и т функций сохраняются для рассматриваемого случая.
Таким образом, электрон атома водорода характеризуется тремя квантовыми числами п, l и т. При этом п меняется от 1 до ∞. Для данного значения п, l меняется от 0 до n - 1 и для заданного значения lт меняется от -l до +l.
Рассмотрим волновые функции, отвечающие п, равному 1 и 2.
567
При n = 1 l = 0. Для l = 0 T - постоянное число и ψ = R.
Решение уравнения (XXII.23) для R, отвечающее n = 1, имеет следующий вид:
R = Ne-r/r0.
(XXII.28)
Здесь
r0 = h2/(4π2me2).
(ХХII.29)
Эта величина фигурировала в теории атома Бора в качестве радиуса первой боровской орбиты.
Расчет по формуле (XXII.29) дает r0 = 0,052 нм. Нормировочный множитель N должен быть выбран таким образом, чтобы ∫R2dτ = 1.
После расчета N = π-1/2r
.
Интересно установить, на каком расстоянии от ядра расположен шаровой пояс, в котором находится максимальная по сравнению с другими шаровыми поясами вероятность найти электрон. Для решения этого вопроса необходимо найти максимум выражения R24πr2.
Расчет показывает, что радиус сферы, отвечающий наибольшей вероятности, равен r0. Таким образом, в новой теории радиус первой боровской орбиты является радиусом сферы, в которой чаще по сравнению с другими бывает электрон.
Для n = 2 и l = 0
ψ = R = N2(
- 2)e
-r/2r0.
Сфера наибольшей вероятности в этом случае находится на расстоянии, отвечающем второй боровской орбите. Для n = 2 l = 1
R = N3re-r/2r0
Угловая часть собственной функции, как и в задаче для ротатора, выразится следующим образом:
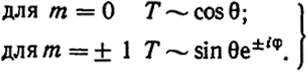
По установившейся в спектроскопии традиции электроны со значением l = 0 называются s-электроны, при l = 2 - p-электронами, при l = 2 - d-электронами и при l = 3 - f-электронами.
Мы видим, что собственные функции s-электронов зависят
568
только от r и, следовательно, обладают шаровой симметрией. Электронное облако р-электронов не зависит от угла φ (так как модуль e±iφ = l) и, следовательно, обладает осью симметрии.
Удобно преобразовать функции р-электрона, перейдя от шаровых координат к декартовым. При этом можно воспользоваться следующим обстоятельством. В отсутствие каких-либо полей энергия электрона не должна зависеть от ориентации его момента по отношению к некоторой оси. Следовательно, функции с разными значениями т принадлежат к одной энергий и подчиняются уравнению Шредингера с одним значением Е.
Если несколько функций являются решением линейного дифференциальногно уравнения, то и линейная комбинация их также является ее решением. Поэтому вместо трех функций (XXI.28), описывающих функции при l = 1, мы можем выбрать три любые линейные комбинации.
В качестве первой мы выберем функцию, отвечающую m = 0. Учитывая, что rcosθ = z, запишем ее в следующем виде:
ψ1 = F(R)z, где f(r) = Ne-r/2r0.
В качестве второй функции выберем сумму функций, отвечающих m = + 1 и m = -1.
Учитывая, что x = sin θ
мы можем написать ψ
2 =
f(
r)
x. Приняв в качестве третьей функции разницу функций, отвечающих
m = + 1 и
m = -1, мы получим третью функцию ψ
3 =
f(
r)
y. Очевидно, что эти функции обладают осями симметрии.
При заданном значении r ψ1 имеет наибольшее значение при наибольшем значении z. Поэтому эта функция представляет собой электронный тяж, вытянутый по оси z и обладающий симметрией вращения вокруг этой оси.
На плоскости ху значение функции равно нулю, так как величина z = 0. Аналогичные тяжи, но вытянутые по двум другим осям, представляют две другие функции.
На рис. XXII.5 показаны изображения электронного облака для разных значений квантовых чисел, сфотографированные со специально построенной модели. Мы видим, что облако, отвечающее s-состоянию, представляет собой некоторое шаровое облако. Облака, отвечающие р-состоянию, являются тяжами (напоминающими вращающиеся вокруг оси восьмерки), по-разному ориентированными в пространстве.
569
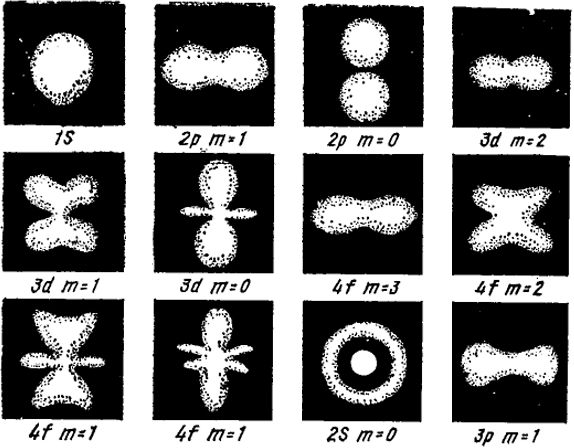
Рис. XXII.5. Изображение электронного облака атома с одним электроном
Более сложными свойствами симметрии обладают облака, соответствующие более высоким значениям азимутального квантового числа (l).
570
