§ 2. Ротатор

Пусть частица массой m вращается по шару радиусом r. Так как потенциальная энергия при вращении постоянна и может быть принята за уровень отсчета энергии, то уравнение Шредингера запишется для ротатора следующим образом:

Δψ +

8π2m

h2

  Eψ = 0. (XXII.13)

Можно перейти к шаровым координатам (r - радиус, φ - долгота, θ - широта), тогда оператор Δ выразится следующим образом:

(XXII.14)

В интересующей нас задаче искомая функция зависит от двух координат ψ - (ψ, θ). Подставляя в уравнение (XXII.12) часть оператора, зависящую от φ и θ, и умножая на r², получим:

(XXII.15)

где I = mr² - момент инерции частицы.

Будем искать решение уравнения (XXII. 13) в виде произведения функций, зависящих лишь от одного переменного.

Пусть

ψ = Φ(ψ)η(θ). (XXII.16)

Подставив уравнение (XXII.14) и (XXII.13) и разделив

563

обе части на φ, получим

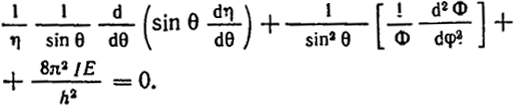(XXII.17)

Заключенное в квадратных скобках выражение должно быть постоянным для того, чтобы было выполнено разделение переменных и η не зависело от φ.

Следовательно:

1

Φ

 

d2Φ

dφ2

  = -m²,

или

d2Φ

dφ2

  = -m²Φ (XXII.18)

Решение этого уравнения запишется следующим образом:

Φ = e^imφ. (XXII.19)

Для того чтобы Φ было однозначным, т.е. выполнялось условие Φ(φ) = Φ(φ + 2π), т должно быть целым положительным или отрицательным числом. Уравнение (XXII.15) при учете равенства (XXII.16) перейдет в следующее:

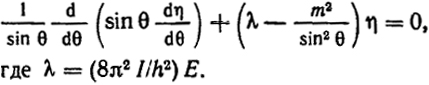(XII.20)

где λ = (8π²I/h²)Е.

Решение уравнения (XXII.18) показывает, что λ = l(l + 1), где l принимает значения 0, 1, 2, 3 ...

Следовательно:

E = (h²/8π²I)l(l + 1).

Так как энергия ротатора равняется p²/2I (см. гл. XXIII), то

p² = [h²l(l + 1)]/4π²

p = (h/2π)√l(l + 1). (XXII.21)

Таким образом, так называемое азимутальное квантовое число l имеет простой смысл. Оно представляет величины момента вращения частицы. Наименьшее значение

564

этого момента равно нулю

(p₀ = 0); при l = 1_p1 =

h

2π

  √2.

При описании вращения частицы по сфере, помимо момента вращения, важно охарактеризовать проекцию этого момента на ось z. Эта проекция определяется значением величины т:

p_z = mh/2π.

По причинам, которые будут ясны далее, т носит название магнитного квантового числа. Анализ уравнения (XXI.20) показывает, что т ≤ l. Таким образом, для данного значения l величина т изменяется от -l до +l, т.е. принимает 2l + 1 значений.

Рассмотрим функции η для наименьших значений квантовых чисел. При l = 0 т может также равняться лишь нулю ψ_{i = 0, m = 0}, = B, где В - постоянная величина.

В основном состоянии ротатора, следовательно, волновая функция не дает никакой информации о положении частицы. С этим связано отсутствие нулевой энергии у ротатора. Действительно, при l = 0, согласно уравнению (ХХII.19) E = 0.

Мы видели на примерах потенциального ящика и осциллятора, что чем точнее определено положение частицы, тем больше величина нулевой энергии.

При l = 1 т может иметь значения -1; 0 и +1 и соответственно

ψi = 1;	m = 0 ∼ cosθ;
ψi = 1;	m = +1 ∼ sinθeiφ;
ψi = 1;	m = -1 ∼ sinθe-iφ

Из величины проекции момента p_z и значения самого момента р может быть рассчитано значение угла а между осью z и моментом: соs α = p_z/p = m/√l(l + 1).

Дискретность допустимых значений m означает, что разрешены только некоторые направления момента (пространственное квантование).

565