Волновое уравнение описывает ряд специфических особенностей микрообъектов. Мы рассмотрим их на примере решения отдельных, важных для дальнейшего изложения задач. В качестве первой такой задачи мы рассмотрим простейшую модель металла, о которой уже была речь в гл. XIII,- модель потенциального ящика.
В этой модели задача многих электронов приближенно сводится к задаче одного электрона. Каждый электрон движется в поле остальных электронов и ядер. Это поле представляется в виде некоторой постоянной потенциальной энергии внутри металла. Мы рассмотрим простейший случай, приняв эту энергию бесконечно большой, и, следовательно, будем пренебрегать вероятностью выхода электрона из ящика.
Уравнение Шредингера для линейного случая:
+
(
E -
U)ψ = 0.
или
+
Eкψ = 0,
553
+ Bψ = 0,
(XXII.1)
где
B =
Eк.
Если металл занимает длину l, то краевые условия запишутся как ψ(0) = 0 и ψ(l) = 0. Эти условия вытекают из того, что из-за бесконечно большой глубины ящика электрон не должен проникать за его пределы.
Общее решение уравнения (XXII.1):
ψ = A(sin√Bx + α),
где В и α - постоянные.
Из условия ψ(0) = 0 следует, что α = 0.
Из условия ψ(l) = 0 следует, что √Bl = nπ, где n = 1, 2, 3... Следовательно:
Eк =
n2.
(XXII.2)
Энергия частицы, движущейся в потенциальном ящике, следовательно, может иметь определенные дискретные значения. В этом проявляется одно из важнейших новых качеств микрочастиц - квантование энергии. Мы уже сталкивались с этим при рассмотрении энергии колебания (гл. XII). Физический смысл квантования делается более ясным, если выразить Ек через импульс и определить набор разрешенных значений скоростей.
Подставляя вместо Eк = p2/2m и решая уравнение относительно р, получим
p = (h/2l)n.
Это уравнение может быть переписано следующим образом: так как p = h/λ, то
= n.
(ХХII.3)
Квантование волн имеет тот же смысл, что и существование дискретного набора частот струны. На длине l должно укладываться целое число полуволн. Квантование волн приводит к квантованию импульса, а последнее - к квантованию энергии.
Из уравнений (XXII.2) и (ХХII.3) вытекает еще одно
554
важнейшее свойство микрочастиц, описываемое волновой механикой. Набор значений п начинается с единицы. Если n = 0, то это означает лишь, что частицы в ящике нет. Действительно, в этом случае функция ψ не может быть нормирована, т.е. удовлетворять условию ∫φ2dx = l.
При всех значениях п, не равных нулю, коэффициент А может быть подобран таким образом, чтобы удовлетворить этому условию.
При n = 0 волновая функция ψ просто равна нулю, и это означает отсутствие частицы. Так как п начинается с единицы, то имеется наибольшее значение длины волны и, следовательно, наименьшее значение энергии, которой может обладать частица в потенциальном ящике. Эта наименьшая энергия носит название нулевой. Согласно уравнению (XXII.2): Eнул = h2
Мы видим, что нулевая энергия зависит от размера ящика и возрастает с уменьшением этого размера. Микрочастица не может находиться в малом объеме, не имея большой -кинетической энергии. В частности, отсюда следует вывод о том, что электрон отсутствует в ядре. Размер "ящика" в этом случае очень мал, и поэтому энергия электронов должна быть очень велика. Расчет, сделанный с учетом теории относительности, показывает, что нулевая энергия электрона в ядре должна быть в несколько раз больше энергии его связи.
Следовательно, нулевой энергии.достаточно для удаления электрона из ядра, поэтому электроны не могут находиться в ядре.
Каковы физические причины, приводящие к наличию нулевой энергии? По Гайзенбергу, для того чтобы фиксировать частицу в малом объеме, ее нужно осветить светом с очень малой длиной волны. Однако малой длине волны отвечает по уравнению (XXI.4) большое значение импульса и энергии кванта, которая будет передана наблюдаемой частице.
Уравнение (ХХII.3) представляет основу для правильного толкования нулевой энергии. Нулевая энергия отвечает основному тону струны и является следствием волновых свойств, реально существующих у микрочастиц.
Для рассмотрения движения частицы в трехмерной прямоугольной яме следует решить следующее уравнение:
+
+
+
Eкψ = 0.
(XXII.4)
Искомая функция ψ может быть представлена как произведение
555
трех функций, каждая из которых зависит только от одной координаты:
ψ(x; y; z) = X(x)Y(y)Z(z)
(ХХII.5)
Если подставить это уравнение в (XXII.4) и разделить на X, Y, Z, то получим:
+
+
+
(
Ex +
Ey +
Ez) = 0;
Это уравнение распадается на три:
+
ExX = 0;
+
EyY = 0;
+
EzZ = 0
Решение этих уравнений соответствует полученному выше для одномерного случая. Соответственно

где a, b и с - длины сторон ящика.
Уравнение (XXII.5) отвечает известному соотношению, согласно которому вероятность сложного события равна произведению вероятностей соответствующих простых. Множители в этом уравнении описывают соответствующие плоские волны.
В качестве второй задачи на применение уравнения Шредингера мы весьма приближенно рассмотрим вопрос об осцилляторе, т.е. упруго связанной с некоторым центром частицы. В этом случае потенциальная энергия частицы зависит от координат.
Для гармонического осциллятора (см. гл. XII) U = kx2/2.
Уравнение Шредингера для линейного осциллятора запишется следующим образом:
+
(
E -
)ψ = 0.
Аналогом этой задачи является определение стоячих волн на неоднородной струне. Необходимо определить ψ и разрешенные значения Е, при которых выполняются краевые условия: ψ(±∞) = 0.
Мы не будем рассматривать полного решения возникающей математической задачи. Нетрудно определить вид искомых функций на большом расстоянии от начала координат.
556
Действительно, для больших х уравнение (XXII.4) перейдет в следующее:
(d2ψ/dx2) - B2x2ψ = 0,
где B2 = 4π2mk/h2.
Решение этого уравнения в рассматриваемой области запишется следующим образом:
ψ = e-Bx2/2.
Можно искать решения исходного уравнения в виде Ae-Bx2/2П(x),
где П(х) должен быть многочленом для того, чтобы не изменять свойства функций при х = ∞.
Можно показать, что это требование удовлетворяется, если E = hν(n + l/2), где п - целое положительное числе, изменяющееся от нуля до бесконечности. Каждому значению п отвечает определенная собственная функция.
Выпишем и обсудим собственные функции, отвечающие первым двум квантовым числам:
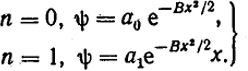 (ХХII.7)
При n = 0 E = nν2.
(ХХII.8)
(ХХII.7)
При n = 0 E = nν2.
(ХХII.8)
Эта наименьшая возможная энергия осциллятора является нулевой. Упругосвязанная частица, обладая такой энергией, не покоится в точке x = 0. Вероятность найти ее на расстоянии х описывается уравнением (XXII.5). Чем больше k, тем больше В, следовательно, тем меньше вероятность найти частицу на большом расстоянии от точки равновесия, тем в меньшем объеме "находится" частица.
Вместе с тем нулевая энергия, согласно уравнению (XXII.6), растет с величиной ν и, следовательно, k.
Таким образом, снова, как и в задаче с потенциальным ящиком, нулевая энергия тем больше, чем в меньшем объеме оказывается частица. В основном состоянии (n = 0) Наиболее вероятно, согласно уравнению (XXII.5), частицу найти в точке х = 0. Классическим аналогом этого состояния является состояние покоя. Квадрат собственной функции для состояния, отвечающего n = 1 с энергией E = 3hν/2, имеет максимумы на некотором расстоянии от центра. Классическим аналогом этого состояния является
557
колебание частицы, характеризуемой определенной амплитудой.
Наличие нулевой энергии имеет существенное значение для понимания ряда явлений и особенно изотопного равновесия.
Как показывает практика, изотопы не распределяются равномерно между разными молекулами. Например, равновесие реакции D + H - H = H + D - H сдвинуто в сторону замещения водорода в молекуле водорода на дейтерий. Почему же свободная энергия системы снижается при замене водорода в молекуле на дейтерий? Более детальное рассмотрение показывает, что существенную роль в изотопных равновесиях играют тепловые эффекты.
Оказывается, например, что энергия диссоциации молекулы D2 (439 кДж/моль) существенно больше энергии диссоциации Н2 (431,95кДж/моль). Почему же труднее разорвать D2 по сравнению с Н2? Ведь энергия химического взаимодействия определяется взаимодействием электронов, а движение их практически одинаково в молекуле D2 и Н2. Поэтому кривые, определяющие энергию притяжения атомов (потенциальные кривые), одинаковы для обеих молекул. Эта кривая, общая для обеих молекул, изображена на рис. XXII.1 (нижняя пунктирная кривая). Смысл других кривых будет объяснен в гл. XXIII § 3. На оси абсцисс отложено расстояние между атомами, а на оси ординат - энергия их взаимодействия. По мере приближения атомов энергия понижается и, пройдя при равновесном
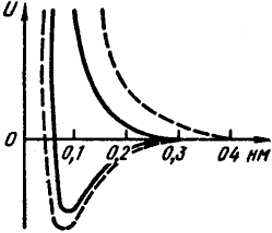
Рис. XXII.1. Потенциальная энергия молекулы водорода (пунктирные линии передают опытные значения)
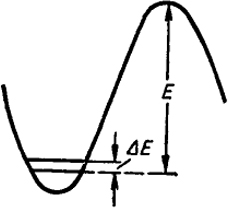
Рис. XXII.2. Схема, объясняющая зависимость энергии активации от изотопного состава
558
расстоянии через минимум, начинает при дальнейшем сближении атомов повышаться. Величины равновесного расстояния и величины минимума энергии для Н2 и D2 одинаковы, и все же энергии диссоциации различны. Дело в том, что молекулы имеют нулевую энергию, и энергия диссоциации должна отсчитываться от уровня этой нулевой энергии до принятой за нуль энергии разделенных атомов. Между тем, так как, согласно уравнению (XXII.6), нулевая энергия определяется через частоту, а частота зависит от массы, то уровни нулевой энергии должны быть различны. Таким образом, различие в энергиях диссоциаций молекул дейтерия и водорода должно определяться различием их нулевых энергии (см. гл. XIII).
Известно, что ν = (1/2π)√k/μ.
Постоянная k должна быть одинаковой для Н2 и D2 величина μ определяется соотношением 1/μ = l/m1 + 1/m2.
В случае одинаковых атомов μ = m/2. Для D2, следовательно, μ вдвое больше, чем для Н2 и соответственно νD2 = νH2/√2. Другими словами, нулевая энергия молекул дейтерия на 40 % меньше нулевой энергии молекулы водорода. Эта разница нулевых энергий Н2 и D2 близка к двум большим калориям.
Разница в теплотах, естественно, скажется на изотопном равновесии, как это следует из уравнений гл. XIII. Различие в нулевых энергиях еще значительнее сказывается на скоростях процессов.
Как указывалось в гл. XVI, скорость химических реакций существенно определяется энергией активации Е.
Как видно из рис. XXII.2, энергия активации должна также отсчитываться от уровня, отвечающего нулевой энергии. Из этого рисунка также видно, что энергия активации будет больше для реакций с участием тяжелого изотопа. Разница энергий активации ΔE должна равняться разнице нулевых энергий. При комнатной температуре различие энергии активации на 7 кДж/моль изменит скорость реакции в 10 раз.
Одной из совершенно новых особенностей микрочастиц, описываемых уравнением Шредингера, является способность проникать через барьер, или так называемый "туннель-эффект". Если классическая, частица встречает на своем пути потенциальный барьер и ее энергия меньше энергии вершины барьера, то она упруго отразится и не сможет проникнуть" за барьер. Между тем микрочастица имеет конечную вероятность совершить этот процесс.
559
Задача проникновения через потенциальный барьер очень часто встречается в физике. Рассмотрим, например, процесс α-распада, при котором α-частица покидает ядро радиоактивного элемента. Каково взаимодействие α-частицы и ядра? На больших расстояниях между ними должно иметь место кулоновское отталкивание, поскольку и ядро, и α-частица имеют положительный заряд. Однако на близких расстояниях (∼10-13 см) включаются специфические ядерные силы, обеспечивающие прочность ядер, и энергия α-частицы должна понижаться. В итоге возникает зависимость потенциальной энергии вазимодействия α-частицы с ядром, изображенная на рис. ХХII.З.
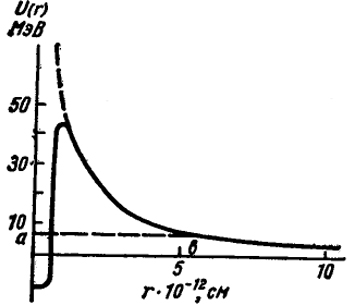
Рис. ХХII.З. Энергия взаимодействия α-частицы и ядра
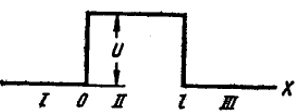
Рис. XXI 1.4. Схема потенциального барьера
Уровень ab изображает энергию α-частицы в ядре. Из рисунка видно, что для того, чтобы покинуть ядро, α-частица должна просочиться через барьер.
При любой химической реакции электроны проходят сквозь потенциальный барьер. Действительно, электронам необходимо покинуть атомные орбиты и перейти на молекулярные. Этот переход; связанный с необходимостью пройти через область повышенной энергии (отрыв от атома), осуществляется как туннель-эффект.
В гл. XVIII мы рассмотрели процесс разряда иона водорода при электролизе. При этом, как и при химической реакции, электрон также просачивается через барьер, хотя
560
скорость всего процесса и не лимитируется этой стадией.
Выход электронов из металла под влиянием электрического поля связан с прохождением сквозь потенциальный барьер.
Молекула аммиака представляет собой пирамиду, в вершине которой находится азот. Молекула может "вывернуться", т.е. перейти из состояния, в котором азот находится по одну сторону плоскости атомов водорода, в состояние, при котором он будет находиться по другую сторону путем туннель-эффекта. При этом в системе произойдет переход через потенциальный барьер, вершине которого отвечает плоская молекула.
Рассмотрение барьера с толщиной /, состоящего из плоских отрезков, упрощается, поскольку решение уравнения Шредингера для постоянной потенциальной энергии (рис. XXII.4) не представляет трудности и было уже рассмотрено нами выше.
Для всех трех областей, изображенных на рис. XXII.4, уравнение Шредингера запишется следующим образом:
(d2ψ/dx2) + Bψ = 0,
(XXII.9)
где постоянная В = (8π2m/h2)(Е - U).
Общее решение уравнения (XXII.7) запишется как
ψ = Ae±√-Bx.
(XXII.10)
В первой и третьей областях В > 0 и решение (XXII.8) описывает водный. Во второй области В < 0 и ψ-функция передается экспоненциальной, а не периодической:
ψ = A1e-√-Bx + A1e + √-Bx.
Если толщина барьера бесконечно велика, то частица не сможет проникнуть сквозь него. Поэтому при x → 0 ψ = 0. Следовательно, A2 = 0.
Таким образом, внутри потенциального барьера функции экспоненциально убывают по закону:
ψ∥ = A1e√-Bx.
(XXII.11)
Во второй области потенциальная энергия больше общей энергии частицы. Это означает, что кинетическая энергия отрицательна. Отрицательной кинетической энергии отвечает мнимая скорость. Это означает, что понятие скорости, как и вообще понятие частицы, в этой области лишено смысла. Аналогичный эффект имеет место и в задаче с осциллятором. Действительно, в соответствии
561
с уравнением (XXII.5), для собственной функции колеблющейся частицы имеется конечная вероятность обнаружить ее на сколь угодно больших расстояниях, в том числе и на расстояниях, на которых ее потенциальная энергия больше кинетической.
Волновым аналогом экспоненциального убывания вероятности найти частицы за барьером конечной толщины может быть проникновение через тонкие пластины падающего луча при условии полного внутреннего отражения. Световое поле проникает на некоторую глубину, и поэтому тонкая пластинка пропустит некоторое количество света и в условиях полного внутреннего отражения. Таким образом, в проникновении через барьер проявляются волновые свойства частиц.
Вероятность (ω) проникновения через барьер должна быть пропорциональна отношению вероятностей найти частицу по обе стороны барьера. В соответствии с этим

или, учитывая формулу (XXII.9);
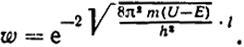 (XXII.12)
(XXII.12)
Мы видим, что вероятность проникновения резко убывает с увеличением массы частицы, толщины барьера и величины недостачи энергии частицы до необходимой для достижения вершины барьера. Отметим, что, как и все квантовые эффекты, вероятность проникновения исчезнет, если принять h → 0.
Уравнение (XXII.10) объясняет, почему барьеры часто не являются препятствием для электронов, в то время как для тяжелых частиц туннель-эффект наблюдается весьма редко. Наличие этого эффекта для а-распада объясняется малостью толщины барьера l.
Было высказано предположение, что мартенситное превращение, для которого требуются также весьма малые перемещения атомов, протекает по механизму туннель-эффекта. Доводом в пользу такого предположения является протекание этого процесса при весьма низких температурах. Теория α-распада, как туннель-эффекта, позволила объяснить одну из наиболее важных особенностей этого процесса.
562
Вид потенциальной кривой, изображенной на рис. XXII.4, мало меняется при переходе от одного тяжелого ядра к другому (α-радиоактивность наблюдается лишь у тяжелых ядер). Чем выше энергия α-частицы, тем больше вероятность вылета ее из ядра и тем меньше будет время полураспада соответствующего радиоактивного элемента.
В качестве следующего примера применения уравнения Шредингера мы также приближенно рассмотрим вращение частицы, т.е. задачу ротатора.
563
