Часть четвертая
СТРОЕНИЕ ВЕЩЕСТВА
Во введении к книге указывалось, что с учением о строении атомов и молекул связана третья группа методов физической химии.
Термодинамика классифицировала большой экспериментальный материал на основе трех опытных принципов.
Статистическая механика вскрыла механизм процессов и позволила свести термические (теплота, теплоемкость и др.), термодинамические (энтропия, свободная энергия и др.) и кинетические (коэффициенты диффузии, вязкости и др.) характеристики к микроскопическим (радиусы молекул, частоты колебаний, энергии связей и др.). Однако эти микроскопические характеристики не являются первичными и могут быть сведены к характеристикам элементарных частиц, из которых состоят атомы и молекулы. При решении подобных задач обычно осуществляются следующие стадии.
Сначала выясняется, из каких частей состоят исследуемые объекты, затем как расположены эти части и, наконец, по каким законам они движутся.
С восьмидесятых годов прошлого столетия в физике начался период так называемых электронных явлений.
В 1881 г. Г. Гельмгольц впервые высказал предположение о существовании "атомов" электричества - электронов. Г. Гельмгольц рассмотрел молекулярный смысл числа Фарадея. Если разделить соответствующий этому числу заряд грамм-эквивалента на число Авогадро, то должен получиться наименьший заряд одного иона. Так, Г. Гельмгольц впервые оценил заряд электрона. В течение нескольких Десятков лет физики изучали свойства элементарных зарядов.
По отклонению потока заряженных частиц в разрядных трубках в электрическом и магнитном полях удавалось оцепить отношение заряда к массе электронов. Было показано, что носители тока в металлах являются электронами
540
и имеют то же отношение заряда к массе (эффект Толмена - возникновение электродвижущей силы в заторможенной катушке и эффект Холла - возникновение электродвижущей силы при действии магнитного поля на электрический ток в металле, см. гл. XXIII).
Было показано, что заряженные частицы, вылетающие из металла, при воздействии света (фотоэффект) или при нагревании (термоэффект), также являются электронами.
Р. Милликен определял заряд весьма малых капель, изучая равновесие их в электрическом поле конденсатора. Оказалось, что заряд их равен или превышает величину, являющуюся наименьшим зарядом (е = 1,602·10-19 Кл) и кратен ей. Измерение отношения заряда к массе ионов в разрядных трубках показало, что носители положительного заряда всегда имеют массу, значительно превышающую массу электрона. Оказалось, что наименьшей массой среди положительных ионов обладает протон. Среди носителей отрицательного заряда выделяется электрон, масса которого в 1839 раз меньше массы протона.
Для выяснения важного вопроса о том, как расположены составные части атома, Э. Резерфорд изучал рассеяние веществом потока α-частиц (положительно заряженные частицы) - одного из радиоактивных излучений. Характер отклонения α-частиц от своего пути при прохождении через вещество показывал наличие сосредоточенных положительных зарядов в его объеме. Так возникла нуклеарная модель атома, согласно которой электроны вращаются вокруг малого ядра, где сосредоточен положительный заряд. Опыты Э. Резерфорда позволили оценить заряд и радиус ядер. После этих опытов физика атома разделилась на физику ядра и физику электронов.
Уже первое рассмотрение нуклеарной модели показало, что электроны не подчиняются законам классической механики. Действительно, периодическое движение (вращение) заряженной частицы должно приводить к излучению. Следовательно, электрон должен, быстро теряя энергию, "упасть" на ядро, испустив при этом излучение, характеризующееся непрерывным спектром, так как частота вращения падающего электрона непрерывно увеличивается. Однако атомы стабильны, а спектры их дискретны.
Мы уже сталкивались при рассмотрении третьего принципа термодинамики (см. гл. IV), и особенно статистической механики (см. гл. XII), с некоторыми положениями квантовой механики и, в частности, с наличием дискретного набора уровней энергии.
541
Дискретность энергий и вообще состояний проявляется не только в спектрах, но и во многих свойствах электронов и всех микрочастиц. Остановимся на двух классических опытах.
В опыте И. Франка и Г. Герца исследовались потери энергии медленных электронов, проходящих через пары ртути (при давлении ∼1 мм рт. ст.). Первоначальная энергия электронов могла непрерывно изменяться в зависимости от потенциала, в котором электроны разгонялись.
Измерялся ток, идущий от собирающей пластинки к земле. При этом тормозящее поле задерживало электроны, потерявшие скорость в результате столкновений с атомами ртути. Оказалось, что при малой энергии (меньше 4,9 эВ) электроны, вопреки законам классической механики, проходят через пар ртути, практически не теряя энергию. Как только энергия электронов достигает указанной величины (4,9 эВ), электронный ток падает, так как проходящие электроны теряют энергию, возбуждая переход электронов атомов ртути на первый разрешенный уровень. При дальнейшем повышении энергии фиксируется ряд максимумов и минимумов в кривой зависимости тока от потенциала.
В опыте У. Штерна и В. Герлаха пучок атомов проходил в неоднородном магнитном поле. В однородном поле имеет место ориентация магнитных моментов атомов, в неоднородном должно происходить движение атомов в направлении градиента поля. Это направление перпендикулярно направлению движения атомов, поэтому магнитное поле должно вызывать отклонение пучка.
Сила, действующая на атом, должна зависеть от величины магнитного момента атома и от ориентации этих моментов по отношению к полю.
По законам классической механики возможны все ориентации момента. Однако опыт показал, что пучок атомов расщепляется на несколько пучков. Это означает, что возможны не все, а только определенные значения угла между направлением поля и магнитного момента атома.
Формулировка новой механики всегда является трудным и болезненным процессом. Огромный опыт объяснялся законами классической механики. Естественно, что при возникновении нового опыта, противоречащего известным законам механики, описывающей первичные свойства материи, возникает тенденция подправить механику какими-либо запретами, исключениями, сохранив в основном ее понятие и законы. Такой паллиативной механикой являете механика Бора-Зоммерфельда (см. гл. XII).
542
В теории Бора-Зоммерфельда не только сохраняются все понятия классической механики (координаты, скорости), но и все ее уравнения, следовательно, и орбиты. Устойчивыми, однако, признаются лишь те орбиты, при которых выполняются условия Бора - Зоммерфельда (см. гл. XII):
∮pi d qi = nih,
(XXI.1)
где qi - обобщенная координата; рi - обобщенный импульс, определяемый соотношением pi = ∂Eк/∂qi,
где
qi = dqi/dτ,
Ек - кинетическая энергия; ni - целое число; h - постоянная Планка.
Ранее (см. гл. XII) была рассмотрена энергия осциллятора по теории Бора-Зоммерфельда и было показано, что следствием уравнения (XXI.1) является дискретный спектр энергии, что привело к формулам Планка для излучения абсолютно черного тела, а Эйнштейна и Дебая - для теплоемкости. Теория Бора-Зоммерфельда позволила объяснить основные черты спектра атомов. Линейность спектров являлась следствием дискретности энергий, а квантовые числа оказались непосредственно связанными с числами ni в уравнении (XXI.1).
Однако многочисленные противоречия между теорией и опытом и невозможность охватить целые области опыта (например, молекулы) показали, что паллиативная механика Бора-Зоммерфельда не является адекватным выражением свойств микрочастиц. Требовалась ломка основных понятий, а не отбор некоторых орбит в качестве разрешенных. Такими основными понятиями, на которых базировалась физика XIX в., были понятия частицы и волны. Каждому этому понятию соответствовал определенный математический формализм. Любое сложное явление сводилось и математически описывалось на основе этих элементарных понятий. Частица - это сосредоточение вещества в некоторой части пространства, поэтому прежде всего она характеризуется координатой и импульсом. Законы движения частицы определяются уравнениями Ньютона. Волна в отличие от частицы описывает некоторый распределенный в пространстве и зависящий от времени периодический процесс. Таким периодическим процессом является, например, распространяющийся в некоторой среде звук или свет.
Уравнение, описывающее колебание, записывается cледующим
543
образом:
Δφ =
,
(XXI.2)
где
Δ =
+
+
;
х, у, z - координаты; τ - время; φ - отклонение колеблющейся величины; и - скорость распространения колебаний.
В случае упругих колебаний φ - отклонение частиц упругого тела от положения равновесия. В случае электромагнитного колебания φ описывает величины проекций векторов электрического и магнитного напряжений.
Выбор между механизмами частицы и волны физик XIX в. делал прежде всего на основе наличия или отсутствия явлений дифракции и интерференции. Эти явления свидетельствовали о периодическом характере процесса. Представим себе, например, явление дифракции света. Свет, пройдя через одну щель, дает на находящемся на ней экране систему периодически повторяющихся по определенному закону полос. Очевидно, что периодичность вызвана здесь не периодичностью прибора, а природой самого процесса распространения света.
К началу XX в. сложилось уверенное представление об областях применения понятий частицы и волны. Различные тела (электрон, молекула, планеты) описывались на основе представлений о частицах, свет и звук - на основе понятий волны.
Однако в XX в. на многочисленных примерах физики убедились, что одно и то же образование может вести себя в разных опытах и как волна, и как частица.
Казалось бы, не могло быть сомнения в волновой природе света, о которой свидетельствовали многочисленные явления дифракции. Однако фото- и комптон-эффекты противоречили этому представлению. Основная особенность фотоэффекта заключается в том, что энергия электрона, вылетающего из металла под влиянием освещения, не зависит от интенсивности света. Оказалось, что энергия этого электрона зависит лишь от частоты падающего на металл света. С классической точки зрения эти закономерности не понятны. Упруго связанный в металле электрон должен был раскачиваться полем света, и энергия, им воспринятая, должна была бы зависеть от интенсивности света.
544
Однако все явления просто и полно описываются, если Принять, что свет представляет собой поток сгустков энергии. Так как энергия осцилляторов, испускающих или поглощающих свет, кратна hν (см. гл. XII), то А. Эйнштейн, естественно, принял, что энергия этой порции излучения (кванта) равна hν.
Электрон металла, поглотив квант энергии, затратит часть ее на работу выхода (В), сохранив остаток в виде кинетической энергии.
Таким образом, hν = B + mυ2/2.
Это уравнение в точности соблюдается; оно дает, в частности, способ определения численного значения величины h.
Если фотоэффект свидетельствует об определенной дискретной энергии кванта (фотона), то комптон-эффект доказывает наличие импульса фотона. Если энергия фотона велика сравнительно с энергией связи электрона, то обычно электрон не поглощает всей энергии кванта.
Кинетическая энергия вылетающего электрона меньше энергии фотона. Остаток энергии представлен в виде рассеянного при этом процессе фотона.
Оказалось, что все количественные связи (между углами, скоростью электрона и частотами) можно получить, если, помимо закона сохранения энергии, применить закон сохранения импульса.
Энергии ε = hν фотона должен отвечать некоторый импульс р. В гл. XIII было показано, что
p = hν/c.
(XXI.3)
Комптон-эффект подтвердил наличие импульса у фотонов, описываемого формулой (XXI.3).
Таким образом, свет ведет себя в одних явлениях как периодически распределенный в пространстве процесс (волна), а в других - как частица (фотон). Это противоречие волна - частица распространяется и на частицы. Действительно, оказалось, что электроны дают дифракционные явления как на искусственных дифракционных решетках, так и на кристаллических телах.
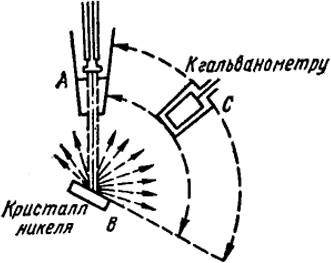
Рис. XXI.1. Схема опыта Дэвисона и Джернера
545
На рис. XXI.1 показана схема классических опытов Девисона и Джермера. Пучок электронов из электронной пушки А попадает на грань кристалла В. Фарадеев цилиндр С измеряет интенсивность отраженного пучка. Опыт показал, что зависимость этой интенсивности от угла между нормалью к грани и рассеянным лучом подчиняется уравнению Брегга, которое описывает дифракцию рентгеновских лучей - см. формулу (XXIV.1).
Позднее аналогичные дифракционные явления были обнаружены для пучков атомов и молекул, например, атомов гелия, отраженных от кристаллов LiF, нейтронов от кристаллических решеток и др.
При этом длина волны, отвечающая частице с импульсом р, находится в соответствии с формулой (XXI.3), описывающей противоречие волна - частица для света. Эта формула может быть переписана следующим образом:
λp = h.
(XXI.4)
Уравнение (XXI.4), таким образом, справедливо и для частиц, и для света и соединяет величину импульса и длину волны, которые характеризуют один объект.
Наблюдения волновых свойств частиц вызвали попытку отказа от представления о частице и толкования частицы как волнового явления, т.е. как распределенного в пространстве процесса. Такая концепция была развита Л. де Бройлем и Э. Шредингером.
Каждой частице, по Л. де Бройлю, отвечает некоторый волновой процесс, характеризующийся определенными значениями частоты и длины волны.
Эти величины определяются уже ранее рассмотренными нами уравнениями:
λ = h/p; ε = hν,
(XXI.5)
где ε - энергия частицы.
Скорость распространения колебания и определяется через ν и λ:
u = λν.
(XXI.6)
Подставив формулу (XXI.5) в (XXI.6) и учитывая в соответствии с теорией относительности, что
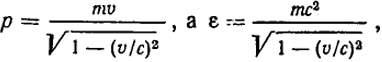
получим u = c2/υ.
Мы видим, что скорость распространения колебаний
546
(как называемая фазовая скорость) всегда больше скорости света.
Согласно теории относительности, перенос энергии или сигнала со скоростью, большей скорости света, невозможен. Что же в рассматриваемой волновой картине отвечает скорости частицы и ее координате?
Л. де Бройль ввел представление о пакете волн. Частице отвечает не одна волна, а их группа с близкими значениями длин волн. Интерферируя эти волны только в некотором малом пространстве, дают отличное от нуля значение колеблющейся величины. Очевидно, что координата этой области пространства и отвечает координате частицы.
Если скорость распространения колебания не зависит от длины волны, то скорость движений этой области, естественно, совпадает с фазовой скоростью. Однако из уравнения (XXI.6) следует, что волна электрона в отличие от волны света должна обладать дисперсией в пустоте. Действительно, наличие связи между ε и р должно привести к зависимости скорости распространения волны от ее длины. Рассмотрение вопроса показывает, что благодаря этой дисперсии скорость перемещения областей, в которых отклонения колеблющейся величины существенны, равна скорости частицы ν. Таким образом, в рамках волновой картины приобретают смысл координата и скорость частицы.
Э. Шредингер волновое уравнение (XXI.2) распространил на "волны материи".
В случае заданной энергии, согласно уравнению (XXI.5), задается значение частоты v. Состояние, при котором все точки колеблются с одинаковой частотой, но различной амплитудой, носит название стоячей волны. Основной характеристикой такого состояния является распределение амплитуды колебания в пространстве. Найдем это распределение для "волн материи". Для этого выразим величину отклонения φ через амплитуду ψ и частоту ε:
φ = ψe2πνiτ.
(XXI.7)
Подставив уравнение (XXI.7) в (XXI.2), получим:
Δψ +
ψ = 0.
Введя вместо u/ν = λ = h/p, получим:
Δψ +
ψ = 0,
где p2/2m = Eк = E - U;
547
Ек - кинетическая энергия; U - потенциальная энергия; Е - вся энергия частицы.
Тогда
Δψ +
(E - U)ψ = 0.
(XXI.8)
Уравнение (XXI.8) носит название уравнения Шредингера и является основой механики микромира. В этом уравнении задаются масса частицы т и поле U, в котором частица движется. Искомыми являются функции ψ и энергия Е. Из одного уравнения обе эти величины можно определить, потому что, помимо уравнения, задаются краевые условия.
Для электрона в атоме водорода потенциальная энергия описывается функцией U = е2/r, где r - расстояние электрона от ядра; е - заряд электрона.
Знак "минус" отвечает тому, что за нулевой уровень отсчета энергии принимается энергия электрона, удаленного на бесконечное расстояние от ядра. Очевидно, что для конечных значений r энергия должна быть ниже, т.е. меньше нуля. Краевое условие запишется следующим образом: ψ(r = ∞) = 0.
Так как энергия колебаний пропорциональна квадрату амплитуды, то Шредингер принял, что доля частицы в каждом элементе пространства определяется квадратом амплитуды г∣?. Если ψ - комплексная величина, то эта доля определяется квадратом модуля ψ–ψψ. Таким образом, в элементе объема dτ находится часть частицы, равная ψψdτ. Отсюда следует, что
∫ψψdτ = 1.
(XXI.9)
Другими словами, функция ψ должна быть нормирована, удовлетворяя соотношению (XXI.9).
Функции ψi и ψk, относящиеся к разным значениям энергии Ei и Ek, всегда ортогональны, т.е. ∫ψiψkdτ = 0. Уравнение (XXI.8) может быть записано следующим образом: Hψ = Eψ, где Н - оператор, воздействующий на функцию (ψ) и называемый оператором энергии или оператором Гамильтона.
Н = -(h2/8π2m)Δ + U.
Первый член этого уравнения передает оператор кинетической энергии, второй - оператор потенциальной энергии.
548
Общей формулировкой квантовой механики является следующее положение. Каждой физической величине отвечает определенный линейный оператор. Линейность оператора L означает, что L(c1f1 + c2f2) = c1Lf1 + c2Lf2, где f1 и f2 - функции; с1 и c2 - постоянные.
Решая уравнение Lψ = Bψ, мы находим собственные функции (fi) и собственные значения оператора (В). Оказывается, что уравнения квантовой механики могут записываться как уравнения классической механики, если заменить величины, фигурирующие в этой механике на операторы. Это положение, описывающее соответствие квантовой и классической механики, позволяет определить операторы для различных физических величин. Определение средних значений физических величин (М) производится на основе использования оператора М, отвечающего этой величине:
M = ∫ψMψdτ,
где ψ - нормированные собственные функции оператора. Энергия Е может быть выражена через функцию ψ. Для этого умножим обе части уравнения (XXI.8) на ψdτ и проинтегрируем, учитывая уравнение (XXI.9).
Тогда
E = -
∫ψΔψdτ + ∫Uψψdτ.
(XXI.10)
Второй член этого уравнения описывает потенциальную энергию электрона с учетом его распределения, передаваемого квадратом модуля собственной функции ψ. Первый член, следовательно, соответствует кинетической энергии.
Мы видим, что выражение для кинетической энергии существенно отличается от принятого в классической механике. Кинетическая энергия связана с величинами вторых производных (Δψ) и поэтому резко возрастает, когда электрон собирается в каком-нибудь малом объеме.
Можно показать, что собственная функция, удовлетворяющая уравнению (XXI.8), дает минимальную энергию Я в соответствии с выражением (XXI.10). Такая формулировка квантовой механики носит название вариационного принципа. Система выбирает собственную функцию ψ, так, чтобы энергия ее была минимальная. В частности, электрон в атоме водорода "не падает" на ядро, т.е. не выбирает "орбиты", близкой к ядру, потому что сосредоточению электрона в малом объеме соответствует резкое
549
повышение кинетической и, следовательно, общей энергии. Волновое толкование уравнения Э. Шредингера встретило ряд противоречий, и его пришлось оставить.
Прежде всего противоречива сама его запись, так как потенциальная энергия записывается как функция координат, в то время как частица "размазана" в пространстве в соответствии с квадратом модуля ψ В случае нескольких частиц4 уравнение Шредингера записывается следующим образом:
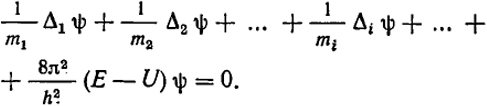 (XXI.11)
(XXI.11)
При этом
Δ1 =
+
+
; ∐
i =
+
+
,
где xi, yi, zi - координаты i-той частицы.
Функция ψ зависит от всех координат (x1, y1, z1, ..., xi, yi, zi).
Таким образом, в случае двух частиц волновое уравнение описывает колебания в шестимерном пространстве, а в случае трех частиц - в девятимерном.
Очевидно, что колебания в многомерном пространстве теряют смысл обычного колебательного процесса. М. Борн предложил другое, общепринятое в настоящее время, толкование уравнений Шредингера. Согласно этому толкованию, величина ψψdτ характеризует вероятность нахождения частицы в элементе объема dτ.
Таким образом, частица сохраняется как таковая. Сохраняется смысл радиуса частицы, ее координат, но уравнение Шредингера приобретает статистический характер, описывая лишь вероятность того или иного события.
550
