§ 2. Аксиомы термодинамики необратимых процессов

Мы рассмотрим наиболее общую формулировку аксиом термодинамики необратимых процессов, принадлежащую Онзагеру. Онзагер принял три постулата. Первый постулат позволяет описать потоки. В рассматриваемом выше примере падающих шариков их поток J (число шариков, пересекающих единицу поверхности в единицу времени) определяется уравнением J = cυ, где с - концентрация шариков; υ - скорость их движения.

Скорость шариков определяется действующей на них силой X и подвижностью U (см. гл. VIII). Таким образом J ∼ X, т.е. поток частиц пропорционален действующей на них силе. Онзагер, следуя аналогии, принял, что градиенту каждого свойства (k) отвечает некоторая сила X_k и поток каждого свойства (например, свойства i) линейно связан со всеми силами:

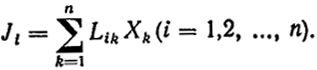(XX.1)

Силы X носят название термодинамических, а величины L_ik - коэффициенты, аналогичные подвижностям. Такая запись означает, что поток данного свойства определяется не только градиентом этого свойства, но и "чужими" градиентами (других свойств). Это взаимное влияние отвечает указанному выше возникновению одного градиента под влиянием другого.

Вторым постулатом Онзагера (также аксиоматическим)

534

является так называемое соотношение взаимности L_ik = L_ki. Оно описывает симметрию влияния термодинамичеких сил на "чужие" потоки. Если градиент свойства i (сила Х_k) действует на поток свойства k, то точно так же (на единицу силы) действует градиент свойства k на поток свойства i.

Конечно, такая формулировка была подсказана Онзагеру опытными закономерностями. Точно так же был выбран закон, определяющий термодинамические силы, без которых использование (XX.1) невозможно. Этот закон был подсказан аналогией и опытом.

Термодинамические свойства естественно связать с какой-либо термодинамической характеристикой. Мы уже обращали внимание на то, что термодинамика необратимых процессов трактует скорость изменения энтропии. Представляется интересным найти связь термодинамических сил с этой величиной. Найдем эту связь для ранее рассмотренного простейшего случая падающих шариков. Энтропия системы в этом случае растет из-за выделения тепла при трении. В единицу времени сила X, действуя на один шарик, совершит работу Хυ. В единице объема имеется с шариков, и поэтому количество выделившегося тепла составит zυc. Рост энтропии в единице объема за единицу времени (S) определится приведенным теплом. Таким образом, TS = Xυc. Так как поток шариков J = υc, то TS = XJ.

Распространяя это уравнение на любые термодинамические силы и учитывая, что общий рост энтропии определяется суммой роста, обусловленного отдельными силами, получим третий постулат Онзагера:

TS = ∑J_iX_i. (XX.2)

Это уравнение позволяет определять термодинамические силы для любого свойства. Определим тепловую силу, возникающую при наличии градиента температуры. Пусть между двумя пластинками с площадью Е, находящимися на расстоянии Δx, имеется разница температур ΔT. Определим величину S. Если порция тепла δq переходит за время Δτ от более горячей пластинки к менее горячей, энтропия возрастет на величину ΔS. При этом

ΔS = -

δq

T + ΔT

  +

δq

T

  =

δq

T2

  ΔT.

Величина

S =

ΔS

FΔxΔτ

  , а J = -

δq

ΔτF

  .

535

Знак "минус" показывает, что тепло переносится в сторону меньших температур.

Таким образом, TS = -J

1

T

 

ΔT

Δx

  .

Отсюда, согласно уравнению (ХХ.2):

X_теп = -

1

T

  gradT.

Можно показать, что химическая сила, вызванная градиентом химического потенциала ц, описывается уравнением X_хим = -Tgrad (μ/T), а электрическая, вызванная градиентом потенциала φ, Х_электр = -gradφ.

536