Расчеты изменения энтропии проводятся при помощи уравнения dS = δQ/T. При этом для получения правильных результатов необходимо, чтобы процесс, при помощи которого по калориметрическим данным определяется ΔS, был обратимым. Приведем некоторые примеры расчетов.
Чему равно приращение энтропии моля железа при температуре его плавления 1536° C (1809 К) при переходе из кристаллического в жидкое состояние, если энтальпия плавления ΔHпл = 13765 Дж/моль.
Так как при 1536° C расплавленное железо находится в равновесии с кристаллами и температура остается постоянной, то
ΔSпл = SFeж - SFeт = ΔHпл/Tпл = 13765/1809 Дж/(моль·К).
Интересно указать на существование эмпирического
44
правила Ричардса, согласно которому энтропии плавления простых веществ, в том числе металлов, близки между собой и колеблются около величины R [8,314 Дж/(моль·К)]. Так, для Cu ΔSпл = 9,57 Дж/(моль·К), а для Pb ΔSпл = 8,02 Дж/(моль·К). Для соединений обычно ΔSпл. Так, при плавлении льда (273 К) ΔHпл = 6025 Дж/моль и ΔSпл = 6025/273 = 22,07 Дж/(моль·К). Так как число способов осуществления газового или парообразного состояний намного превосходит соответствующее число для конденсированных состояний (твердого и жидкого), то изменение энтропии при испарении значительно больше, чем при плавлении. Например, при испарении моля воды при 100° C ΔHисп = 40590 Дж/моль и, следовательно,
ΔSисп = SH2Oг - SH2Oж = ΔHисп = 40590/373 = 108,83 Дж/(моль·К).
Если процесс не является изотермическим, то следует учитывать изменение энтропии при обратимом изменении температуры. Это может быть сделано при помощи уравнения dS = δQ/T = (CpdT)/T.
Например, изменение энтропии при нагревании моля воды от 0 до 100° C составит (СрH2Oж = 75,44 Дж/моль)
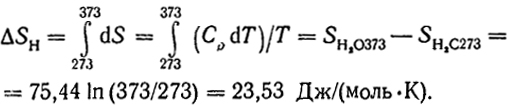
Здесь приближенно принимается, что теплоемкость воды в указанном интервале не зависит от температуры.
Приведенные результаты позволяют вычислить изменение энтропии ΔSпр при превращении моля льда при 0° C в пар при 100° C. Так как энтропия есть функция состояния, то ΔSпр = ΔSпл + ΔSисп + ΔSн = 22,07 + 108,83 + 23,53 = 154,43 Дж/(моль·К).
То обстоятельство, что изменение энтропии не зависит от пути процесса, позволяет найти разность этой функции в двух состояниях - устойчивом и неустойчивом (метастабильном), не находящихся в равновесии.
Вычислим, например, разность между энтропией переохлажденной до - 10° C (263 К) воды и энтропией льда при этой же температуре. Как следует из приведенного выше примера, энтропия жидкой воды должна быть выше энтропии льда и процесс перехода вода - лед должен сопровождаться уменьшением энтропии. Однако в этом случае
45
ΔS263 ≠ - 6025/263, так как процесс перехода из неустойчивого состояния в устойчивое происходит необратимо.
Для того чтобы найти истинное значение ΔS263, следует рассмотреть воображаемый обратимый переход переохлажденной воды в лед, например, следующим путем. Переохлажденная вода нагревается от -10 до 0° C, превращается при температуре плавления в лед, который охлаждается до -10° C:

В связи с этим следует заметить, что энтропия должна возрастать при необратимых процессах лишь в изолированных системах. Если же тело находится в тепловом контакте с другим, то его энтропия может уменьшаться за счет ее увеличения в другом теле. Так, если тело с температурой T1 отдает менее нагретому телу с температурой Т2 тепло δQ, то энтропия первого тела уменьшается на величину δQ/T2, а энтропия второго увеличится на δQ/T2 Однако общее изменение энтропии системы, состоящей из двух тел, будет положительным, т.е. -δQ/T2 + δQ/T1 < , так как T2.> T1
Найдем важное для дальнейшего изложения выражение для энтропии идеального газа как функции состояния, т.е. ее зависимость от р, V и Т. Из уравнений (1.8) и (11.14) получим основное уравнение для вычисления энтропии:
dS = (dU + pdV)/T.
(II.15)
Так как для одного моля идеального газа pV = RT и
dU = CVdT, то
dS = CV (dT/T) + R(dV/V).
(II.16)
При нагревании газа при постоянном объеме
dS = S2 - S1 = CV ln(T2/T1),
(II.17)
т.е. энтропия в этих условиях всегда увеличивается при возрастании температуры.
При изотермическом расширении ΔS = S2 - S1 =
46
= Rln(V2/V1) или с учетом того, что pV = const,
ΔS = Rln(p1/p2).
(II.18)
Энтропия идеального газа при постоянной температуре растет при увеличении объема и уменьшается при увеличении давления.
В общем случае из уравнения (II.16) следует, что
S = CVlnT + RlnV + C,
(II.19)
где С - постоянная интегрирования.
При рассмотрении изменений энтропии постоянная С исключается.
Как видно из приведенных выше соотношений, для того, чтобы вычислить изменение энтропии при процессах с реальным газом, необходимо знать уравнение состояния.
47
