Методы оценки относительной реакционной
способности мономеров
Обычный способ оценки r1 и r2 для данной пары мономеров заключается в определении состава сополимеров, образованных из нескольких мономерных смесей различного состава. Во избежание необходимости использовать интегральную форму уравнения сополимеризации при последующей оценке данных желательно, чтобы степень превращения (конверсия) не превышала 10%.
При известных составах исходной смеси мономеров и образующегося сополимера для определения r1 и r2 удобно пользоваться графическим методом Майо - Льюиса.
Для начальных стадий превращения можно принять концентрации мономеров [А] и [В] величинами постоянными и считать d[A] и d[B] концентрациями мономерных звеньев в сополимере.
241
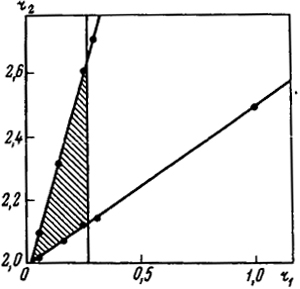
Рис. 5.5. Графическое определение относительной реакционной способности мономеров r1 и r2 по Майо-Льюису
Преобразуя уравнение (5.23), получаем следующее выражение:
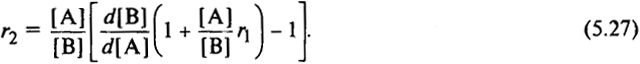
Очевидно, что в соответствии с уравнением (5.27) величина r2 линейно зависит от r1. Значения [А], [В], d[A] и d[B] являются некоторыми параметрами. Каждая пара этих параметров дает прямую линию в системе координат r1 и r2, т.е. на основании одного опыта можно построить прямую линию, а по точке пересечения линий, полученных в результате двух опытов, определить значения r1 и r2 для изучаемой системы (рис. 5.5). Но, как правило, получают три или более линий, которые из-за ошибок эксперимента не пересекаются в одной точке, а ограничивают некоторую область наиболее вероятных значений r1 и r2.
Задача. Определить константы сополимеризации акрилонитрила с 2-метил-5-винилпиридином, если при степени превращения 5% мольные доли акрилонитрила в мономерной смеси и в сополимере были следующие (1 - 5 - номера опытов):
| |
1 |
2 |
3 |
4 |
5 |
| В исходной смеси |
0,2 |
0,4 |
0,5 |
0,75 |
0,9 |
| В сополимере |
0,1 |
0,2 |
0,25 |
0,46 |
0,7 |
Решение. По формуле (5.27) рассчитываем r1 и r2.
Из опыта 1:
- а) r1 = 1; r2 = (0,2/0,8){(0,9/0,1)[1 + (0,2/0,8)1] - 1} = 2,56;
- б) r1 = 0,1; r2 = 2,056.
Из опыта 3:
- a)
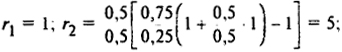
242
- б) r1 = 0,1; r2 = 1(3 · 1,1 - 1) = 2,3;
- в) r1 = 0,2; r2 = 1(3 · 1,2 - 1) = 2,6.
Из опыта 5:
- а) r1 = 0,1; r2 = (0,9/0,1){(0,3/0,7)[1 + (0,9/0,1)0,1] - 1} = - 9,8;
- б) r1 = 0,2; r2 = 9[(0,3/0,7)(1 + 9 · 0,2) - 1] = 1,8;
- в) r1 = 0,25; r2 = 9[(0,3/0,7)(1 + 9 · 0,25) - 1] = 3,5.
На основании этих расчетов строим график зависимостей r2 = f(r1) (см. рис. 5.5). Область, ограниченная тремя пересекающимися прямыми, является областью наиболее вероятных значений r1 и r2. Координаты точки пересечения трех медиан заштрихованного треугольника являются искомыми значениями r1 и r2:
r1 = 0,12; r2 = 2,35.
Для вычисления значений r1 и r2 различных пар сомономеров применяется также метод Фейнмана - Росса. Сущность этого метода заключается в следующем.
Обозначим в уравнении (5.23)
d[A]/d[B] = f; [A]/[B] = F.
Тогда

Очевидно, что это уравнение прямой у = φ(х), где у = F(f - 1)/f, а х = F2/f. По данным эксперимента строим график зависимости у = φ(х). Каждый опыт дает точку на этом графике, а серия опытов - прямую. Угловой коэффициент прямой соответствует значению r1, а отрезок, отсекаемый на оси ординат, - значению r2 с обратным знаком.
Для решения задачи рассчитываем значения F и f, а также у и х:
| F |
0,25 |
0,66 |
1,0 |
3,0 |
9,0 |
| f |
0,11 |
0,25 |
0,33 |
0,85 |
2,33 |
| у |
2,022 |
1,98 |
2,03 |
0,53 |
5,13 |
| х |
0,568 |
1,742 |
3,030 |
10,588 |
34,764 |
Строим график у = φ(х) и определяем значения r1 и r2: r1 = 0,12 и r2 = 2,41 (рис. 5.6).
Можно также проводить расчет параметров прямой у = φ(х) методом наименьших квадратов: у = - 2,47 + 0,25x σ2 = 5,68 · 10-2.
Способность различных виниловых мономеров к полимеризации и сополимеризации определяется, стерическими факторами (способностью заместителей экранировать двойную связь) и степенью поляризации.
Для полуколичественной оценки "констант сополимеризации применяется метод "Q - е". Каждая константа роста сополимерной цепи выражается четырьмя параметрами, представляющими реакционные способности и полярности обеих реагирующих частиц:
K
=
qAQA exp(-
e);
K =
qAQB exp(-
eA
eB);
243
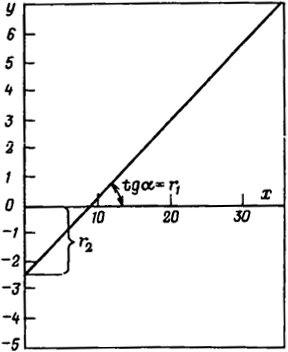
Рис. 5.6. Графическое определение относительной реакционной способности мономеров r1 и r2 по Фейнману-Россу

где q и Q - величины, пропорциональные реакционной способности макрорадикала и мономера соответственно; еA и еB - величины, характеризующие полярность мономеров А и В соответственно.
Значение е можно вычислить по следующей формуле:

где Сз - заряд; r - расстояние между зарядами в активированном комплексе; Dэ - эффективная диэлектрическая проницаемость; k - константа Больцмана; Т - температура.
При этом допускается, что заряды молекулы мономера и макрорадикала равны и постоянны, а константы сополимеризации не зависят от диэлектрической проницаемости реакционной среды.
Тем не менее, если на основании опытов по сополимеризации некоторых мономеров приписать им характеристические величины Q и е, то можно вычислить величину констант сополимеризации и для других бинарных или многокомпонентных систем, включающих эти же мономеры. Схема "Q - е" - это полуэмпирический способ определения констант сополимеризации мономеров в таких системах, где они не были определены экспериментально. Значения ri, Q и е связаны соотношениями

В Приложении 10 приведены значения Q и е для ряда мономеров, определенные на основе данных по сополимеризации. При этом в качестве основного мономера сравнения был выбран стирол и для него принято Q = 1,0 и е = - 0,8.
Задача. Для системы стирол - метилакрилат r1 = 0,75; r2 = 0,20. Рассчитать Q и е для метилакрилата. Значения Q и е для стирола принять стандартными.
Решение. Решая систему уравнений (5.31), получаем

Отсюда еA = еА ± √-ln(r1r2) = -0,8 ± l,377;
е = 0,577; е = -2,177.
244
Значения е должны быть положительными. Тогда, подставляя в одно из уравнений положительное значение еB, находим QB:
- а) 0,75 = (1/QB)ехр[0,8(- 0,8 - 0,577)]; QB = 0,44;
- б) 0,2 = QBexp[- 0,577(0,577 + 0,8)]; QВ = 0,44.
Следовательно, для метилакрилата QB = 0,44; еB = 0,577.
Задача. Пользуясь данными Приложения 10, вычислить теоретические значения r1 и r2 для процесса свободнорадикальной сополимеризации винилхлорида и акриловой кислоты.
Решение. Для акриловой кислоты: QA = 0,27; еА = 0,59. Винилхлорид характеризуется QB = 0,02; еB = 0,2.
Значения r1 и r2 определяем, пользуясь уравнениями (5.31):
- r1 = (0,27/0,02)ехр[- 0,59(0,59 - 0,2)] = 11;
- r2 = (0,02/0,27)ехр[- 0,2(0,2 - 0,59)] = 0,08.
Задача. Рассчитать QA и еА для акрилонитрила при сополимеризации его с винилхлоридом.
Решение. Из Приложений 9 и 10 находим: для винилхлорида по стиролу значения QB = 0,024 и eB = 0,2; r1 = 3,28 и r2 = 0,2.
Из уравнения (5.32)
eA = eB ± √- ln(r1r2) = 0,2 ± 1,43; e = - 1,21; e = 1,63.
Известно, что значение е для полимеров акриловой кислоты положительно. Поэтому принимаем для акрилонитрила еА = 1,63. Подставляя в первое уравнение (5.31) рассчитанные величины, получаем
3,28 = (QА/0,024)ехр[- 1,63(1,63 - 0,2)].
Отсюда QA = 0,3.
Если исследовать полимеризацию х различных мономеров с мономером, для которого известны значения Q и е, то полученные величины Q и е для остальных мономеров позволяют предсказать константу сополимеризации для х(х - 1)/2 других комбинаций мономеров.
245
