Влияние на ηэф большого числа физико-химических и энергетических факторов позволяет получать весьма важную информацию об их влиянии на гидродинамику процессов течения. Однако при этом осложняется использование гидродинамических параметров для инженерных расчетов: оценки потребляемой мощности на приготовление и транспортирование высоковязких неньютоновских жидкостей, расчета геометрии технологических трубопроводов и др.
Естественно, что для обобщения вязкостных свойств полимерных жидкостей в широком диапазоне молекулярных масс и полидисперсности, температур, концентраций, режимов течения (τ и 
) целесообразно использовать "параметры приведения", характеризующие соотношение скорости сдвига и скорости протекания релаксационных процессов: ведь ηэф представляет собой итоговую характеристику.
Каждый релаксационный процесс в реальных системах характеризуется не дискретными значениями τр, а определенным набором ("спектром") времен релаксации, в котором дискретные величины однозначно связаны между собой. Поэтому удобнее всего описывать релаксационные характеристики через "наибольшее время релаксации" τр mах. Эта величина может быть вычислена по формуле
где С - концентрация полимера в растворе; 0 ≤ а ≤ 1; 1 ≤ k ≤ 2; b = 1.
203
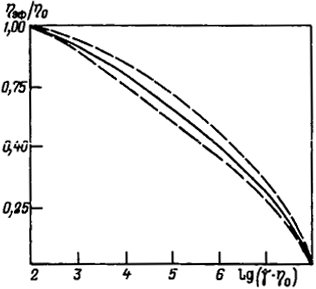
Рас. 4.22. Обобщенная характеристика вязкостных свойств концентрированных растворов и расплавов полимеров (по А. Малкину и Г. Виноградову)
В первом приближении можно принять, в соответствии с уравнением (3.18), что τp, max = f(η0). В связи этим изменение эффективной вязкости полимерных систем в процессе течения можно оценивать как ηэф/η0. Это отношение количественно характеризует отклонение реологических свойств жидкости от исходного состояния. Аналогично вычисляется "приведенный градиент скорости сдвига" - η0.
Очевидно, что η0 = (τ/ηэф)η0 = τ/(ηэф/η0). Функция ηэф/η0 = f( η0) описывается одной криволинейной зависимостью (рис. 4.22) и поэтому может быть определена как инварианта. Г. Виноградов и А. Малкин полагают возможным количественно описать эту зависимость как
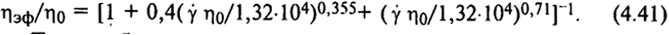
Таким образом, определяя значения ηэф при выбранных τ и , можно с достаточной надежностью определить важную физическую характеристику полимерной жидкости - η0.
Возможность использования приведенных координат ηэф/η0 - η0 позволяет при определении вязкостных свойств расплавов полимеров провести раздельную оценку влияния на них τ, Т, Mw, а также гибкости макромолекул, используя правило логарифмической аддитивности, впервые сформулированное А. Малкиным и Г. Виноградовым:
ηэф = f1(T)f2(Mw)f3(τ).
Характеристика каждой элементарной функции, входящей в это соотношение, приведена ранее.
С учетом этого имеем
lgηэф = А(Т - Тc)/[В + (Т - Тc)] + 3,4lg(Mw / Mc)
где Мc - молекулярная масса сегмента; ηс ≈ 1012 Па·с.
Однако приведенные соотношения носят в лучшем случае полуколичественный характер.
204
