В гл. 2 отмечалось, что смешение линейного или разветвленного полимера с низкомолекулярной жидкостью может привести либо к растворению, либо к образованию коллоидной системы - в зависимости от достигаемой степени дисперсности. При достижении молекулярной степени дисперсности образуются истинные растворы, для которых характерны самопроизвольность образования, равновесность, гомогенность, стабильность.
Системы полимер - растворитель, концентрация полимера в которых такова, что взаимодействием между растворенными макромолекулами можно пренебречь, называются разбавленными растворами. Концентрационной границей является величина [η]-1. Макромолекулы в разбавленном растворе представляют собой более или менее анизотропные по форме статистические клубки, способные удерживать в результате сольватации или иммобилизации некоторое количество молекул растворителя. Свободное движение таких молекулярных клубков может быть уподоблено движению сферической частицы, радиус которой соответствует большой полуоси гипотетического эллипсоида вращения, а объем ее равен объему статистического клубка. Вязкость таких растворов описывается уравнением Эйнштейна [см. уравнение (2.43)]. Однако асимметрия молекулярных клубков является причиной проявления аномалии вязкостных свойств даже в разбавленных растворах синтетических и природных полимеров вследствие ориентации таких частиц в потоке при достаточно больших т, а также из-за гидродинамического взаимодействия. При небольших и средних т разбавленные растворы полимеров являются ньтоновскими жидкостями.
Растворы полимеров, в которых отсутствует линейность концентрационной зависимости вязкости, называются концентрированными.
Вопрос. Какими структурными и термодинамическими факторами объясняется резкое увеличение вязкости концентрированных растворов с повышением концентрации полимера?
Ответ. Увеличение концентрации полимера приводит к возрастанию вязкости растворов полимеров в тем большей степени, чем: хуже термодинамическое качество растворителя; больше молекулярная масса полимера; шире молекулярно-массовое распределение (при Mw = const); жестче полимерные цепи; ниже температура раствора.
194
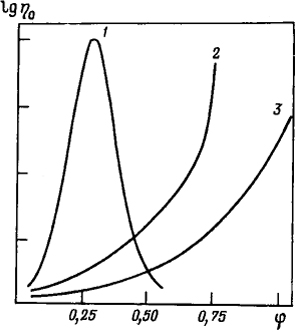
Рис. 4.17. Влияние концентрации полимеров (φ - объемная доля полимера) на эффективную вязкость концентрированных растворов полимеров:
1 - жесткоцепные полимеры (f0 < 0,63); 2 - полужесткоцепные полимеры; 3 - гибкоцепные полимеры (f0 >> 0,63)
Следует отметить неопределенность понятия "концентрированный раствор полимера", тем более что граничное условие Cк ≈ [η]-1 тоже приблизительно. Например, Дж. Ферри относит к концентрированным также растворы полимеров, в которых отношение вязкости раствора к вязкости растворителя, т.е. ηотн, больше 100. В зависимости от термодинамической гибкости макромолекул область перехода от разбавленных к концентрированным растворам составляет от долей % (мас.) - для жесткоцепных до 8-10% (мас.) - для гибкоцепных полимеров.
Условно принимают, что к среднеконцентрированным растворам можно отнести растворы, содержащие до 0,3 объемных долей полимера, с бо́льшим содержанием полимера - к высококонцентрированным. Влияние концентрации полимеров на вязкость неразрушенной структуры растворов полимеров различной гибкости иллюстрируется рис. 4.17. Возрастание η0 при увеличении концентрации происходит тем интенсивней, чем более жестки макромолекулы.
Концентрационная зависимость η0 существенно зависит от доли свободного объема системы. Согласно Фуджите - Касимото,
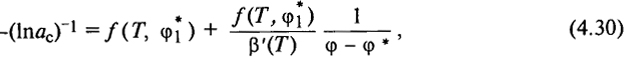
где
ac =
;
здесь η(Т, φ1) и η(Т, φ) - вязкость растворов с объемными долями растворителя φ1 = 1 - φ и φ при температуре Т, причем второй раствор (φ) выбран в качестве стандартного; f(T, φ) - доля свободного объема стандартного раствора; β’(T) - функция взаимодействия полимера с растворителем.
195
Задача. Проведите оценку постоянных величин в уравнении Фуджиты - Касимото.
Решение. Уравнение (4.30) описывается уравнением прямой в координатах (lnас)-1 - (φ1 - φ)-1, отсекающей на оси (lnaс)-1 отрезок, равный f (T, φ), и образующей с осью (φ1 - φ)-1 угол, тангенс которого равен [β’(T)]-1.
Пусть φ = 0, т.е. принимаем, что в качестве стандартного раствора выбран сам полимер. Поэтому, используя уравнение (4.30), можно оценить основные параметры уравнения состояния растворов полимера. Это уравнение справедливо для φ1 > 0,5.
Зависимость η = f (С) или η = f (φ2) описывается также уравнением Келли - Бики
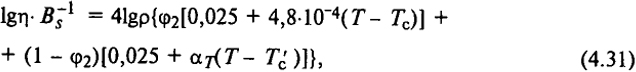
где φ2 - объемная доля полимера в растворе; Bs - параметр, включающий молекулярную массу полимера; ρ - плотность раствора; Т - температура раствора; Тс и Т - температуры стеклования полимера в твердом состоянии и в растворе соответственно; αT - температурный коэффициент свободного объема Vf.
Для полимеров обычно принимают αT = 4,8 · 10-4 град., т.е. f = 0,025 + 4,8·10-4 (T - Tc), так как f = fс = 0,025 при Тс.
Для раствора fc = 0,025 + αT(T - Тс), причем аT ≈ 10-3 град-1.
Концентрационная зависимость вязкости растворов полимеров в первом приближении может быть описана следующими соотношениями:
по Я.Френкелю -

по С. Папкову -

где А и В - постоянные для данной системы полимер - растворитель; С - концентрация полимера (по массе).
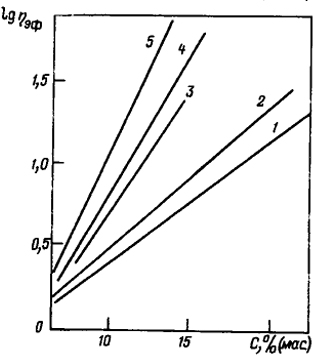
Рис. 4.18. Влияние природы растворителя на эффективную вязкость ηэф концентрированных растворов полиакрилонитрила (С - концентрация полимера) при 298 К и τ = 5 Па. Растворители:
1 - диметилформамид; 2 - диметилсульфоксид; 3 - 90%-й водный раствор этиленкарбоната; 4 - 51,5%-й водный раствор NaCNS; 5 - 60%-й водный раствор ZnCl2
196
Для ряда волокнообразующих полимеров (ХПВХ, ПАН, АЦ) может быть принято полулогарифмическое соотношение в области средних концентраций:

В этом случае значения постоянных А и В существенно зависят от термодинамического качества растворителя (рис. 4.18): его ухудшение обусловливает более резкое увеличение η0. Эти результаты свидетельствуют о том, что вязкость изоконцентрированных растворов тем ниже, чем лучше термодинамические качества растворителя. Очевидно, что уравнения (4.33) и (4.34) описывают соответствующие прямолинейные зависимости, что позволяет проводить расчетную оценку вязкостных свойств при различных концентрациях полимеров.
197
