4.5.1. Концепция свободного объема по Эйрингу - Френкелю
Любая жидкость может быть рассмотрена как система, состоящая из отдельных частиц, каждая из которых движется в некотором объеме Vf в потенциальном поле, создаваемом соседними частицами. Очевидно, что Vf соответствует объему "дырки", необходимой для движения частиц (рис. 4.13). Величина Vf называется "свободным объемом". В простейшем случае кубической упаковки шарообразных частиц жидкости каждая из них находится на расстоянии V1/3 от центра соседней частицы при условии, что положение каждой из них является равновесным. Следовательно, перемещение любой частицы по любой нормальной координатной оси возможно на расстояние, равное 2V1/3 - 2d, где d - диаметр частицы.
В связи с этим для перемещения частицы из одного равновесного состояния в другое под действием сдвигающей силы необходим свободный объем, составляющий

или в общем виде

Таким образом, свободный объем Vf при любой температуре > 0 К равен разности удельных объемов вещества при данной температуре (VT) и при 0 К (V0), т.е.
Vf = VT - V0.
Величина Vf может быть приближенно оценена из данных по скрытой теплоте парообразования жидкости, по отношению скоростей распространения звука в газе и в жидкости и другими методами.
Так, величину свободного объема Vf можно вычислить из результатов опытов по определению скорости распространения звука:

здесь С - скорость звука, м · с-1; Vm - мольный объем полимерной жидкости, м3 · моль-1; κ - показатель адиабаты, равный cp/cv, где ср и cv - теплоемкости жидкости при постоянном давлении и объеме соответственно; Mс - масса сегмента макромолекулы;
186
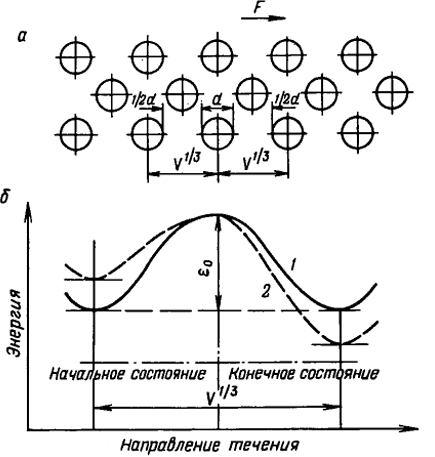
Рис. 4.13. Схема процесса течения:
а - структура идеальной жидкости (d - диаметр частицы жидкости, V1/3 - эффективное расстояние между центрами частиц, равное расстоянию между соседними положениями равновесия в процессе вязкого течения); б - барьер потенциальной энергии ε0 (1 - в покое, 2 - при течении под действием силы F)
κ = 1 + [T(αTС)2/(Jcp)],
где h - температура, К; J - механический эквивалент тепла; αT - коэффициент термического расширения жидкости.
Суммарный свободный объем соответствует объему "дырок" в жидкостях. Согласно Эйрингу,

где h - постоянная Планка; Vm - мольный объем; NA - число Авогадро; R - универсальная газовая постоянная; ΔEp - кажущаяся энергия активации вязкого течения.
Течение жидкости под влиянием приложенной силы F (эффект сдвига) может быть рассмотрено как некоторая последовательность перескоков частиц жидкости из одного положения равновесия в другое (см. рис. 4.13), для чего необходимо преодолеть потенциальный энергетический барьер высотой соответственно ε0 для одной частицы и ΔЕр - для одного моля частиц.
187
