4.3.4. Выходные эффекты (эффекты Барруса и Вайссенберга)
При значительных деформациях упругих тел простой сдвиг сопровождается возникновением нормальных напряжений (см. гл. 3). Движение растворов и расплавов полимеров в капиллярах (трубах) также приводит к проявлению нормальных напряжений как в радиальном, так и в аксиальном направлениях (эффект Вайссенберга). При выходе струи за пределы капилляра нормальные напряжения диссипируют, и наблюдается расширение струи. Это явление получило название эффекта Барруса; оно характеризуется безразмерным параметром ζ1 (рис. 4.10):

где Dc - диаметр струи в месте ее наибольшего расширения; Dт - диаметр выходного отверстия капилляра (трубы); ρT1 и ρT2 - плотности жидкости при комнатной температуре и температуре жидкости соответственно.
Эффект Барруса обусловливается:
- переходом профиля скоростей от параболического к плоскому (см. рис. 4.10);
- влиянием изменения сил поверхностного натяжения на границе жидкость - материал капилляра и жидкость - воздух и смещением равновесия струя - капля, обусловленным минимизацией поверхностной энергии;
- влиянием остаточных входовых напряжений, не успевших полностью отрелаксировать за время течения по капилляру;
- дезориентацией структурных элементов текущего полимера при прекращении действия сдвигового поля.
При пренебрежении влиянием на эффект Барруса сил поверхностного натяжения можно полагать, что

Таким образом, по степени увеличения диаметра струи жидкости, экструдируемой из капилляра, можно оценить индекс течения п.
Величина ζ0 снижается при следующих условиях:
- уменьшении ηэф полимерной жидкости;
- увеличении длины капилляра;
- уменьшении градиента скорости сдвига;
179
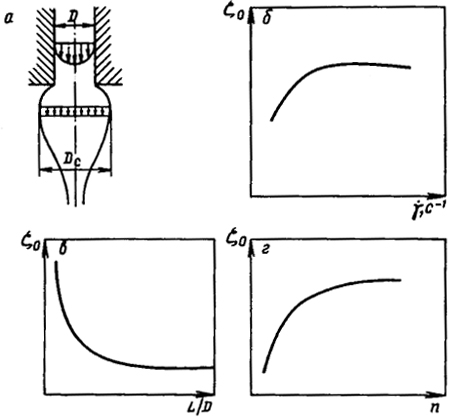
Рис. 4.10. Эффект Барруса:
а - изменение профиля скоростей при выходе жидкости из капилляра; б - влияние градиента скорости сдвига  на ζ1; в - влияние геометрических размеров капилляра на ζ0; г -зависимость ζ0 от индекса течения п
на ζ1; в - влияние геометрических размеров капилляра на ζ0; г -зависимость ζ0 от индекса течения п
- увеличении вязкости среды, в которую экструдируется полимерная жидкость.
Средняя скорость движения струи, в которой полностью завершился процесс релаксации и выравнивания поля скоростей, может быть вычислена по формуле

В сдвиговом поле реализуются достаточно большие высокоэластические деформации, обусловливающие возникновение аксиальных растягивающих напряжений (эффект Вайссенберга). В условиях кругового течения, например в зазоре между коаксиальными цилиндрами, раствор или расплав полимера как бы стягивается силами, возникающими при появлении нормальных напряжений. Они противодействуют как силе тяжести, так и центростремительной силе (рис. 4.11).
Например, если раствор полимера или расплав помещены в зазор между двумя коаксиальными цилиндрами, причем внутренний цилиндр (или стержень) неподвижен, то при вращении внешнего цилиндра жидкость поднимается по стенкам внутреннего неподвижного цилиндра (см. рис. 4.11, а) или по неподвижному стержню (см. рис. 4.11, б). Она может собираться
180
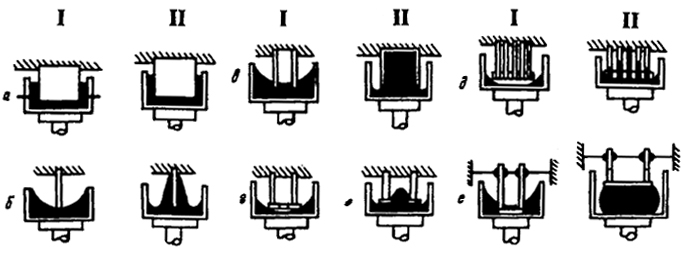
Рис. 4.11. Эффект Вайссенберга:
I - неньютоновские жидкости; II - ньютоновские жидкости. Пояснение в тексте
внутри неподвижной, открытой снизу трубы (см. рис. 4.11, в), подниматься по трубкам, вставленным в неподвижный диск (см. рис. 4.11, д), собираться под невращающимся диском, поднимая его (см. 4.11, е). Подобные эффекты отсутствуют при идентичных условиях деформирования ньютоновских жидкостей (см. рис. 4.11).
Естественно, что величина нормальных напряжений зависит от величины гидростатического давления, а нормальные напряжения проявляются только на периферии струи.
181
