4.3.3. Входовые эффекты
При истечении жидкости из резервуара 1 через трубу (капилляр) 2 (см. рис. 4.5 и 4.8) происходит существенная перестройка структуры потока, связанная с формированием профиля скоростей. При входе в трубу профиль скоростей имеет практически прямоугольную форму ( ≈ 0). Лишь у самой стенки трубы (капилляра) скорость пристенного слоя полимерной жидкости приближается к нулю. Постепенно скорость слоев жидкости, близких к оси трубы (капилляра), возрастает. Такое изменение распределения скоростей по сечению потока продолжается до тех пор, пока профиль скоростей не приобретет формы, соответствующей режиму течения. Для ньютоновских жидкостей эпюра скоростей описывается квадратичной параболой. Для неньютоновских псевдопластичных жидкостей скорость потока в данном случае жидкости связана со средней скоростью течения зависимостью
≈ 0). Лишь у самой стенки трубы (капилляра) скорость пристенного слоя полимерной жидкости приближается к нулю. Постепенно скорость слоев жидкости, близких к оси трубы (капилляра), возрастает. Такое изменение распределения скоростей по сечению потока продолжается до тех пор, пока профиль скоростей не приобретет формы, соответствующей режиму течения. Для ньютоновских жидкостей эпюра скоростей описывается квадратичной параболой. Для неньютоновских псевдопластичных жидкостей скорость потока в данном случае жидкости связана со средней скоростью течения зависимостью

где r - радиус рассматриваемого слоя (расстояние его от оси потока жидкости).
Торможение потока при входе в трубу меньшего диаметра приводит к резкому возрастанию энергозатрат (см. рис. 4.8, б). Они существенно уменьшаются, если входное отверстие оформлено в виде конуса (ас на рис. 4.8, а и кривая 2 на рис. 4.8, б). При этом формирование профиля скоростей происходит более плавно. Естественно, что возникающие в полимерной жидкости перенапряжения релаксируют в процессе течения в трубе (капилляре). Для ньютоновских жидкостей длина участка формирования стабильного профиля скоростей составляет
lвх = (0,05 ÷ 0,16) ReDт,
где Re - критерий Рейнольдса; Dт - диаметр трубы.
Обычно для полимерных жидкостей этот путь значительно больше: lвх ≈ (5 ÷ 12)Dт.
176
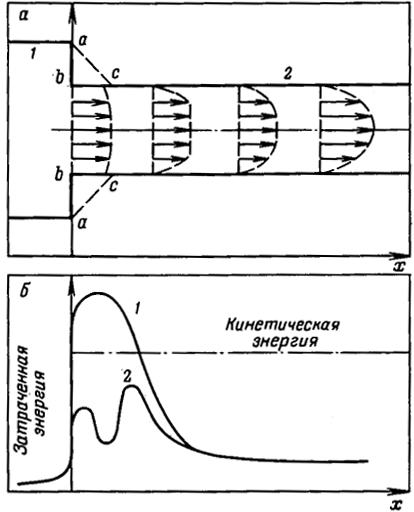
Рис. 4.8. Схема формирования профиля скоростей при течении расплавов и концентрированных растворов полимеров (а) и изменение энергозатрат (б):
а: 1 - резервуар; 2 - труба;
б: 1 - входное отверстие кольцевое (ab); 2 - входное отверстие в виде конуса (ас)
При экструзии концентрированных растворов и расплавов полимеров через капилляры высокоэластическая деформация (см. рис. 3.7) существенно влияет на динамику формирования стабильного профиля скоростей, приводя к росту lвх. Это обусловливает значительную потерю напора уже на входе, ΔРвх. Эти потери напора на входе в трубу (капилляр) могут быть приравнены к дополнительному перепаду давления в гипотетическом капилляре (трубе) такого же диаметра, Dт, как и тот, по которому экструдируется жидкость, но с длиной, большей на mR. В связи с этим суммарное напряжение сдвига τс с учетом входового эффекта может быть вычислено по формуле

Значение т при этом численно равно тангенсу угла наклона прямой, характеризующей зависимость изменения давления вдоль капилляра как функции отношения l/R. Оно равно угловому коэффициенту в уравнении, описывающем эту прямолинейную зависимость: ΔР = а + b · l/R. Величина τс может быть
177
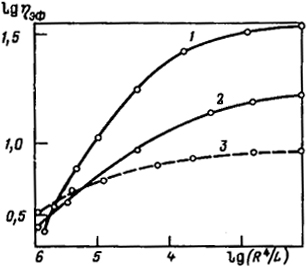
Рис. 4.9. Влияние геометрических размеров капилляров на ηэф некоторых растворов полимеров:
1 - 30%-й (мас.) раствор ХПВХ в ацетоне; 2 - 30%-й (маc.) раствор ХПВХ в ДМФ; 3 - 15%-й (маc.) раствор ПАН в ДМФ
также вычислена по значениям ΔР, на капиллярах различной длины при условии постоянства объемной скорости (расхода) жидкости:
τс = (R/2) [ΔP1 - ΔP2] / (l1 - l2)].
Существенная зависимость вязкостных свойств концентрированных растворов и расплавов полимеров от геометрических размеров капилляров (длины l и радиуса R) иллюстрируется рис. 4.9.
Влияние этого фактора, а также входовых эффектов на энергетический баланс процесса течения псевдопластичных жидкостей весьма существенно. Расход энергии (в 10-7 Дж · с-1)) необходимый для обеспечения постоянной объемной скорости (расхода) Q = 5,09 · 10-10 м3 · с-1 при экструзии через капилляр диаметром 0,03 мм 8%-го раствора целлюлозы в реактиве Швейцера при 303 К, иллюстрируется следующими данными (при lDт, равном 0,5 и 20):
| |
0,5 |
20 |
| Подведенная мощность, необходимая для стабильности Q |
150 |
1823 |
| Затраты: |
|
|
| на формирование профиля скоростей |
3 · 10-5 |
3 · 10-5 |
| на трение |
43 |
1716 |
| на изменение кинетической энергии |
3 · 10-4 |
3 · 10-4 |
| на обратимую деформацию |
107 |
107 |
| в том числе: |
|
|
| рассеяние энергии при релаксации напряжений |
21,5 |
76,6 |
| рассеяние энергии при выходе струи из капилляра |
85,5 |
30,4 |
Таким образом, основными факторами, определяющими величину ΔР, являются: потери на трение, возрастающие с увеличением длины трубы (капилляра) l, и потери на релаксацию
178
деформаций (и напряжений), также повышающиеся при увеличении l. На параметры течения полимеров в вязкотекучем состоянии влияют и "эффекты выхода". Типичной особенностью течения полимеров из капилляра является увеличение диаметра струи по сравнению с диаметром отверстия ("расширение струи").
179
