4.3.2. Реологические уравнения состояния полимеров в условиях вязкого течения

Простейший случай течения псевдопластичной жидкости (расплава или концентрированного раствора полимера) - это стационарный поток со сформировавшимся профилем скоростей. При этом объемный расход жидкости, протекающей через поперечное сечение трубы (или капилляра), составляет

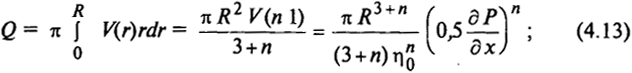
здесь V - линейная скорость жидкости вдоль оси трубы; ∂Р/∂х - потеря напора вдоль оси трубы;

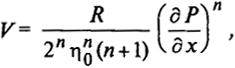
где п - индекс течения.

174

Таблица 4.1. Варианты эмпирического описания реограмм

Для ньютоновской жидкости (n = 1) эпюра скоростей установившегося течения имеет форму параболы второй степени (см. рис. 4.1).

Величина градиента скорости у стенки трубы (капилляра) составляет

R =

Q

πR3

 (n + 3).

В общем случае ∂Р/∂х ≈ ΔP/L, где L_т - длина трубы, а ΔР - разность давлений полимерной жидкости на входе и на выходе из трубы, т.е. ΔР = Р₁ - P₂.

Существующие гипотезы и теории аномалии вязкостных свойств являются в большинстве случаев полуколичественными. В табл. 4.1 приводятся эмпирические формулы, связывающие эффективную вязкость η_эф с τ, , а также с модулем сдвига G.

В приведенных формулах a, b, k, C

0

1

, С

0

2

и v - эмпирические постоянные.

Эти эмпирические формулы удовлетворительно описывают реограммы в диапазоне практически реализуемых τ и .

Определение значений производной d(lg )/d(lg τ) [см. рис. 4.2] позволяет оценить индекс течения п. Наиболее удобно для практических целей реологическое уравнение (4.3). Согласно

175

этому уравнению имеем

lg = n(lgτ- lgη_эф)

Следовательно,

176