4.1.1. Ньютоновские жидкости
Если в процессе деформирования полимерного материала вся энергия приложенного внешнего силового поля диссипирует, то реализуется процесс течения. При этом вся накопленная деформация оказывается необратимой, а достигнутое новое состояние жидкости - равновесным.
В процессе медленного течения под воздействием приложенных к жидкости сил происходит необратимое смещение соседних слоев ее, сопровождающееся преодолением сил, препятствующих сдвигу (рис.4. 1). Этот процесс описывается законом Ньютона
где τ - напряжение сдвига; dε/dt - скорость перемещения слоя жидкости относительно соседнего, находящегося на расстоянии dx; 
- градиент скорости сдвига; η - коэффициент вязкости (вязкость).
Этот закон течения справедлив в условиях ламинарного потока.
162
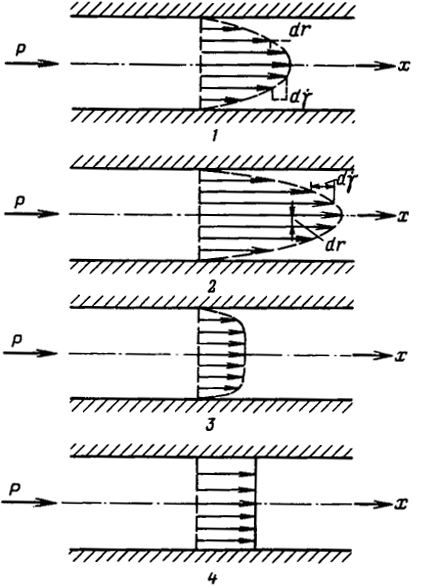
Рис. 4.1. Схемы течения жидкости в трубе (n - индекс течения):
1 - ньютоновская жидкость; 2-4 - неньютоновские жидкости; 2 - п < 1 (псевдопластичная жидкость); 3 - п > 1 (дилатантная жидкость); 4 - п → ∞
В интегральной форме он описывается уравнением Гагена - Пуазейля
где r и l - радиус и длина трубы (капилляра), по которой течет жидкость; ΔР - перепад давления на входе и выходе жидкости из трубы (капилляра); Q - объемная скорость жидкости; t - время истечения жидкости.
Сопоставление уравнений (4.1) и (4.2) показывает, что
τ = ΔР · r/(2l) и = 4Q/(πr3).
Распределение скоростей соседних гипотетических слоев в ньютоновской жидкости при установившемся потоке описывается квадратичной параболической зависимостью (см. рис. 4.1). Течение ньютоновских жидкостей характеризуется независимостью вязкости от напряжения сдвига т, скорости V = dε/dt
163
и скорости сдвига . Такое сдвиговое течение характерно для многих низкомолекулярных веществ, находящихся в жидком агрегатном состоянии.
164
