2.4.1. Тэта-состояние растворов полимеров
Возможности приобретения макромолекулой, находящейся в растворе, наиболее вероятных конформаций могут быть реализованы лишь в том случае, если этому не будут препятствовать другие полимерные цепи.
Растворы полимеров, в которых взаимодействием сольватированных полимерных цепей можно пренебречь, называются разбавленными. На рис. 2.4 приведена схема, иллюстрирующая возможность конформационных переходов макромолекул в растворе; размеры звеньев и молекул растворителя условно приняты одинаковыми. Изменение конформаций полимерной цепи становится возможным в том случае, когда имеется соответствующая "дырка" в структуре растворителя, находящаяся в пределах досягаемости звена полимера.
Движение молекул растворителя в системе полимер - растворитель также определяется наличием таких пустот, "дырок".
При случайных сближениях двух полимерных цепей звенья одной из них препятствуют звеньям другой проникать в занимаемую ими область раствора. Объем, который занят молекулярным клубком, образованным одной полимерной цепью не может быть занят другим и называется исключенным. Этот постулат относится и к отдельным сегментам.
Для свободносочлененной цепи справедливо уравнение
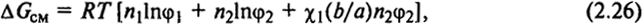
где b/а - отношение короткой и длинной осей макромолекулярного клубка (степень асимметрии полимерной цепи в разбавленном растворе); χ1 - параметр взаимодействия полимер - растворитель (константа Флори); п1, φ1 и n2, φ2 - число молей и объемная доля растворителя и полимера в растворе соответственно.
101

Рис. 2.4. Схема строения разбавленного раствора полимера; штриховыми кружками показаны "дырки"
Так как ∂Gсм/∂ni = μi - μ
= Δμ
i, то уменьшение химического потенциала растворителя в растворе по сравнению с его величиной для чистого растворителя составляет
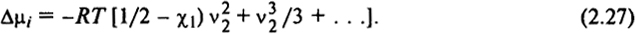
Пусть
=
k1,
= ψ и θ =
T;
тогда

В термодинамически плохом растворителе значения ΔHсм и θ велики, т.е. раствор полимера тогда устойчив, когда θ/T < 1.
В термодинамически хороших растворителях ΔHсм и θ сравнительно малы. Вследствие этого при понижении температуры растворы замерзают раньше, чем достигается условие Т = θ. Так как при Т = θ согласно уравнением (2.27) и (2.28) k1 = ψ1, то 1/2 - χ1 = 0. Следовательно, при θ-температуре χ1 = 0,5. В этих условиях макромолекулы при случайных столкновениях не взаимодействуют.
Таким образом, тэта-состояние (при θ-температуре или в θ-растворителе) соответствует состоянию идеального раствора. На фазовых диаграммах (см. рис. 2.3) ВКТР соответствует θ-температуре раствора с бесконечно большой молекулярной массой.
Определить θ-температуру методом анализа фазового равновесия можно, оценив температуру распада Т0 для нескольких концентраций фракций полимера определенной молекулярной массы Mп, используя уравнение Флори
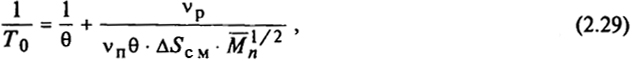
где vп и vp - парциальные удельные объемы полимера и растворителя соответственно; ΔSсм - энтропия растворения (смешения).
102
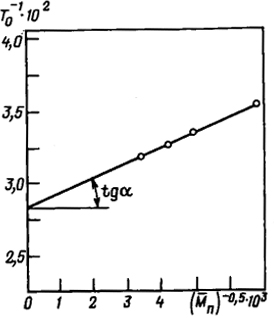
Рис. 2.5. Влияние молекулярной массы полимера на температуру фазового распада раствора Тo
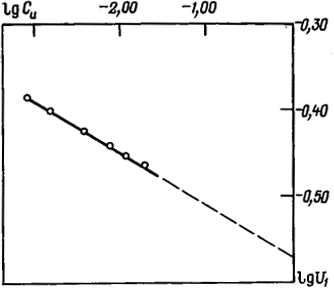
Рис. 2.6. Логарифмическая зависимость концентрации полимера в точке помутнения Си от соотношения растворителя и осадителя U1
Задача. При определении θ-температуры системы полистирол - циклогексан методом фазового равновесия были получены следующие результаты:
| Мn |
20000 |
35000 |
56000 |
82000 |
| ВКТР,°С |
28,4 |
29,8 |
30,5 |
31,8 |
Определить θ-температуру системы.
Решение. Уравнение (2.29) описывает прямую в координатах T - M (рис. 2.5).
Пересчет приведенных экспериментальных величин дан ниже:
| М ·103 |
7,00 |
5,00 |
4,22 |
3,49 |
| 1/T0·102 |
3,52 |
3,35 |
3,25 |
3,14 |
Экстраполяция М → 0 приводит к 1/θ = 2,89·10-2. На этом графике tgα = vp/(vпθ·ΔSсм). Следовательно, θ-температура для этой системы равна 34,6°С.
Такой метод оценки θ-температуры используется для систем полимер - растворитель, которые способны распадаться при осаждении на две фазы.
Тэта-состояние раствора может быть также оценено по результатам определения "чисел осаждения" (по определению точки помутнения), используя метод турбидиметрического титрования. Он основан на титровании осадителем растворов фракций полимера различной концентрации до помутнения. На основании полученных результатов строят графики зависимости
103
(в логарифмических координатах) добавки осадителя от концентрации полимера и экстраполируют прямую на 100%-й полимер (рис. 2.6). Соотношение растворителя и осадителя в этой точке соответствует θ-состоянию полимера. Важным преимуществом этого метода является малая зависимость результатов от молекулярной массы высокомолекулярного соединения.
Задача. При турбидиметрическом титровании при 20°С 100 см3 раствора полиметилметакрилата (ПММА) в бензоле н-гептаном были получены следующие результаты:
| Концентрация ПММА, % (мас.). |
0,1 |
0,5 |
1,0 |
1,5 |
| Количество н-гептана, см3 |
55,0 |
50,3 |
47,8 |
46,5 |
Определить соотношение бензола и н-гептана в θ-точке.
Решение. Определяем концентрацию полимера в точке помутнения (Си). Если исходная концентрация раствора 0,1% (мас.), то
Си = 0,1/(100ρ1 + 55,0ρ2),
где ρ1 и ρ2 - плотности бензола и н-гептана (879 и 660 кг/м3 соответственно);
Си = 0,1/(100·0,879 + 55,0·0,660) = 8,05·10-4.
Тогда соотношение осадителя и растворителя в этой смеси составит
U1 = 55,0·0,660/[(100 - 0,1)0,879] = 0,413.
Результаты аналогичных расчетов для других концентраций сведены в следующую таблицу.
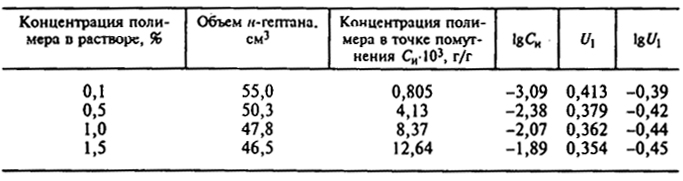
Строим график зависимости lgCи в точке помутнения от lgU1 (рис. 2.6). Экстраполируя полученную прямую до lgCи = 0, т.е. на 100%-ю концентрацию полимера, получаем на оси ординат отрезок (lgU1)C=100 = -0,56. Следовательно, соотношение н-гептана и бензола в θ-растворителе равно 0,275, т.е. 0,275:1 (мас.).
Значения θ-температур для различных систем полимер - растворитель могут быть определены также по изменению угла наклона линейной зависимости плотности и показателя преломления растворов полимеров от температуры.
104
Значения θ-температур для некоторых систем приведены ниже:
| Полимер |
Растворитель |
θ-температура, К |
| Амилоза |
0,33 н. раствор КСl в воде |
298 |
| Ацетилцеллюлоза (57,3% связанной СН3СООН) |
Ацетон |
310 |
| Триацетилцеллюлоза (61,2% связанной СН3СООН) |
Бензиловый спирт |
376 |
| Поливинилхлорид |
ДМФ |
309,5 |
Однако уравнение (2.26) справедливо при b/а → 1, т.е. в случае, когда макромолекула моделируется идеально гибкой цепью.
Если же макромолекула волокнообразующего полимера характеризуется ограниченной гибкостью (например, целлюлоза и ее эфиры, полиакрилонитрил, поли-n-фенилентерефталамид и др.), то уравнение (2.12) должно быть записано в виде

где ΔSоб = ΔSсм + ΔSд (здесь ΔSоб - общая энтропия; ΔSсм - изменение энтропии в результате смешения полимера и растворителя, ΔSд - энтропия дезориентации макромолекул).
В этом случае
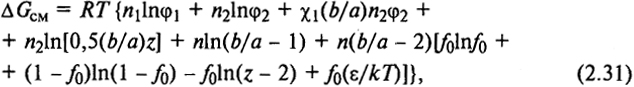
где z - координационное число "квазирешетки" раствора; f0 - параметр гибкости полимерной цепи; ε - энергетический параметр, характеризующий вероятность образования предельно распрямленных макромолекул, т.е. это величина, функционально связанная с U0; k - константа Больцмана; Т - температура, К.
Параметр гибкости полимерной цепи f0 может быть математически описан с использованием следующей модели (см. рис. 2.4).
Представим раствор полимера как некоторую регулярную систему в виде лабильной решетки с координационным числом z. Состоит такая "квазирешетка" из п ячеек.
Пусть одна из z - 1 доступных для полимерной цепи ячеек, заполнение которой i-м сегментом макромолекулы не препятствует образованию предельно вытянутой конформации цепи (т.е. палочкообразной форме ее), характеризуется энергией, которая на величину е меньше остальных z - 2 ячеек. Тогда равновесная
105
гибкость макромолекул f0 определяется из условия
= 0.
Следовательно, исходя из уравнения (2.31), получаем, что
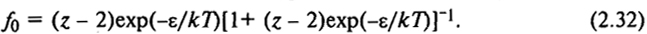
Очевидно, что f0 не зависит от концентрации полимера в растворе. Для оценки f0 могут служить все методы определения размеров цепей, в том числе и (h)1/2, характеризующий скелетную гибкость. Пороговое значение f0 = 0,63: все полимеры, макромолекулы которых характеризуются f0 > 0,63, относятся к гибкоцепным, a f0 < 0,63 - к жесткоцепным.
106
