Среднестатистический сегмент Куна
Свободное вращение звеньев вокруг валентных связей ограничивается взаимодействием функциональных групп, входящих в состав этих звеньев. Интенсивность такого ограничения свободного вращения звеньев характеризуется величиной потенциального барьера U0. Значения U0 пропорциональны kT, где k - константа Больцмана. Если U0 << kT, то гибкость макромолекулы оказывается близкой к идеальной. Для многих волокнообразующих полимеров U0 < kT. Если же U0 >> kT, то полимерная цепь обретает форму жесткого стержня.
Для характеристики гибкости реальных макромолекул часто используют понятие "статистического сегмента".
Сущность этого понятия заключается в следующем. Вращение отдельных групп и звеньев в полимерной цепи не свободно, а заторможенно. Можно представить себе такую модель полимерной цепи, в которой ее отдельные участки, состоящие из нескольких звеньев, могли бы свободно вращаться. Очевидно, что величина такого участка будет больше, чём размер реального звена. Однако в обоих случаях число возможных конформаций макромолекул будет одинаковым. Иными словами, для удобства математического описания гибкости макромолекулы реальная полимерная цепь с заторможенным вращением звеньев заменяется гипотетической моделью, способной принимать такое же количество конформаций, что и реальная цепь, но построенной из свободносочлененных жестких участков - сегментов.
Таким образом, статистический сегмент Куна - это математическая абстракция, мера гибкости макромолекул, введенная для описания физических свойств полимеров законами идеальных систем.
Очевидно, чем жестче макромолекула, тем больше размер сегмента. Предельно жесткая макромолекула представляет собой один сегмент, который включает в себя все звенья полимерной цепи. Если в результате элементарного акта теплового движения в перемещении участвуют nK звеньев цепи макромолекулы,
85
причем nK < Р, то размер сегмента Куна будет определяться соотношением

где δ - угол, дополнительный к валентному (см. рис. 2.2, а).
Пусть длина выпрямленной без нарушений валентных углов макромолекулы L ("контурная" длина) составляет

Тогда макромолекула, состоящая из Р звеньев, может быть представлена как цепь, образованная L/LK = т сегментами. Значение т должно быть не менее 10.
Легко показать, что

Для карбоцепных полимеров для модели свободносочлененной цепи имеем
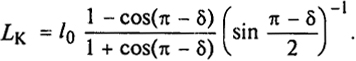
Таблица 2.1. Характеристика термодинамической гибкости некоторых полимеров

86
Задача. Вычислить размер сегмента Куна при заданном значении l0 для полиметиленовой цепи.
Решение. Для углеводородных цепей с тетраэдрическими связями С-С валентный угол равен 109°28'.
Поэтому sin[(π - δ)/2] = 0,816 и LK = 2,45l0.
Сравнительная характеристика гибкости некоторых волокнообразующих полимеров приведена в табл. 2.1.
87
