Физико-механические свойства материалов зависят не только от средней молекулярной массы, но и от вида распределения полимерных цепей по молекулярным массам. При одном и том же значении средней молекулярной массы комплекс эксплуатационных свойств полимера тем лучше, чем уже распределение по молекулярным массам, т.е. чем больше доля полимерных цепей, приближающихся по длине к среднему значению.
Теоретические функции распределения по молекулярным массам можно вывести из кинетики реакций синтеза полимера при определенном механизме процесса. Однако различные побочные процессы, протекающие как при синтезе, так и при выделении полимера из реакционной смеси, часто существенно
56
изменяют полидисперсность, характер молекулярно-массового распределения (ММР).
Изучение ММР осуществляют путем фракционирования полимера подходящим способом, главным образом - методами дробного растворения и осаждения. При добавлении к раствору полимера значительных количеств осадителя или при охлаждении происходит осаждение части полимера. Условием равновесия между двумя фазами в бинарной системе является равенство химических потенциалов в обеих фазах (см. гл. 2). Температура, при которой происходит разделение фаз (Tр), определяется упрощенным уравнением

где κ - постоянная для данной системы полимер - растворитель; θ - тета-температура.
Разделение полимера на фракции изменением температуры получило название термоградиентного метода фракционирования.
Следовательно, θ-температура является температурой фракционирования, при которой начинается растворение (или осаждение) полимера с бесконечно большой молекулярной массой.
Задача. Вычислить значение θ-температуры для 0,5%-го раствора перхлорвинила в смеси дихлорэтан - бутиловый спирт (60:40), если в результате применения термоградиентного метода фракционирования были получены следующие результаты:
| Выход фракции, % |
6,4 |
4,5 |
6,9 |
16,4 |
21,3 |
14,4 |
27,0 |
3,1 |
| Температура,°С |
6,3 |
16,8 |
21,1 |
28,2 |
31,8 |
35,6 |
37,6 |
41,4 |
| Mi·104 |
0,438 |
0,820 |
1,070 |
1,843 |
2,590 |
4,410 |
6,280 |
9,260 |
Решение. Построим график зависимости Т от M (рис. 1.21). Отрезок, отсекаемый прямой на оси ординат, соответствует θ-температуре, равной 324,7 К.
При разделении раствора на фазы в результате осаждения полимера изменение химического потенциала макромолекул с молекулярной массой Мi описывается упрощенным уравнением
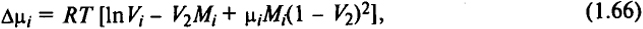
где Vi - мольный объем фракции полимера с молекулярной массой Мi; V2 = Vi.
При выпадении фракции полимера в осадок происходит некоторое уплотнение полимера, т.е. V
≠
Vi, где
V - мольный
57
![Рис. 1.21. Зависимость для 0,5%-х растворов перхлорвинила в смеси дихлорэтан - бутанол [8:2 (об.)]](img/B1223p58-a1.jpg)
Рис. 1.21. Зависимость T
=
f(
M) для 0,5%-х растворов перхлорвинила в смеси дихлорэтан - бутанол [8:2 (об.)]
объем полимера, выпавшего в осадок. В условиях равновесия

где φ - параметр распределения макромолекул полимера между раствором и осадком.
Для всех значений Мi имеем V
>
Vi, т.е. в осадке находятся молекулы любого размера. Следовательно, часть молекул всех размеров всегда присутствует как в растворе, так и в осадке. Доли молекул с
Мi, оставшихся в растворе (ψ
i) и выпавших в осадок (1 - ψ
i), можно выразить следующим образом:
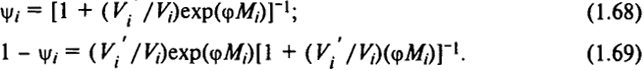
Эффективное фракционирование полимера можно проводить лишь из разбавленных растворов.
Теоретические функции распределения по молекулярным массам с экспериментальными данными, получаемыми при фракционировании полимеров, удобно сравнивать графически. Определяя массы фракций и их средние молекулярные массы, строят интегральную кривую распределения по молекулярным массам, т.е. кривую зависимости суммарной массы всех фракций от молекулярной массы. Диаграмму распределения по молекулярным массам в виде непрерывной кривой R = f(M) можно построить лишь в тех случаях, когда охватывается достаточно широкий диапазон молекулярных масс. Обычно такая кривая имеет S-образную форму.
Если в результате фракционирования было выделено i фракций, то ордината интегральной кривой распределения по молекулярной
58
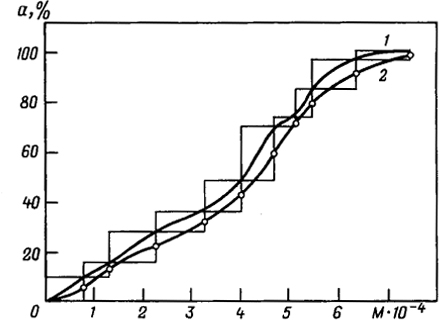
Рис. 1.22. Интегральная кривая молекулярно-массового распределения, построенная:
1 - по экспериментальным точкам; 2 - через "середины ординат"
массе составит
a1 + а2 + а3 + ... + ai = 1, т.е.
ai = 100%.
Это обстоятельство позволяет допустить построение интегральной кривой по числу точек, равному числу фракций.
Обычно применяют два метода построения интегральных кривых ММР - по экспериментальным точкам и по способу "средних точек".
Задача. Построить интегральную кривую ММР по экспериментальным точкам, если при фракционировании перхлорвинила из 1%-го раствора в ацетоне осаждением метиловым спиртом получены следующие фракции:
| аi, % |
10 |
12 |
8 |
11 |
18 |
7 |
12 |
9 |
10 |
3 |
| Mi·104 |
7,5 |
6,2 |
5,4 |
5,0 |
4,6 |
3,9 |
3,3 |
2,5 |
1,2 |
0,6 |
Решение. Строим график зависимости ai от Mi (рис. 1.22). Построение начинаем с фракции с меньшей молекулярной массой.
Способ "средних точек" основан на довольно грубом допущении, что каждая фракция полимера содержит молекулы с молекулярной массой как большей, чем средняя молекулярная масса предыдущей фракции, так и с меньшей. Ординаты средних точек при таком способе построения находят по формуле
a
=
+
aj,
где a - "исправленная" массовая доля i-й фракции; aj - сумма массовых долей всех предыдущих фракций.
59
Задача. Используя данные предыдущей задачи, построить интегральную кривую молекулярно-массового распределения, учитывая "исправленную" массовую долю i-й фракции.
Решение. В этом случае построение может быть осуществлено двумя способами: либо следует провести кривую через середины массовых долей (см. рис. 1.22), либо необходимо предварительно рассчитать ординаты точек, т.е. оценить "исправленную" интегральную функцию для каждой фракции. Для данного примера
a = a1/2 = 3/2 = 1,5; а = a2/2 + a1 = 8, и т.д.
| а |
1,5 |
8 |
17,5 |
28 |
37,5 |
50 |
64,5 |
74 |
84 |
95 |
| Мi·104 |
0,6 |
1,2 |
2,5 |
3,3 |
3,9 |
4,6 |
5,0 |
5,4 |
6,2 |
7,5 |
Интегральная кривая ММР не дает наглядного представления о распределении полимерных молекул по длине. Дифференциальная кривая ММР лишена этого недостатка. Наилучший способ ее построения - метод графического дифференцирования (несмотря на то, что даже в случае получения очень большого числа фракций данные фракционирования являются приближенными).
Метод графического дифференцирования состоит в следующем. Из выбранных для дифференцирования точек на интегральной кривой опускают перпендикуляры на ось абсцисс и через каждую точку проводят прямую, параллельную оси абсцисс, до пересечения с ординатой предыдущей точки. Отношение величины отрезка ординаты к величине отрезка абсциссы, образующих стороны каждого из полученных треугольников, умноженное на масштаб, дает значение Δa/ΔM (рис. 1.23).
Для превращения экспериментальной ступенчатой диаграммы дифференциального распределения в непрерывную кривую R = da/dM = f(M) предполагается, что распределение описывается непрерывной функцией. При графическом дифференцировании получается непрерывная кривая "идеального фракционирования". Следует учитывать, что экспериментальные ошибки, проявляющиеся в разбросе точек на интегральной кривой, становятся более заметными в процессе дифференцирования. Однако практически существенны только основные характеристики дифференциальной кривой: база и положение пика (или пиков).
Рассмотрим два крайних случая. Когда полимер состоит из макромолекул равной длины, дифференциальная кривая "вырождается" в прямую, параллельную оси R. При максимальной же полидисперсности образца полимера площадь, отсекаемая кривой R = f(M), имеет форму прямоугольника. Отсутствие разрывов на кривых R = f(M) означает, что в системе
60
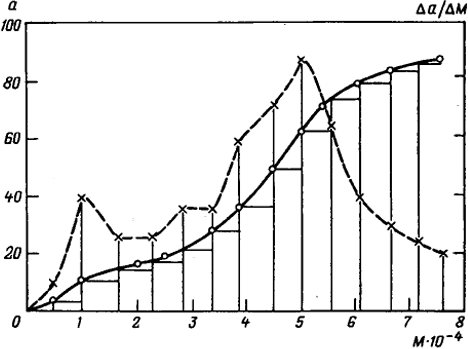
Рис. 1. 23. Интегральная (-) и дифференциальная (- - - -) кривые молекулярно-массового распределения. Интегральная кривая построена по экспериментальным точкам
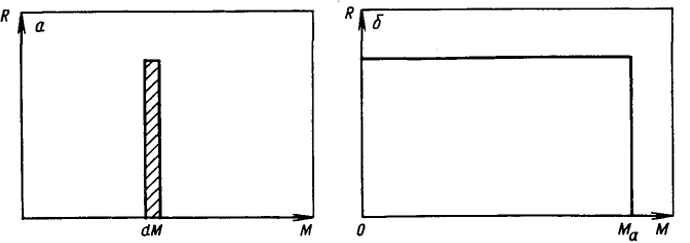
Рис. 1.24. Схема распределения по молекулярным массам монодисперсного (а) и максимально полидисперсного (б) полимеров
имеются все фракции с молекулярной массой до Ма включительно (рис. 1.24).
При наличии экстремумов на дифференциальной кривой ММР система приближается к первому крайнему случаю - к максимальной однородности. Наоборот, выпрямление кривой, наличие участков, приближающихся к параллельным относительно оси М, соответствует увеличению степени полидисперсности.
Во всех случаях площадь под интегральной кривой соответствует М·100, а под дифференциальной кривой - 100, если масса фракций аi выражена в % от взятой навески.
Задача. Проверить правильность фракционирования хлорированного поливинилхлорида (см. задачу на с. 59), если средневязкостная молекулярная масса составляет 40000.
61
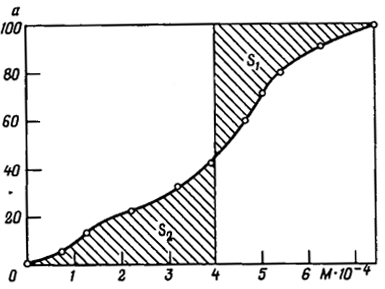
Рис. 1.25. Схема графической проверки правильности фракционирования
Решение. Правильность фракционирования можно проверить следующим образом. На интегральной кривой (рис. 1.25) через точку, соответствующую средней молекулярной массе полимера, восставляют перпендикуляр к оси абсцисс и определяют площадь, ограниченную осью абсцисс, перпендикуляром и частью интегральной кривой, находящейся слева от перпендикуляра (S2), и площадь, ограниченную продолжением перпендикуляра, интегральной кривой справа от него и горизонтальной прямой, параллельной оси абсцисс и проходящей через а = 100 (S1). Если фракционирование проведено правильно, а молекулярно-массовое распределение подчиняется закону Гаусса, то эти площади равны. Оказалось, что контролируемые площади S1 = 15,4 см2, а S2 = 15,9 см2. Значения S1 и S2 близки.
Площади можно также оценить, сравнивая массу снятых на кальку участков кривой. В рассматриваемом случае оказалось, что масса А1 = 0,0556 г, а A2 = 0,0570 г, что также можно считать удовлетворительным совпадением.
Количественная оценка степени полидисперсности. Полидисперсность полимера характеризуют степенью неоднородности (по Шульцу) U.

Очевидно, что для монодисперсного продукта Мw = Мn и U = 0.
Задача. Рассчитать полидисперсность по Шульцу для задачи на с. 59.
Решение. По формулам (1.2) и (1.3) рассчитываем среднечисленную и средневзвешенную молекулярные массы:
Мn = 3,38·104; Мw = 4,334·104.
Вычисляем полидисперсность по формуле (1.70):
U = Мw/Mn - 1 = 0,28.
Количественное сопоставление различных дифференциальных кривых ММР для полимеров одного химического состава может быть проведено сопоставлением степеней однородности
62
Π, определяемых по формуле Геллера-Мескина

где П - степень однородности; n - число ступеней дифференцирования; R - высота перпендикуляра от абсциссы до точки пересечения с дифференциальной кривой на каждой ступени графического дифференцирования (см. рис. 1.23).
Отношение П к Мw дает приведенную степень однородности Sп:

Задача. Из решения задачи на с. 59 рассчитать приведенную степень однородности.
Решение. Измеряем R в каждой ступени дифференцирования (см. рис. 1.23):
| Ступень |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| R |
9 |
39 |
24 |
24 |
36 |
36 |
60 |
72 |
90 |
66 |
42 |
30 |
24 |
20 |
| n = 14 |
|
|
|
|
|
|
| �
|
|
| �
|
| �
|
|
Вычисляем степень однородности по формуле (1.71):
П = 0,98.
По формуле (1.72) находим приведенную степень однородности, учитывая, что Мw = 4,334·104 (см. предыдущую задачу):
Sп = 0,98/(4,334·104) = 2,26·10-5.
Абсолютные значения приведенной степени однородности для одного полимера существенного интереса не представляют. Однако, если сравнивать значения Sп различных образцов одного и того же полимера, то оказывается, что чем ниже приведенная степень однородности, тем равномернее полимер по своему молекулярному составу. На рис. 1.26 приведены результаты изучения влияния полидисперсности на физико-механические свойства различных волокон. Уменьшение содержания низкомолекулярных фракций в полимере улучшает комплекс физико-механических свойств формуемых из них волокон. Содержание этих фракций не должно превышать 3-5%. С увеличением гибкости полимерных цепей влияние молекулярной однородности полимера на физико-механические свойства волокон и пленок возрастает. Увеличение полидисперсности сравнительно гибко-цепных полимеров приводит к резкому ухудшению прочностных, и в особенности усталостных, характеристик волокон. С повышением жесткости макромолекул волокнообразующих полимеров
63

Рис. 1.26. Влияние приведенной степени однородности Sn на физико-механические показатели поливинилхлоридного, полиакрилонитрильного и ацетатного волокон:
1 - прочность ацетатного волокна; 2 - прочность поливинилхлоридного волокна; 3 - устойчивость к многократным деформациям поливинилхлоридного волокна; 4 - удлинение полиакрилонитрильного волокна; 5 - прочность полиакрилонитрильного волокна; σ - прочность, ε - удлинение, х - число двойных изгибов
влияние формы высокомолекулярной части ММР на механические свойства волокон проявляется в меньшей мере.
Вопрос. Почему волокна и пленки на основе полимеров с более широким ММР обладают меньшей прочностью, хотя степень ориентации структурных элементов в них может быть одинаковой?
Ответ. Прочность на разрыв, а также усталостные характеристики волокон и пленок при одинаковой степени ориентации определяются количеством слабых мест в полимерном материале. На молекулярном уровне такими дефектами являются контакты между концами макромолекул. С увеличением полидисперсности (при одинаковой средней степени полимеризации) количество слабых мест в изделиях увеличивается, что и влечет за собой ухудшение механических характеристик.
64
